Моделирование движения аэрозольной частицы в воздухе при наличии сопротивления

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ  УНИВЕРСИТЕТ

Индивидуальное задание по дисциплине

«Математическое моделирование физических процессов»
Моделирование движения тела в среде при наличии сопротивления

Факультет: ЛА

Группа: МБ-81

Студент: Бобыкина А.А.

Преподаватель: Ивания С.П.

НОВОСИБИРСК

2010 г.

Постановка задачи:

Промоделировать падение аэрозольной частицы в воздухе с высоты  H= 150 м, если сила сопротивления воздуха пропорциональна скорости (использовать формулу Стокса), радиус частицы R = 100 мкм, плотность материала частицы r = 2,5 10³ кг/м³.

1.Определить время падения частицы с высоты Н.

2.Построить зависимость скорости от времени V(t).

Описать математическую модель, алгоритм численного решения, программу. Провести анализ результатов.

Математическая модель

При падении на аэрозольную частицу будут действовать две силы: сила тяжести и сила сопротивления:

ma=F_тяж-F_сопр

Т.к. сила тяжести равна mg, а сила сопротивления, по формуле Стокса: 6πμrv, для ламинарного потока и 6πμrv² для турбулентного.

Поделим обе части уравнения на массу.

Тогда уравнение примет вид:

a=g-(6πμrv)/m (для ламинарного потока)

a=(g-6πμrv²)/m (для турбулентного потока)

Зная, что радиус падающей частицы порядка 10^-4, можно исключить уравнение для турбулентного потока, т.к. коэффициент Рейнольдса мал.

Известные нам величины:

μ=1,82*10⁵  кг/м

ρ=2,5*10³ кг/м³

r=10^-4 м

Выразим массу частицы через известные величины: m=4/3*πr³ρ

a= g-(18πμrv)/(4πr³ρ)=g-(9*μv)/(2r²ρ)                     (1)

Определим порядки ускорения, для этого подставим в уравнение известные величины:

a= 9,8-(9*1,82*10^-5)/(2*10^-8*2,5*10³)v=9,8-(9*1,82)/(2*1*2,5)v;

Сокращая порядки, приходим к выводу, что в  расчетах, величины можно представить как:

μ=1,82

ρ=2,5

r=1

Итого, имеется два дифференциальных уравнения:

dv/dt= a, где a значения  формулы (1)

dy/dt=v;

Начальные условия:

v_|t=0 = 0;

y_|t=0 = 0;
Алгоритм численного решения

Разобьем область изменения переменной t на N интервалов с шагом Dt и заменим в уравнениях дифференциальные выражения их конечно-разностными приближениями, после чего получим итерационные формулы для скорости в точке сетки:

v_i+1=v_i+a_i*dt, где a_i=g-(9*μv)/(2r²ρ)                    

y_i+1=y_i+v_i*dt

Теперь напишем программу, которая будет выводить результат в формат *.csv, чтобы в дальнейшем в Excel можно было построить график.

Текстпрограммы

program aero;

uses crt;

const{Запишем в константы величины с которыми мы будем работать}

m=1.82;        { μ }

ro=2.5;          { ρ }

r=1;                {Радиус}

g=9.8;                        {Ускорение свободного падения}

y0=0;             {Начальные условия}

v0=0;

h=150;           {Высота}

dt=0.1;          {Изменение времени}

var

a,v,y,t: real;

f:text;

begin

clrscr;

y:=y0;             {Присваиваем начальные условия переменным}

v:=v0;

assign(f,'result.csv');         {Открываем файл для записи}

rewrite(f);

repeat

v:=v+(g-(9*m*v)/(2*r*r*ro))*dt; {Применяем метод Эйлера}

y:=y+v*dt;

t:=t+dt;

Writeln('t=',t:0:2,'   y=',y:0:2,'      v=',v:0:2);  {Выводим значения на экран}

Write (f,t:0:2);                                                        {И записываем в файл}

Write(f,'; ');

Writeln(f,v:0:2);

until (y>=h);   {Цикл продолжается пока значения координаты y}

close(f);          {не будет больше или равно высоте}

readln;           

end.

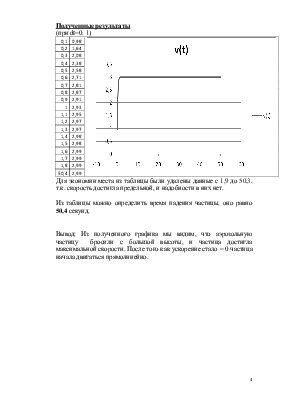
Полученные результаты

(при dt=0. 1)

0,1	0,98
0,2	1,64
0,3	2,08
0,4	2,38
0,5	2,58
0,6	2,71
0,7	2,81
0,8	2,87
0,9	2,91
1	2,93
1,1	2,95
1,2	2,97
1,3	2,97
1,4	2,98
1,5	2,98
1,6	2,99
1,7	2,99
1,8	2,99
50,4	2,99

Для экономии места из таблицы были удалены данные с 1,9 до 50,3, т.к. скорость достигла предельной, и надобности в них нет.

Из таблицы можно определить время падения частицы, оно равно 50,4 секунд.

Вывод: Из полученного графика мы видим, что аэрозольную частицу  бросили с большой высоты, и частица достигла максимальной скорости. После того как ускорение стало = 0 частица начала двигаться прямолинейно.