Передатчик системы безшнурового телефона (выходная мощность – 0,162 Вт; рабочая частот – 1893,8 МГц)

пределах 10 раз на частоте порядка 2 ГГц, зададимся коэффициентом усиления для оконечного каскада К_рОК = 8. Для варакторных умножителей частоты коэффициенты полезного действия имеют следующие значения: η_3f ≈ 0,4 – для умножителя на 3, и  η_4f ≈ 0,3 – для умножителя на 4. Исходя из этого, оценим мощности на входе оконечного каскада , на входах третьего и второго умножителей частоты , .

;                                         (3.2)

 Вт;

;                                           (3.3)

 Вт;

;                                            (3.4)

Вт;

Для дальнейшего построения функциональной схемы необходимо рассмотреть некоторые особенности проектируемого передатчика. Проектируемый передатчик использует гауссовскую частотную модуляцию с минимальным сдвигом (ГЧММС).

Существует два способа формирования сигнала с ГЧММС. Первый основан на использовании частотной манипуляции, второй – квадратурной фазовой модуляции.

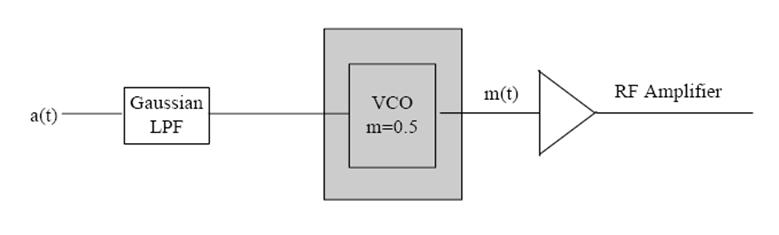
Рис. 3.1. Формирование ГЧММС на основе ЧМ

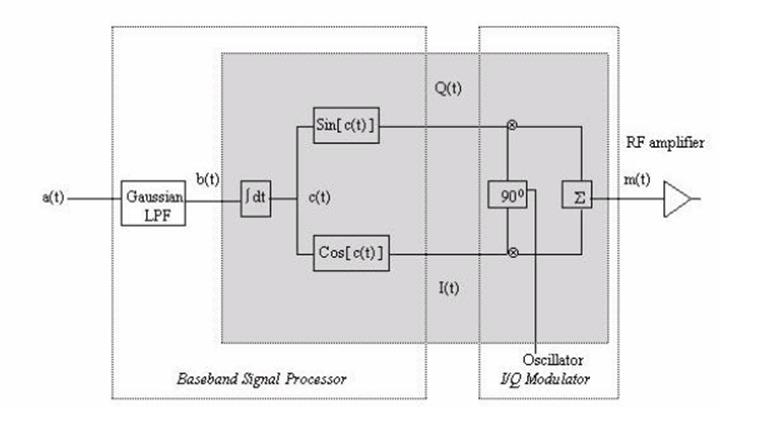
Рис. 3.2. Формирование ГЧММС на основе квадратурной фазовой модуляции

Формирование ГЧММС на основе ЧМ имеет наряду с простотой имеет существенный недостаток, заключающийся в требовании высокой стабильности частоты, которая трудно достигается из-за температурной зависимости параметров автогенератора. В связи с этим метод формирования ГЧММС на основе квадратурной фазовой модуляции является более предпочтительным.

Рассмотрим основные принципы работы этого метода.

Импульсная характеристика гауссовского фильтра описывается следующим уравнением:

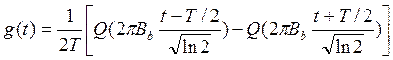                              ,                 (3.5)

для 0 ≤ B_bТ ≤ ∞

где 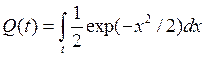                                                ,                                   (3.6)

B_b – полоса пропускания гауссовского фильтра,

Т – длительность бита информации,

B_N=B_bТ –  нормализованная полоса пропускания.

Например, для фильтра с полосой пропускания B_b=1000 и длительностью бита Т=1/2000,  нормализованная полоса пропускания B_N=B_bТ=0,5.

В зависимости от значения B_N импульсная характеристика гауссовского фильтра становиться усеченной и масштабируемой, и чтобы гарантировать этот эффект от прохождения сигнала через фильтр, есть сдвиг на 90˚.

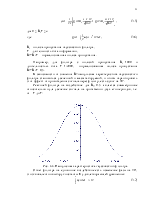
Реакцией фильтра на воздействие для B_N=0.5  является симметричное относительно нуля усечение сигнала на протяжении двух его периодов, т.е. от – Т до Т:

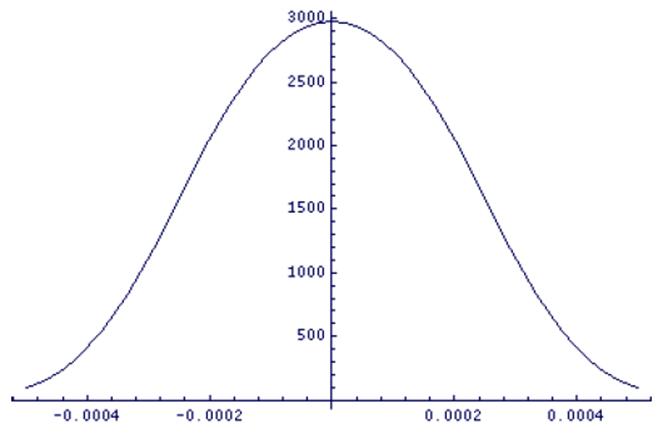
Рис. 3.3. Импульсная характеристика гауссовского фильтра.

Ответ фильтра на единичное воздействие есть изменение фазы на 90˚, это эквивалентно выбору константы К удовлетворяющей уравнению:

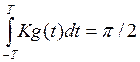                                             (3.7)

Продемонстрируем модуляцию. Для этого воспользуемся случайной бинарной последовательностью a(t), период повторения которой равен 12 бит:

             (3.8)

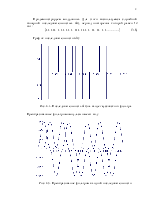
График последовательности a(t):

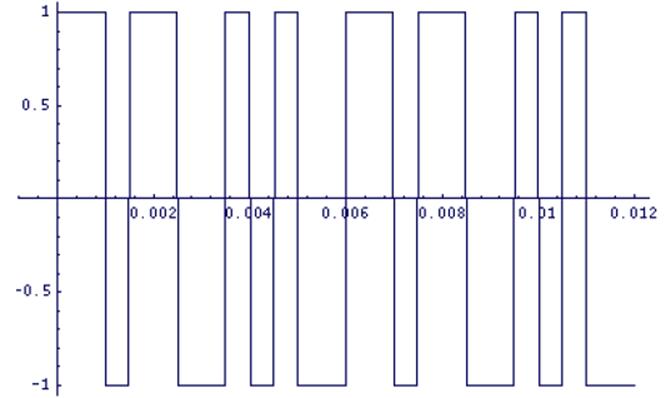
Рис. 3.4. Последовательность a(t) на входе гауссовского фильтра

Преобразованные фильтром импульсы имеют вид:

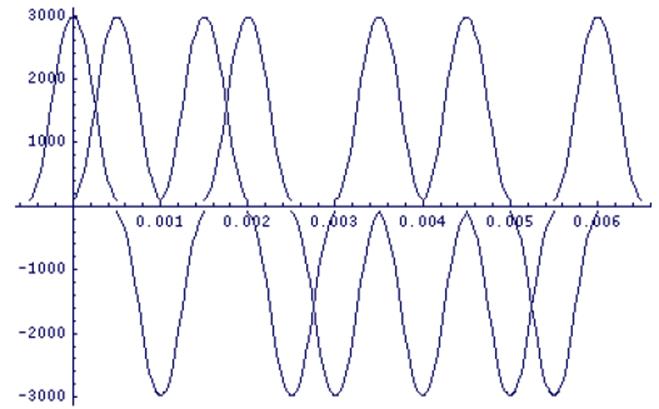
Рис. 3.5. Преобразование фильтром входной последовательности

Суммарный сигнал на выходе фильтра b(t) имеет вид:

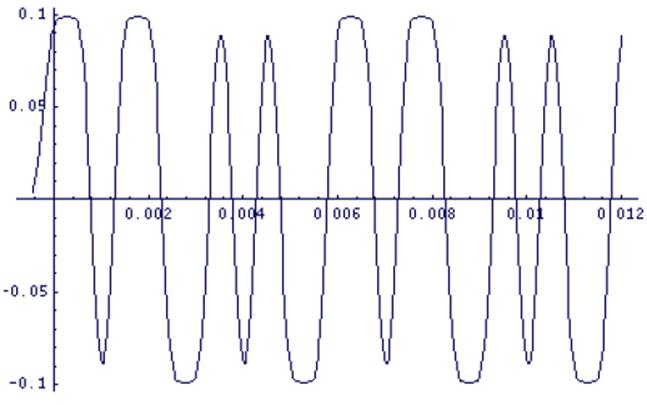
Рис. 3.6. Сигнал b(t) на выходе гауссовского фильтра

С выхода фильтра сигнал b(t) поступает на интегратор, формируется интегрированный сигнал c(t):

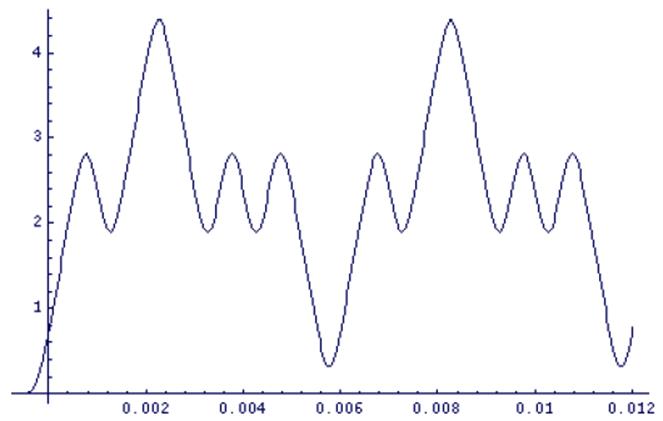
Рис. 3.7. Интегрированный сигнал c(t)

Сигнал c(t) преобразуется в сигналы I(t) и Q(t) по законам:

                                               (3.9)

                                             (3.10)

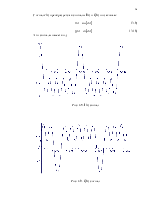
Эти сигналы имеет вид:

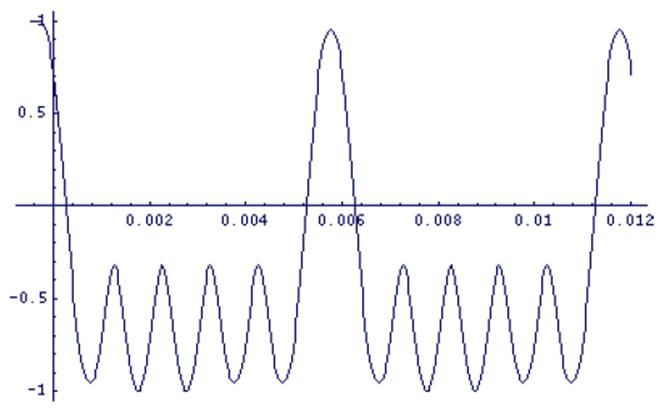
Рис. 3.8. I(t) сигнал

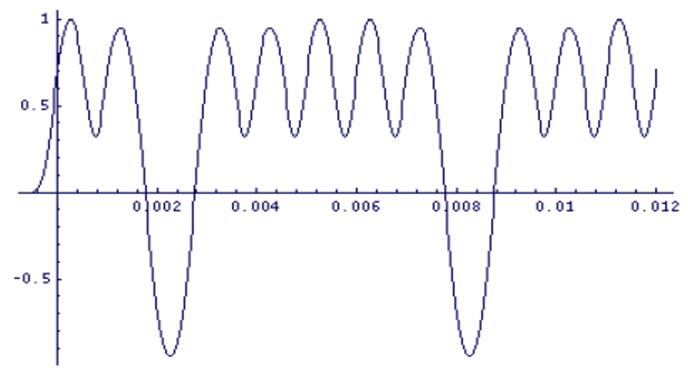
Рис. 3.9. Q(t) сигнал

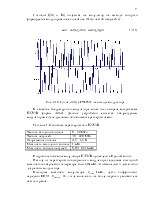
Сигналы Q(t) и I(t) подаются на модулятор на выходе которого формируется модулированное колебание m(t) с частой несущей f_с :

                              (3.11)

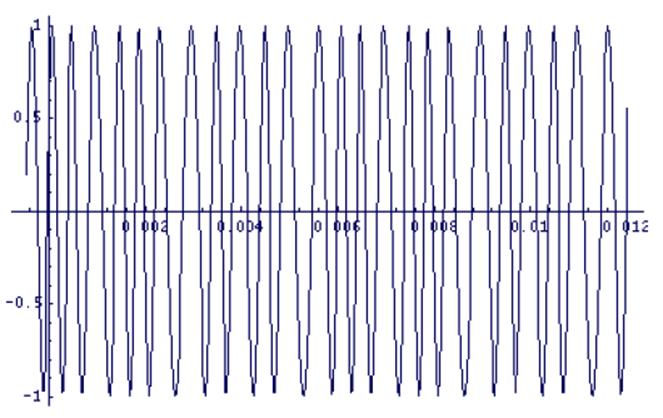
Рис. 3.10. Сигнал m(t) с ГЧММС на выходе модулятора

В качестве квадратурного модулятора мною был выбрана микросхема U2793B фирмы Atmel. Данное устройство является квадратурным модулятором со следующими основными характеристиками:

Таблица 1. Основные характеристики U2793B

Подробное описание модулятора U2793B приведено в Приложении 4.

Исходя из характеристик выбранного модулятора зададимся выходной мощностью кварцевого генератора мВт. Этой мощности достаточно для работы модулятора.

Выходная мощность модулятора мВт, пусть коэффициент передачи КПУ1 , тогда мощность на входе первого умножителя частоты равна:

;                                    (3.12)

 Вт;

Тогда мощность на входе КПУ2 равна:

;                                     (3.13)

Вт;

Следовательно КПУ2 должен иметь коэффициент передачи:

;                                 (3.14)

;

Произведём частотный расчёт передатчика. Частота на выходе передатчика МГц. Частота на входе УЧ3:

 МГц;                       (3.15)

Частота на входе УЧ2:

МГц;                       (3.16)

Частота на входе УЧ1 равна частоте генерируемой кварцевым