Разработка передатчика американского стандарта беспроводных телефонов PWT, страница 3

Соотношение между абсолютными величинами фазы модулированного колебания из множества {± π/4, ±3π/4}, {0, π/2, π, 3π/2) или любого другого множества и множеством символов (дибитов) цифрового сообщения {00, 01, 10, 11} устанавливается в каждом конкретном случае стандартом на радиоканал и фиксируется в диаграмме фазовых состояний.

Дифференциальная квадратурная фазовая модуляция с минимальным расстоянием между состояниями фазы несущей π/4 (Differential Quadrature Phase Shift Keying - π/4 DQPSK) является специальной формой многоуровневой дифференциальной фазовой модуляции. Сигнал этого вида модуляции может быть демодулирован некогерентным демодулятором аналогично сигналам DBPSK-модуляции. Отличие дифференциального кодирования при модуляции π/4 DQPSK от дифференциального кодирования при модуляции DBPSK состоит в том, что передается относительное изменение не модулирующего цифрового сигнала, а модулируемого параметра, в данном случае фазы монохроматического высокочастотного колебания.

Функциональная схема модулятора для π/4 DQPSK-сигнала практически совпадает с QPSK-модулятором рис. 3.17; алгоритм формирования модулированного сигнала π/4 DQPSK поясняется таблицей 1 и временными диаграммами, представленными на рисунках   . Линейный кодер формирует модулирующий сигнал w(t) с импульсами прямоугольной формы аналогично формированию модулирующего сигнала в QPSK-модуляторе; символьная скорость модулирующего сигнала D = 1/T_s в 2 раза меньше битовой скорости передачи информации R в цифровом сигнале. Формирователь квадратурных компонент вычисляет значения квадратурных компонент х_к, у_к комплексной огибающей на каждом символьном интервале по правилу, указанному в таблице 1.

Таблица 1 –  Алгоритм формирования сигнала π /4 DQPSK

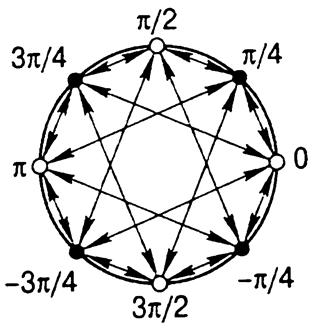
Каждому значению модулирующего сигнала w_k на текущем символьном интервале T_t соответствует не абсолютная величина фазы Θ_k модулированного сигнала, а ее приращение ΔΘ_k, кратное π/4. В результате диаграмма фазовых состояний π/4 DQPSK-сигнала, отражающая допустимые состояния фазы несущей частоты и переходы между ними (рисунок 2 а), является наложением  двух  частных  диаграмм   QPSK-сигнала, повернутых относительно друг друга на угол π/4.

Переход из одного состояния в другое соответствует изменению текущего значения фазы на ±π/4 или ±3π/4, т. е, обязательно от одной частной диаграммы к другой. Главные значения фазы Θ_k, расположены равномерно на тригонометрическом круге с шагом π/4; абсолютная величина фазы Θ_k, равная сумме всех предыдущих фазовых состояний, изменяется с тем же самым шагом. Неограниченность абсолютной величины фазы несущей частоты является характерной чертой модуляции π/4 DQPSK. Для модуляции QPSK абсолютная величина фазы несущей частоты равна одному из четырех возможных значений, которые зависят от передаваемого дибита и располагаются на расстоянии π/2 друг от друга.

Каждая квадратурная компонента x(Θ_k) и y(Θ_k) комплексной огибающей сигнала π/4 DQPSK является пятиуровневым полярным сигналом, множество возможных значений которого {0, ±1/, ±l} отражает 8 возможных различных значений фазы.

Фрагмент модулирующего сигнала, с точностью до размерного множителя совпадающего с абсолютным значением фазы модулированного сигнала, показан на рисунке 3. На этом же рисунке показаны исходная и сглаженная (после формирующего фильтра) квадратурные компоненты комплексной огибающей.

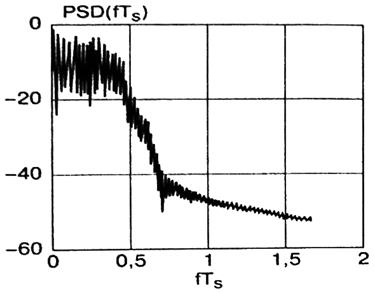
Расчетная спектральная плотность мощности π/4 DQPSK сигнала при использовании фильтра Найквиста «приподнятый косинус» с параметром а=0,35 показана на рисунке 2 б.

а)                                                                  б)

Рисунок 2

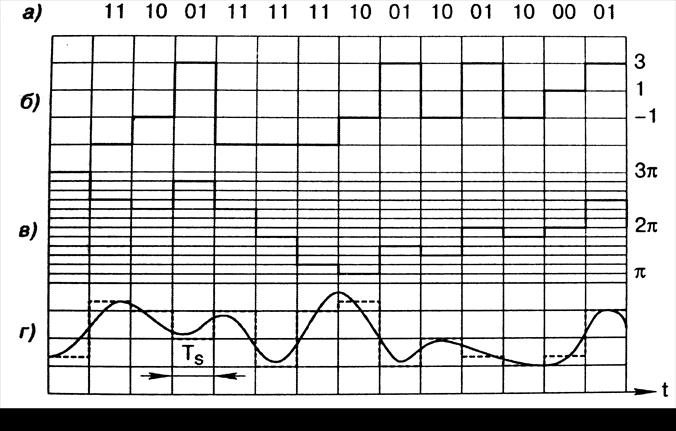
Рисунок 3