Алгоритм Питерсона. Генераторный полином. Кодирование и моделирование канала

BCH коды

> restart:

Алгоритм Питерсона

Алгебра вычислений

with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

Расширенные поля

Если F(q) поля по основанию q и p(x) полином степени m с коэффициентами из поля F(q), но неприводимый в этом поле, то можно получить поле из q^m символов используя аддитивный корень p.

Рассмотрим слкчай, когда p=2.

> p:=2;

определим  alpha - корень полинома p(z) = Z^6+Z+1, m=6.

> alias(alpha=RootOf(Z^6+Z+1) mod p):

> m:=6;

> Q:=p^m;

> powers:=vector(Q-1);

Формирование элементов поля через степени alpha^(i-1)

> for i to Q-1 do powers[i]:=evala(alpha^(i-1)) mod p od:

> print(powers);

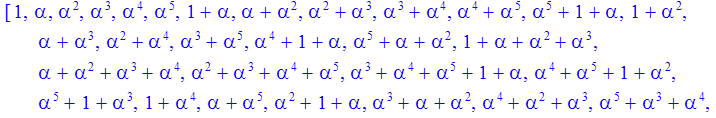
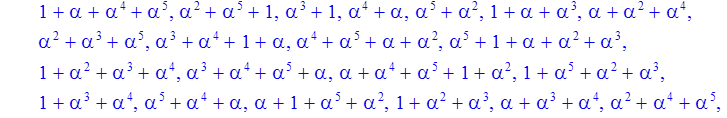
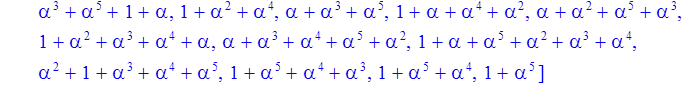
> inverse:=vector(Q-1);

Формирование обратных элементов поля 1/powers[i]

> for i to Q-1 do inverse[i]:=evala(1/powers[i])mod p od:

> print(inverse);

Генераторный полином

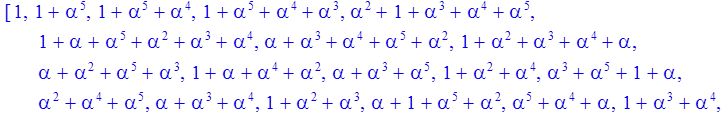
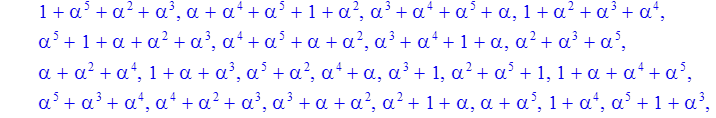
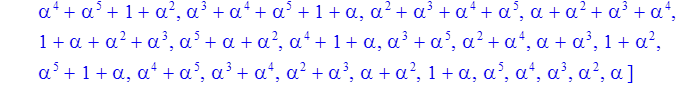
Найдем генераторный полином БЧХ кода. Предварительно определим минимальный полином заданного поля. Предположим, что циклический код формируется по модулю x^63+1, т.е. кодовое слово имеет длину 63. Код поддерживает расширенное поле GF(2^m)

Проведем факторизацию полинома  x^63+1

Вычисление минимальных полиномов через циклотомические классы

Чтение оператора, вычисляющего циклотомический класс s, для  n  и p

>  read "CyclotomicCoset.m";

Пример s=1,n=63,p=2

> CyclotomicCoset(1,63,2);

>

> read "AllCyclotomicCosets.m";  

Чтение оператора, вычисляющего все циклотомические классы

> AllCyclotomicCosets(63,2);

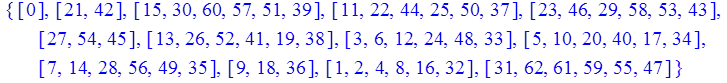
Формирование минимальных многочленов через степени alpha^i, i - числа циклотомического класса

> mn1:=simplify((x+alpha)*(x+alpha^2)*(x+alpha^4)*(x+alpha^8)*(x+alpha^16)*(x+alpha^32)) mod 2;

> mn3:=simplify((x+alpha^3)*(x+alpha^6)*(x+alpha^12)*(x+alpha^24)*(x+alpha^48)*(x+alpha^33)) mod 2;

> mn5:=simplify((x+alpha^5)*(x+alpha^10)*(x+alpha^20)*(x+alpha^40)*(x+alpha^17)*(x+alpha^34)) mod 2;

> mn7:=simplify((x+alpha^7)*(x+alpha^14)*(x+alpha^28)*(x+alpha^56)*(x+alpha^49)*(x+alpha^35)) mod 2;

> mn9:=simplify((x+alpha^9)*(x+alpha^18)*(x+alpha^36)) mod 2;

Формирование минимальных многочленов через факторизацию полинома (x^n-1)

.

> Factor(x^63+1) mod 2;

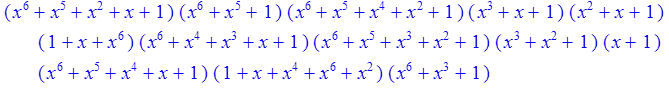
Выделим первый полином

> m1:=x^6+x+1;

> m3:=x^6+x^4+x^2+x+1;

> m5 := 1+x+x^6+x^2+x^5;

Сформируем полином, исправляющий 3 ошибки

> g3:=expand(mn1*mn7*mn9*mn3*mn5) mod 2;

> g3:=sort(g3,x);

Кодирование и моделирование канала

Кодирование

Сформируем информационный вектор

> a:= 1+x+ x^7;

Несистематический код c(x)=a(x)g(x)

> с:=sort(expand(simplify(g5*a))) mod 2;

Систематический код

1. words:=a(x)x^(n-k)

> words:=sort(expand(x^18*a));

Вычисление остатка ww:= rem{a(x)x^(n-k)/g(x))

> ww:=Rem(words,g3,x) mod 2;

Формирование кодового слова

> c:=words+ww mod 2;

Модель канала - через полином ошибок err(x)

> err:= x^4+x^8+x^12+x^16+x^20;

Аддитивная смесь кода и ошибок

> rws:=sort(c+err mod 2);

Принимаемый сигнал

> y:=sort(c+err mod 2);

Вычисление вектора синдромов

Значения синдрома вычисляются путем подстановки в полином y(x) значения соответствующего элемента поля

> s1:=Eval(y,x=alpha) mod 2;

> s2:=Eval(y,x=alpha^2) mod 2;

> s3:=Eval(y,x=alpha^3) mod 2;

> s4:=Eval(y,x=alpha^4) mod 2;

> s5:=Eval(y,x=alpha^5) mod 2;

> s6:=Eval(y,x=alpha^6) mod 2;

Составление матрицы  сдвигов синдромов

> A:=matrix(3,3,[s1,s1^2,s3,s1^2,s3,s1^4,s3,s1^4,s5]);

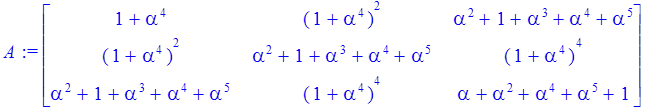
Задание вектора значений синдрома для правой части системы уравнений

> hs:=vector(3,[s1^4,s5,s3^2]);

Решение системы линейных уравнений

> co:=Linsolve(A,hs) mod 2;

Задание полинома локаторов ошибок sig

> sig:=z^3+co[3]*z^2+co[2]*z+co[1];

Факторизация полинома sig для нахождения его корней

> Factor(sig) mod 2;

Нахождение корней полинома локаторов ошибок

> erp:=vector(3);

> ro:=Roots(sig) mod 2;

Пересчет значений корней полинома локаторов ошибок в локаторы ошибок или позиции ошибок

> for i from 1 to 3 do

for j from 1 to 63 do

if (ro[i,1]=powers[j]) then erp[i]:=j-1 fi;

od;od;

Вывод  значений позиций ошибок

> print(erp);

>

>

>

>

>