построим график сплайна и исходной функции на одних осях, а на других — график погрешности:
>> subplot(2, 1, 1)
>> х = -1:0.05:1;
>> у = fun(x);
>> plot( х, у,‘гр’)
>> hold on
>> fnplt(s)
>> title('Графики функции и сплайна')
>> legend('функция', 'сплайн',0)
>> хе = -1:0.01:1;
>> ye = abs(fnval(s, хе) - fun(xe));
>> subplot (2, 1, 2)
>> plot(xe, ye)
>> title('График ошибки')
Получающийся результат приведен на рис. 18.1.
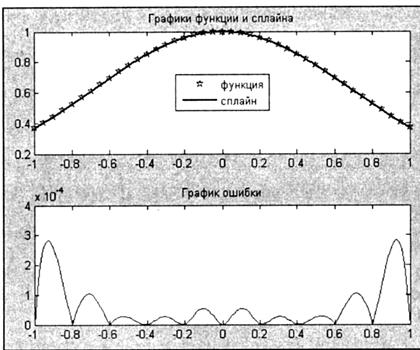
Рис.
18.1 Представление кубического сплайна и погрешность интерполяции для функции у(х)= ![]()
Интерфейс функции csapi позволяет вместо конструирования сплайна в виде структуры вычислить его значения в заданных точках. Создадим вектор с абсциссами точек
» xl = -0.9:0.2:0.9;
и укажем его при обращении к csapi в качестве третьего входного аргумента:
>> value = csapi(x, у, xl);
В вектор value занесены значения кубического сплайна в заданных точках. Обращение csapi(х, у, xl) дает тот же результат, что и fnval(csapi(х, у), xl).
Построение сплайна для вектор - функции
Spline Toolbox позволяет конструировать сплайны для вектор - функций. Для построения, например, кубического сплайна используется рассмотренная выше функция csapi. В случае вектор - функций она вызывается от второго входного аргумента — матрицы, строки которой содержат значения функции в узлах.
Продемонстрируем приближение табличных одномерных данных, каждому значению аргумента которых соответствует два значения функции. Эти значения являются координатами точек, лежащих на кривой, которая называется "улиткой Паскаля" и задается параметрическими зависимостями:
х = a* cos2 t + b* cos t, y = a- cos t * sin t + b* sin t,
где 0 < t < 2π , a > 0, b > 0.
Листинг 18.1 содержит текст файл - функции uiitka2, которая строит улитку Паскаля при помощи кубических сплайнов.
Листинг 18.1. Файл-функция для построения улитки Паскаля
function ulitka2(a, b)
% Построение улитки Паскаля кубическими сплайнами
% Задание шага изменения параметра
h = pi/20;
% Задание значений параметра
t = 0:h:2*pi;
% Вычисление таблицы значений х = a*cos(t).*cos(t) + b*cos(t); у = a*cos(t).*sin(t) + b*sin(t)
% Формирование матрицы со значениями табличной функции
R = [х ; у] ;
% Создание сплайна рр = csapi(t ,R);
о Вывод графика сплайна на оси с одинаковым масштабом
figure
fnplt(pp)
axis equal
Вызов файл-функции
>> ulitka2(2, 1)
приводит к появлению улитки Паскаля (рис. 18.2).
Входными аргументами файл - функции uiitka2 являются геометрические параметры улитки Паскаля а и b. Меняя эти величины, можно получит различные формы улитки. Исходными данными для построения сплайна являются равноотстоящие точки с шагом h, помещенные в t, и соответствующие им координаты х, у точек на кривой — координаты радиус вектора улитки r . Функция csapi строит кусочно-полиномиальную форму кубического сплайна, который затем отображается графически при помощи fnplt.
|
|
Рис. 18.2. Улитка Паскаля, построенная с помощью применения кубического сплайна, при значениях параметров a = 2, b = 1
Примечание
Для некоторых функций, в том числе и для рассмотренной csapi происходит усреднение значения функции, если приближаемая функция много-; значна, т. е. таблица содержит несколько одинаковых значений аргумента
Произвольные краевые условия
Как уже отмечалось выше, функция csapi строит сплайн с условиями "отсутствия узла". Эти условия дают наиболее точное представление интерполируемой функции, если нет информации об ее производных на границах рассматриваемого отрезка. При наличии каких-либо дополнительных данных о приближаемой функции, зачастую, целесообразно поставить другие краевые условия. Для этого применяется функция csape. Она допускает различные варианты обращения. Первый способ
s = csape(х, у)
приводит к построению кусочно-полиномиальной формы интерполяционного кубического сплайна с краевыми условиями, заданными по умолчанию (ниже мы скажем, что это за условия). Вызов csape с третьим входным гументом
s = csape(х, у, conds)
позволяет выбрать краевые условия из довольно обширного списка, представленного в табл. 18.1. При этом может потребоваться расширение массива у для указания значений производной сплайна на границах отрезка. Возможно также задание собственных граничных условий, но тогда параметр conds должен быть не текстовой строкой, а вектор-строкой из двух элементов. При таком способе можно определить различные краевые условия. При этом значение первого элемента соответствует левой границе отрезка, а второго — правой. В массив у при этом добавляются дополнительные значения в начало и конец массива. Приняты следующие правила: если значение элемента вектора строки conds равно 1, то дополнительный элемент в у задает значение первой производной, если в conds элемент равен 2, то дополнительный элемент в у задает значение второй производной. В случае периодических условий conds задается массивом [0 0] и обращения si = csape
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.