Другие предметы \ Технические средства автоматизации и управления

Разработка технического предложения о возможности реализации системы электропривода по требованиям технического задания, страница 2

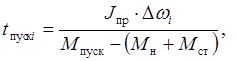
Согласно выражению (3), расчетная формула времени пуска имеет вид

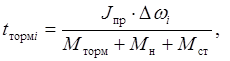
где М_торм – тормозной момент двигателя.

Таблица 4

Время пуска и торможения для каждого момента времени

Номер интервала	1	2	3	4	5	6	7
t_пуск, мс	72,16	96,22	96,22	144,33	144,33	192,43	192,43
t_торм, мс	53,16	70,88	70,88	106,32	106,32	141,76	141,76

Ток при пуске, торможении и установившемся движении, для построения диаграмм зависимости токов от времени, А:

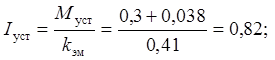
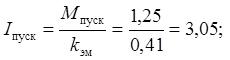
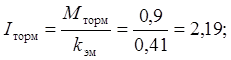
где - момент при установившемся режиме.

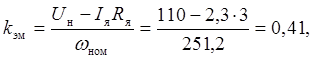, где 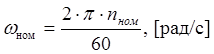- номинальная частота вращения вала двигателя.

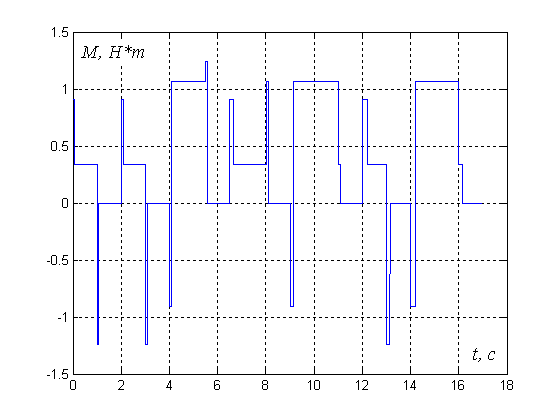
Рис.2 Диаграмма пусковых и тормозных моментов на двигателе

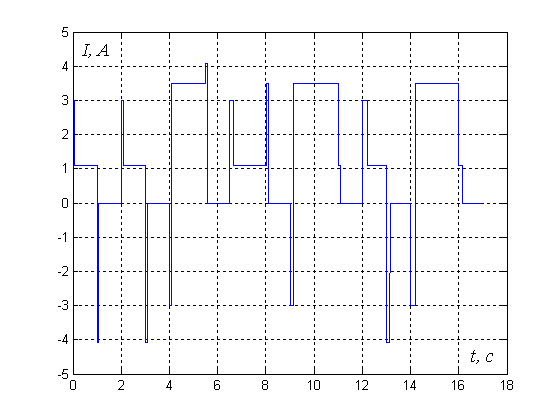
Рис.3 Диаграмма пусковых и тормозных токов на двигателе

3.4 Оценка тепловой нагрузки двигателя

Проведем оценку тепловой нагрузки двигателя, используя метод эквивалентного момента

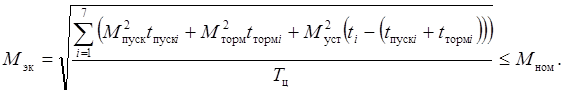
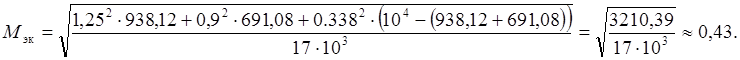
Проведем оценку тепловой нагрузки двигателя, используя метод эквивалентного тока

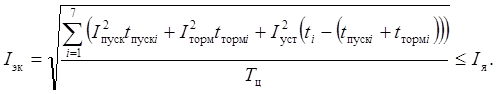
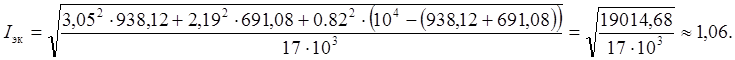
Условия по эквивалентному моменту и току удовлетворяют выбору двигателя постоянного тока «СЛ-621».

3.5 Оценка параметров динамической модели двигателя и усилителя мощности.

Разработка функциональной модели ДПТ НВ для моделирования [2] в среде MatLab 6.5 выполняется под вид уравнений, приведенных ниже:

где относительные переменные состояния двигателя:

;

параметры двигателя

Расчеты ведутся в относительных единицах, но при выводе результатов моделирования относительные единицы приводятся к номинальным значениям выбранного двигателя. Функциональные модели ДПТ и нагрузочного момента приведены на рис.4, рис.5.

Электромагнитная постоянная времени, с:

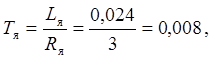
где L_я– индуктивность обмотки якоря, Гн:

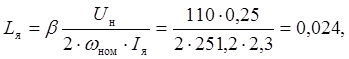
где β = 0,25 – эмпирический коэффициент.

Постоянная времени обмотки возбуждения, с:

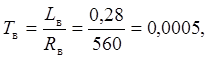
где L_в – индуктивность обмотки возбуждения, Гн:

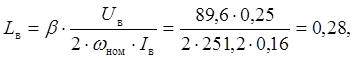
где U_в– напряжение обмотки возбуждения.

Электромеханическая постоянная времени, с:

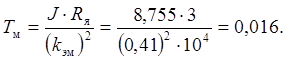
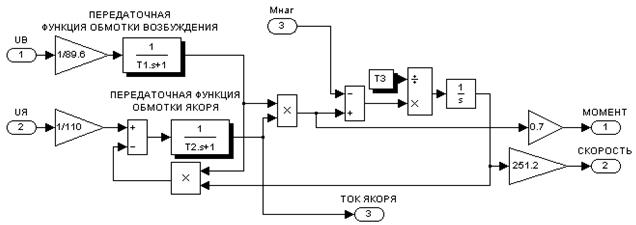
Рис.5 Блок – диаграмма ДПТ НВ

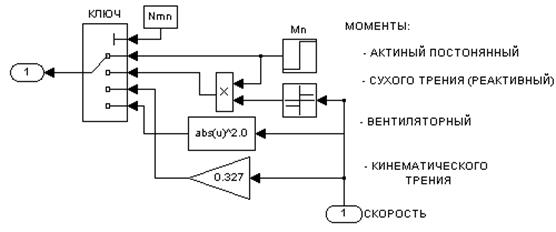
Рис.6 Блок – диаграмма реализации нагрузочного момента

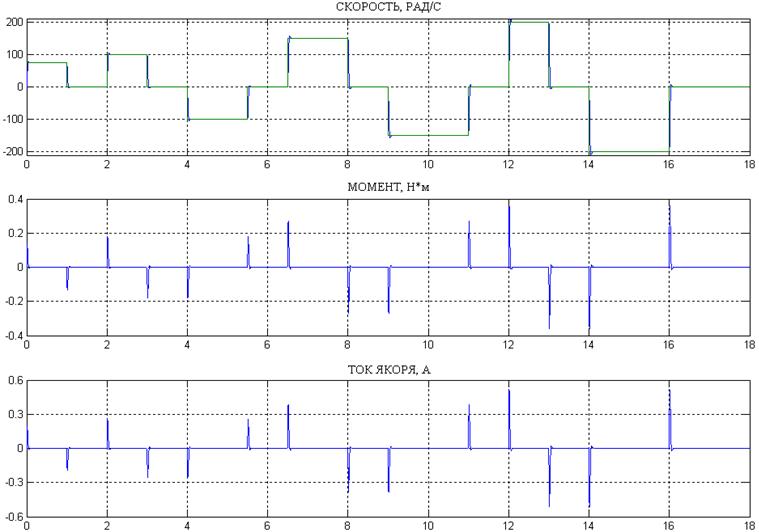
Рис.7 Результаты моделирования разомкнутой системы без нагрузочного момента

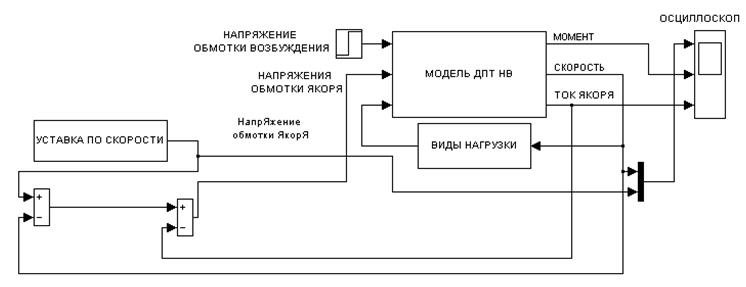
Рис.8 Модель привода на основе ДПТ НВ

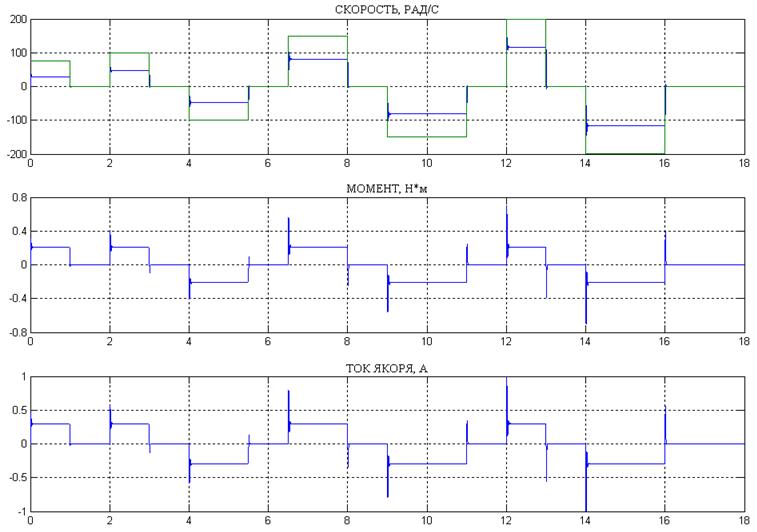
Рис.9 Результаты моделирования замкнутой системы с нагрузочным моментом

Результаты моделирования замкнутой системы с приложенным моментом нагрузки свидетельствуют о необходимости системы регулирования ДПТ НВ. Система регулирования для данного двигателя будет рассчитана методом синтеза регуляторов в подчиненных системах электропривода, источник метода [2].

Синтез регуляторов для внутреннего и внешнего контуров схемы будет реализованы так, чтобы при включении регулятора последовательно с соответствующим звеном системы была скомпенсирована большая постоянная времени и взамен ее действовала существенно меньшая постоянная времени .

Звено внутреннего контура схемы является апериодическим с передаточной функцией 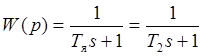и регулятор должен иметь передаточную функцию, соответствующую ПИ–регулятору,

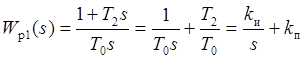. Постоянную времени интегратора примем равной электромагнитной постоянно времени, т.к. очень мало. Тогда коэффициенты ПИ – регулятора примут следующие значения:

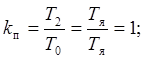
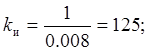
Звено внешнего контура схемы является интегратором с передаточной функцией 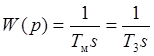и регулятор должен иметь передаточную функция, соответствующую П – регулятору, . Причем 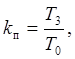где может иметь любое малое значение. Примем , тогда передаточная функция П – регулятора будет иметь вид

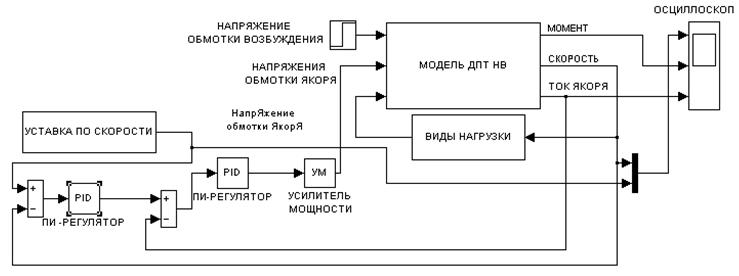
Рис.10 Модель привода на основе ДПТ НВ с системой регулирования

Моделирование замкнутой системы с синтезированными выше регуляторами не обеспечило нулевой ошибки в статике. Фрагмент результатов моделирования приведен на рис.11. Поэтому необходимо использовать ПИ – регулятор для внешнего контура. Ввод интегратора с достаточно малым коэффициентом позволит обеспечить требование нулевой ошибки в статике. Примем , тогда передаточная функция регулятора по скорости будет иметь вид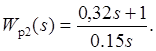

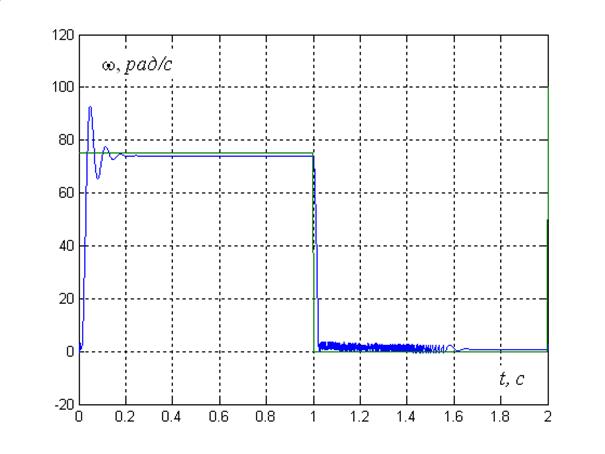
Рис.11 Фрагмент результатов моделирования с П – регулятором по скорости

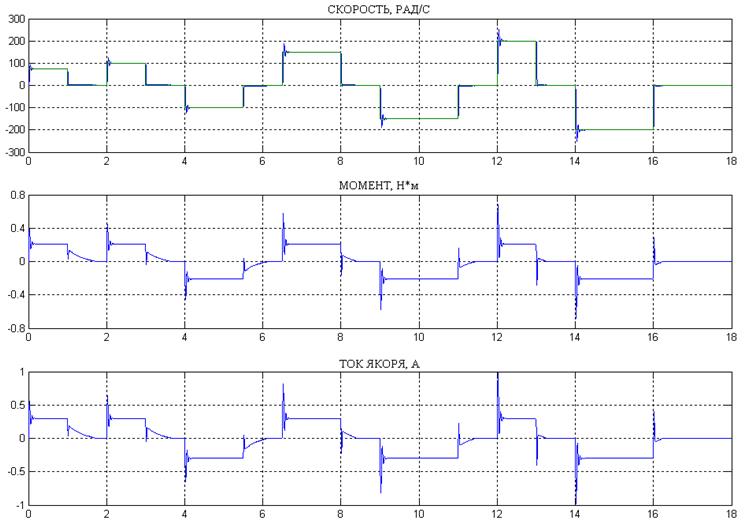
Рис.12 Результаты моделирования замкнутой системы с ПИ – регуляторами.

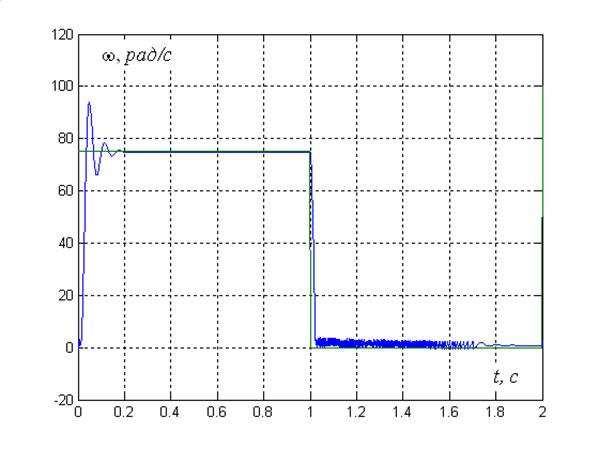
Рис. 13Фрагмент результатов моделирования с ПИ – регулятором по скорости

В результате моделирования удалось обеспечить нулевую ошибку в статике. Ток якоря и момент не превышают номинальных значений. Разгон выполняется за 0,032с, что составляет примерно четыре электромагнитных постоянных времени. Переходный процесс длится 0,11с. Перерегулирование составляет порядка 27%.

4. Заключение

Выбранный двигатель, удовлетворяющий требованиям технического задания – «СЛ - 621». Регулятор, рассчитанный согласно [2] для подчиненных систем, не дал удовлетворительных результатов (в частности по ошибки в статике), поэтому в схему был введет коэффициент интегрирования для внешнего контура обратной связи. Таким образом, система регулирования представляет собой два ПИ – регулятора. Один для внутреннего контура схемы (обратная связь по току), второй – внешнего (обратная связь по скорости). Из результатов моделирования следует, что реализовать систему электропривода по требованиям технического задания возможно.

5. Список литературы

1. Волков Н.И., Миловзоров В.П. Электромашинные устройства автоматики:Учеб. для вузов по спец. «Автоматика и телемеханика». – 2-е изд. – М.: Высшая школа, 1986.

2. Герман-Галкин М.И. Моделирование электротехнических устройств в среде MatLab.

1 2

Скачать файл