Разработка предложения технического о возможности реализации системы стабилизации температуры воды в электрокалорифере по требованиям технического задания, страница 2

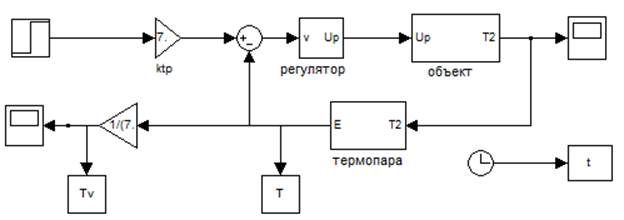
Рис.3. Блок-диаграммма системы.

Модель термопары (рис.4.) состоит из звена второго порядка с передаточной функцией:

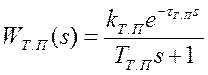
Подбором коэффициентов была обеспечена кривая переходного процесса с заданными параметрами(рис. 5.).

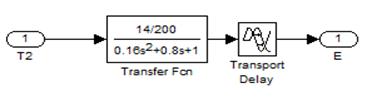
Рис.4. Блок-диаграммма термопары.

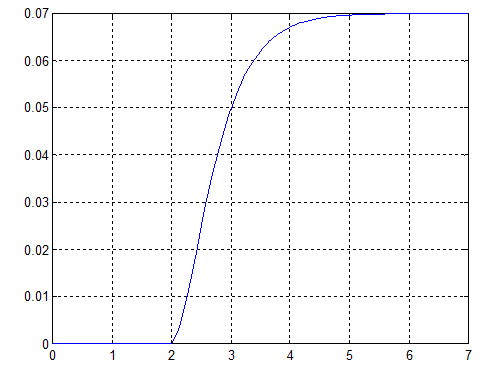
Рис.5. График переходного процесса термопары по управлению.

Блок-диаграмма объекта представлена на рис.6.  Основные блоки -  источник питания( рис. 7.), нагреватель( рис. 8.), калорифер( рис. 9 - 12.).

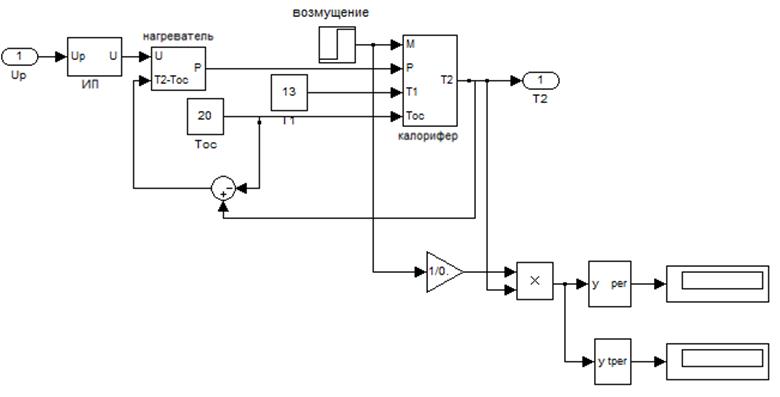
Рис.6. Блок-диаграммма объекта.

В устройстве калорифера имеется теплоэлектронагреватель (ТЭН), величина мощности которого определяется в соответствии с законом Джоуля-Ленца и учетом изменения величины сопротивления в зависимости от температуры по линейному закону.

,

где      – сопротивление ТЭНа в холодном состоянии, Ом;

α = 0,022 – термический коэффициент, 1/^oC.

Модель нагревателя изображена на рис.7.

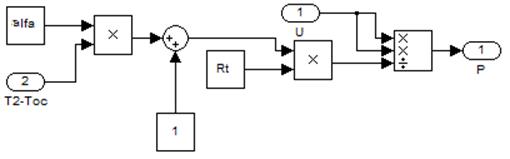
Рис. 7. Блок-диаграммма нагревателя.

Модель источника питания представлена на рис.8. Предполагается, что рабочая точка находится на линейной части характеристики источника питания. 

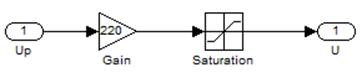
Рис.8. Блок-диаграммма источника питания.

С учетом представлений о тепловом динамическом балансе математическую модель для определения температуры воды в баке калорифера при структурном моделировании её динамических свойств необходимо представить в соответствии с выражением:

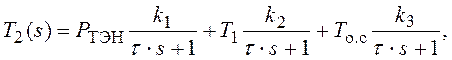
где     ; ; ; .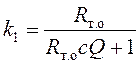

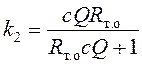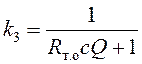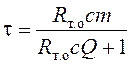Поскольку реализовать передаточную функцию с переменной постоянной времени не удалось, рассчитав её значение при мощности, равной один киловатт, примем τ=100с. Расчет параметров k₁, k₂, k₃ осуществляется в блоках, представленных на рис. 10 - 12_.

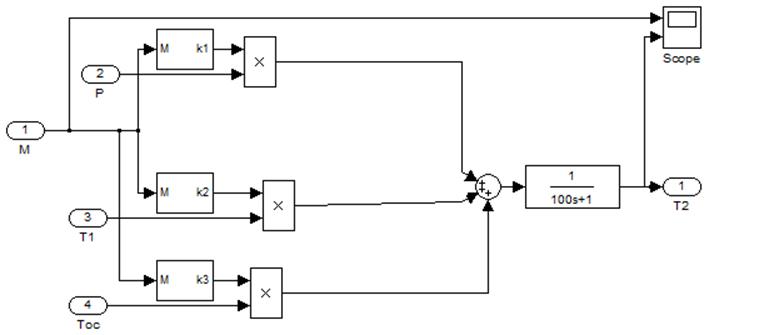
Рис.9. Блок-диаграммма модели калорифера.

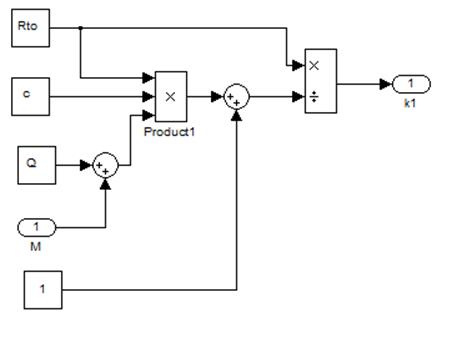
Рис.10. Блок-диаграммма расчета к1

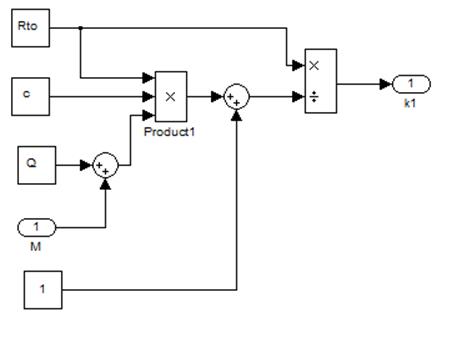
Рис.11. Блок-диаграммма расчета к2

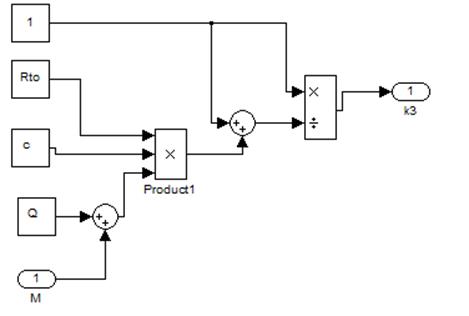
Рис.12. Блок-диаграммма расчета к3.

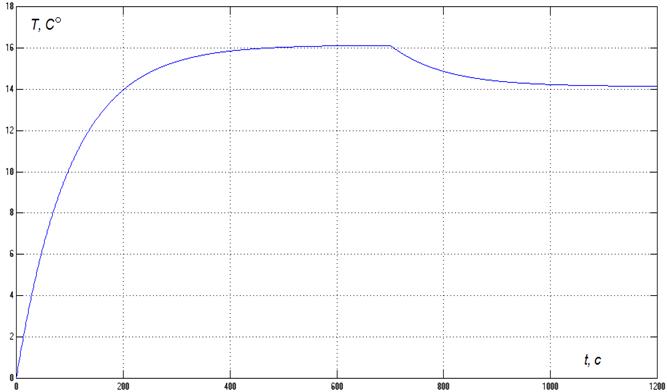
Рис.13. График переходного процесса объекта по управлению и возмущению.

Длительность переходного процесса по возмущению: 80с  Перерегулирование: 0%

Характеристики объекта: Т= 350 с, τ= 1 с.

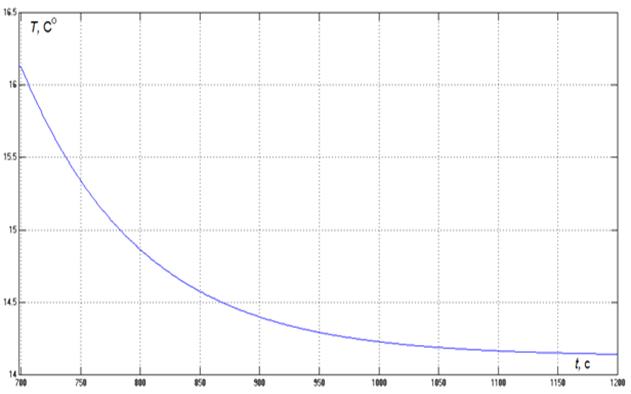
Рис.14. График переходного процесса объекта по возмущению.

3.  СИНТЕЗ РЕГУЛЯТОРА

Поскольку переходный процесс по возмущению не колебательный, для регулирования пропорционально-интегрального закона будет достаточно. Наиболее распространенным на практике является ПИ-регулятор.

ПИ-регулятор обладает следующими достоинствами:

1.  Обеспечивает нулевую статическую ошибку регулирования.

2.  Достаточно прост в настройке, т.к. настраиваются только два параметра (коэффициент усиления и постоянная интегрирования ) В таком регуляторе имеется возможность оптимизации , что обеспечивает управление с минимально возможной средне-квадратичной ошибкой регулирования.

3.  Малая чувствительность к шумам в канале измерения (в отличии от ПИД-регулятора).

Модель регулятора приведена на рис.15.

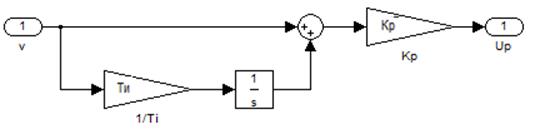
Рис.15. Блок-диаграммма регулятора.

Поскольку отношение постоянных времени объекта мало, метод настройки по номограммам применить невозможно. Синтез регулятора осуществляется формульным методом. Метод используется для быстрой, приближенной оценки значений параметров настройки регулятора. Расчетные формулы[2]:

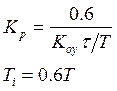
Полученные значения: Kp=9.3         Ti=1320 c

Проведем эксперимент при различных значениях K_p и T_i.(рис. 16)

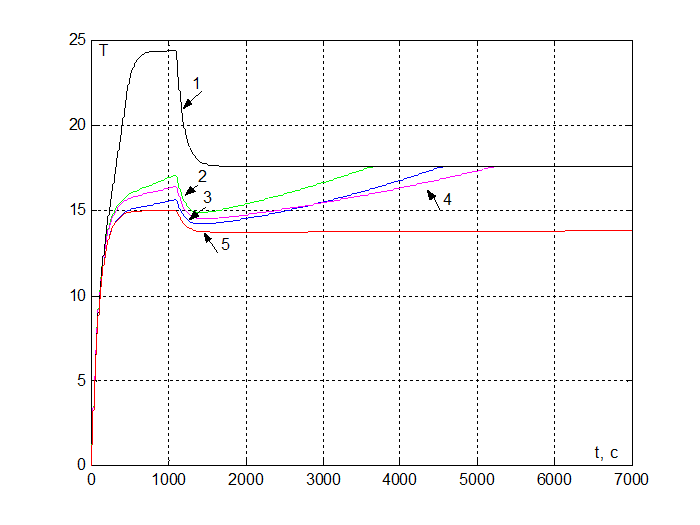
Рис.16. Графики переходного процесса объекта при различных значениях параметров регулятора (1 - K_p= 1, T_i= 10,2 - K_p= 10, T_i= 1000,3 - K_p=1 , T_i=100 ,4 - K_p=9.3 , T_i=1320 , 5 - K_p= 1, T_i=100 ).

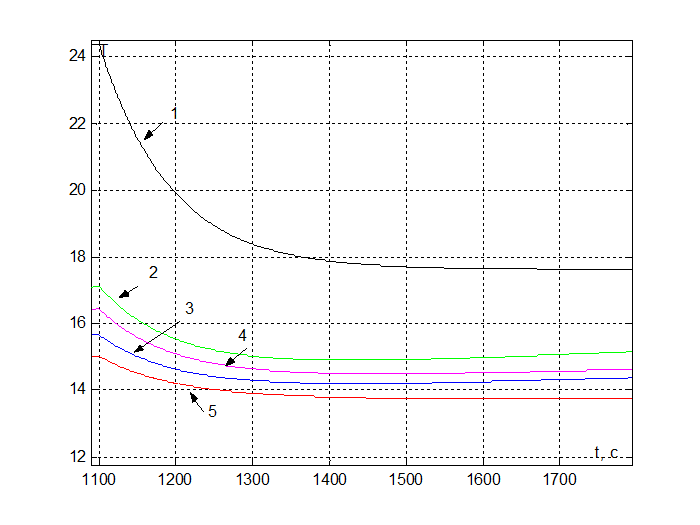
Рис.17. Графики переходного процесса объекта возмущению при различных значениях параметров регулятора (1 - K_p= 1, T_i= 10, 2 - K_p= 10, T_i= 1000, 3 - K_p=1 , T_i=100 , 4 - K_p=9.3 , T_i=1320 , 5 - K_p= 1, T_i=100 ).

В результате эксперимента получили переходные процессы со следующими характеристиками. Длительность переходного процесса:

1- 280 с

2- 248 с

3- 200 с

4- 225 с

5- 250 с

Перерегулирование:

1-  0%

2-  0%

3-  0%

4-  0%

5-  0%

С помощью регулятора удалось уменьшить длительность переходного процесса. График 1 отражает ситуацию, когда в системе переизбыток энергии для отработки возмущения. График 5 отражает обратную ситуацию.  На основании графиков 3,4 можно убедиться в том, что метод действительно приближенный, поскольку лучшими характеристиками обладает  переходный процесс не с расчетными коэффициентами, а с коэффициентами близкими к этим значениям. В результате примем следующие настройки: Kp=10       Ti=1000 c

ЗАКЛЮЧЕНИЕ

В результате разработана модель системы стабилизации воды в электрокалорифере. В качестве закона управления выбран ПИ-регулятор. Настройка коэффициентов регулятора осуществлялась формульным методом.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.  Гультяев А.К. Визуальное моделирование в среде MATLAB: Учебный курс. СПб: Питер, 2000. 432 с.

2.  www.compitech.ru/html.cgi/arhiv/03_05/stat_114.htm

3.  www.vodogreev.ru