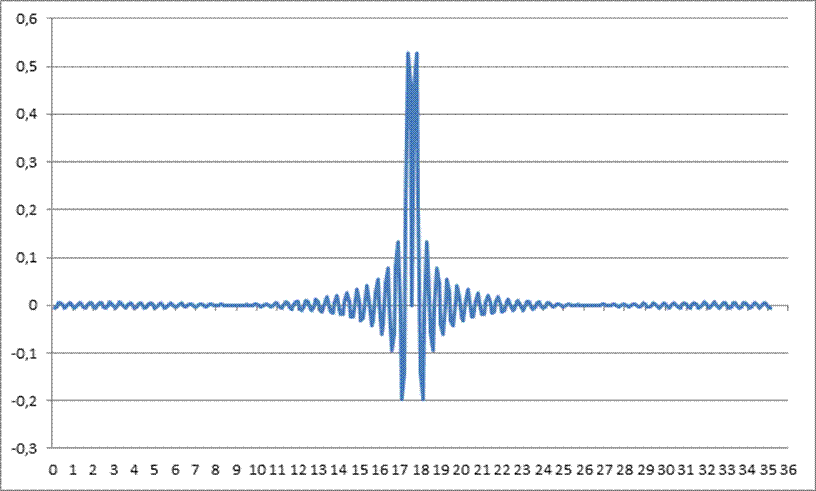
Другие предметы \ Автоматизация проектирования систем и средств управления

Расчет нерекурсивного фильтра на основе модифицированного гармонического ряда Фурье. Приобретение навыков проектирования и расчета нерекурсивных фильтров, страница 6

Рис. 1. Импульсная характеристика

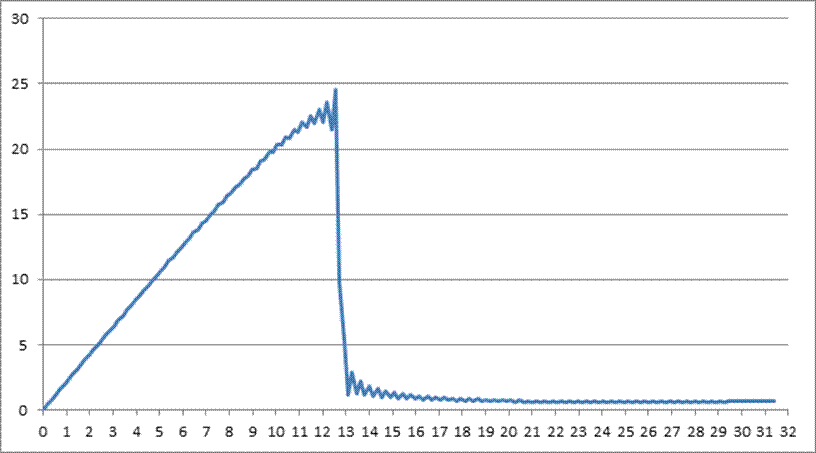
Рис. 2. Амплитудно-частотная характеристика

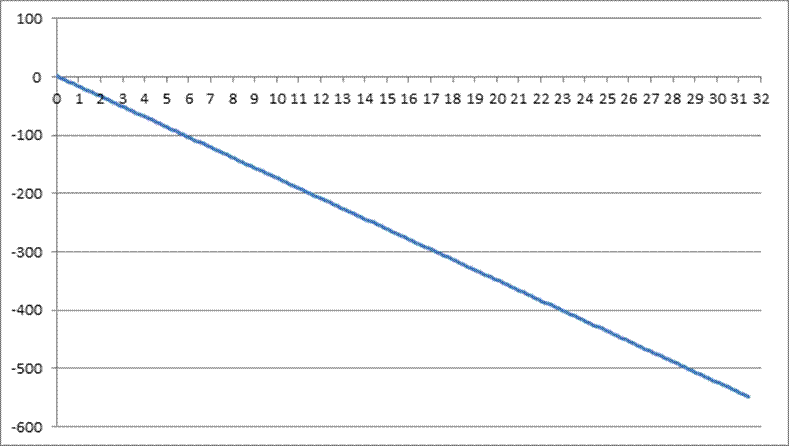
Рис. 3. Фазо-частотная характеристика

Выводы

В ходе расчетно-графической работы спроектирован дифференцирующий фильтр, АЧХ которого отличается от теоретического наличием колебаний на границах переходной полосы, что объясняется особенностями аппроксимации АЧХ фильтра гармоническим рядом Фурье и зависит от выбора сглаживающего множителя при переходе к модифицированным гармоническим рядам.

ФЧХ фильтра линейная, фазовая задержка tф=17с.

График импульсной характеристики симметричен относительно значения времени t=17,6с, которому соответствует L=175.


Приложение

Листинг программы

SubDF_rass4et()

' Исходные данные

Const Om_F = 12      ' верхняя граничная частота полосы пропускания

Const d_om_n = 1.5   ' ширина переходной полосы

Const L = 175        ' количество членов ряда Фурье

Const Kf = 1.5       ' коэффициент усиления фильтра в полосе пропускания

Const dt = 0.1       ' шаг дискретизации по времени

Const Pi = 3.14      ' число Пи

Const ro = 0.54      ' коэффициент Хэмминга

' Объявление переменных

Dim om_B As Single  ' полупериод повторения АЧХ

Dim Om_p As Single  ' верхняя граничная частота полосы пропускания

Dim sigma As Single ' множительХэмминга

Dim sumT As Single  ' время

Dim k As Integer, i As Integer ' индексыдляциклов

Dim a0 As Single, ak As Single ' коэффициентырядаФурье

Dim wk As Single  ' отсчетыИХ

Dim Aw As Single  ' значениеАЧХ

Dim Fw As Single  ' значениеФЧХ

Dim w As Single   ' частота

Dim sum As Single ' аккумулятордляАЧХ

' Вычисление требуемых частот

om_B = Pi / dt           ' полупериод повторения АЧХ

Om_p = Om_F + d_om_n / 2 ' верхняя граничная частота полосы пропускания

'Вычисление отсчетов dt

Cells(1, 5) = "Время"

For k = 1 To (2 * L + 1)

sumT = sumT + dt

Cells(k + 1, 5) = sumT

Next

'Вычисление множителей Хэмминга

Cells(1, 6) = "Множители"

For k = 1 To (L + 1)

sigma = ro * (1 - ro) * Cos(k * Pi / L)

Cells(k + 1, 6) = sigma

Next

'Вычисление коэффициентов ряда Фурье

Cells(1, 7) = "Коэффициенты"

a0 = 0

Cells(2, 7) = a0

For k = 1 To L

ak = 2 * om_B * (Sin(k * dt * Om_p) - k * dt * Om_p * Cos(k * dt * Om_p)) / (k * Pi) ^ 2

Cells(k + 2, 7) = ak

Next

'Вычисление отсчетов ИХ

Cells(1, 10) = "ОтсчетыИХ"

For k = 0 To (2 * L)

If k < L Then

sigma = Cells(L - k + 2, 6)

ak = Cells(L - k + 2, 7)

wk = 0.5 * sigma * ak

Cells(k + 2, 10) = wk

Else

sigma = Cells(k - L + 2, 6)

ak = Cells(k - L + 2, 7)

wk = 0.5 * sigma * ak

Cells(k + 2, 10) = wk

End If

Next

'Вычисление АЧХ и ФЧХ

Cells(1, 11) = "Частота"

Cells(1, 12) = "Отсчеты АЧХ"

Cells(1, 13) = "Отсчеты ФЧХ"

i = 1

For w = 0 To om_B Step (om_B / L)

sum = 0

For k = 1 To L

ak = Cells(L - k + 2, 7)

sum = sum + ak * Sin(k * dt * w)

Next

Cells(i + 1, 11) = w                ' частота

Aw = Abs(2 * sum)

Cells(i + 1, 12) = Aw               ' АЧХ

Fw = Pi / 2 - L * dt * w

Cells(i + 1, 13) = Fw               ' ФЧХ

i = i + 1

Next

End Sub

Скачать файл