Використання ЕОМ при прийнятті управлінських рішень, страница 2

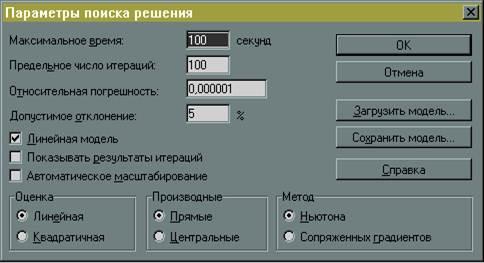
Рис.10

Для вирішення завдання у вікні «Пошук рішення» натиснути кнопку «Виконати». Якщо рішення знайдено з'являється вікно (рис.11):

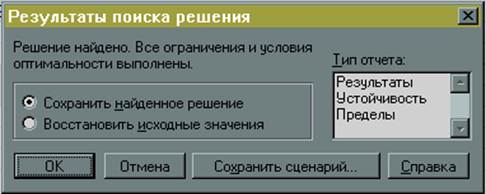
Рис.11

Для перегляду результатів вибираємо тип звіту: «Результати» і натискаємо кнопку ОК. У що з'явилися трьох таблицях (рис.15) наводяться результати пошуку. З цих таблиць видно, що в оптимальному рішенні:

виробництво фарби 1 = B3 = 0.6;

виробництво фарби 2 = С3 = 1.2;

при цьому дохід = D4 = 2.4;

витрата ресурсу A = D7 = 3;

витрата ресурсу B = D8 = 3;

таким чином, обидва ресурсу дефіцитні (відповідні обмеження називаються пов'язаними).

Целевая ячейка (Макс)
	Ячейка	Имя	Исходно		Результат
	$D$4	Доход	2,4		2,4
Изменяемые ячейки
	Ячейка	Имя	Исходно		Результат
	$B$3	Краска 1	0,6		0,6
	$C$3	Краска 2	1,2		1,2
Ограничения
	Ячейка	Имя	Значение	Формула			Состояние		Разница
	$D$7	A Расход	3	$D$7<=$E$7			связанное		0
	$D$8	B Расход	3	$D$8<=$E$8			связанное		0
	$B$3	Краска 1	0,6	$B$3>=0			не связан.		0,6
	$C$3	Краска 2	1,2	$C$3>=0			не связан.		1,2

Рис.12

    «Звіт за результатами» складається з трьох таблиць (рис.12):

в таблиці 1 наводяться відомості про цільової функції;

у таблиці 2 наводяться значення змінних задачі;

у таблиці 3 показані результати пошуку для обмежень задачі.

Первісна таблиця EXCEL заповнюється результатами, отриманими при вирішенні (на Рис.13 що з'явилися значення в темних комірках).

 

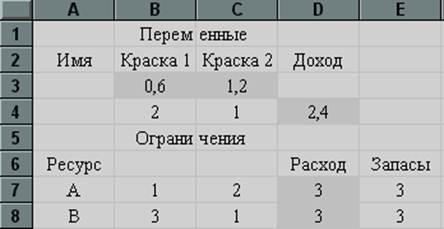
Рис.13

Задача 2. Фірма, що обслуговує туристів, які прибувають на відпочинок, повинна розмістити їх в 4 готелях: “Морський”, “Сонячний”, “Слава” і “Затишний”, в яких заброньовано відповідно 5, 15, 15 і 10 місць. П'ятнадцять туристів прибувають по залізниці, двадцять п'ять прилітають черговим рейсом в аеропорт, а п'ять чоловік прибудуть на теплоході на морський вокзал. Транспортні витрати при перевезенні з пунктів прибуття в готелі приведені в таблиці 1.

Таблиця 1 – Вихідні дані

Вихідний пункт, i		Пункт призначення (готелі), j
		Морський	Сонячний	Слава	Затишний
		1	2	3	4
Залізничний вокзал	1	10	0	20	11
Аеропорт	2	12	7	9	20
Морський вокзал	3	0	14	16	18

В умовах жорсткої конкуренції фірма повинна мінімізувати свої витрати, значну частину яких складає саме транспортні витрати. Потрібно визначити такий план перевезення туристів з пункту прибуття в готелі, при якому сумарні транспортні витрати будуть мінімальні і всі туристи будуть розміщені в готелях.

Розв’язання

1) Введення даних. Вводимо дані таблиці 1 і 2 в осередку EXCEL (рис.14).

В осередках B3: E5 введені вартості перевезень (табл. 2).

В осередках F3: F5 знаходиться число прибувають туристів. А в осередках B6: E6 знаходиться число місць в готелях. Осередки B8: E10 - робочі (змінюються) осередки, у яких будуть обчислюватися значення змінних задачі Xij.

В осередках F8: F10 потрібно записати формули для обчислення лівих частин обмежень (3)¸(5):

в F8 повинна бути сума осередків B8: E8;

в F9 повинна бути сума осередків B9: E9;

в F10 повинна бути сума осередків B10: E10.

Формули для обчислення лівих частин обмежень (6)¸(9) введемо в комірки B11: E11:

в B11 повинна бути сума осередків B8: B10;

в C11 повинна бути сума осередків C8: C10;

в D11 повинна бути сума осередків D8: D10;

в E11 повинна бути сума осередків E8: E10;

Цільову функцію помістимо у комірку G3:

G3: СУММПРОІЗВ (B3: E5; B8: E10).

Таблиця вихідних даних має вигляд (Рис.14):

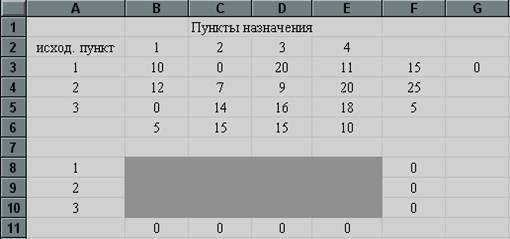
Рис.14

2) Заповнення вікна процедури «Пошук рішення».

цільова функція: G3;

значення цільової функції: min;

змінювані осередку: B8: E10;

обмеження завдання:

F8: F10 = F3: F5 (формули (3)  (5))

B11: E11 = B6: E6 (формули (6)  (9))

B8: E10 0 (1) і B8: E10 - цілі числа (2)

У вікні «Параметри» встановити «Лінійна модель», що відповідає рішенню задачі симплекс-методом. Результати заповнення вікна показані на рис.15:

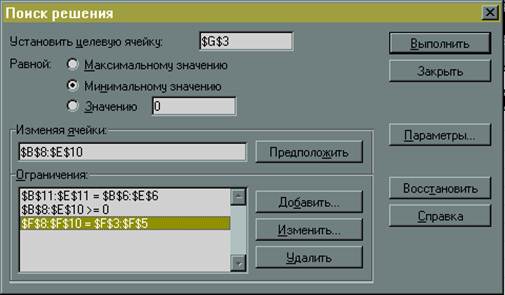
Рис.15

3) Виконавши процедуру «Пошук рішення» отримаємо наступні результати (рис.16):

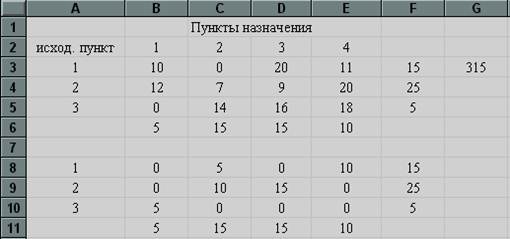
Рис.16

Таким чином із залізничного вокзалу (вихідний пункт 1) слід 10 туристів відвезти в готель «Затишний» (пункт 4) і 5 туристів у готель «Сонячний» (пункт призначення 2); з аеропорту (вихідний пункт 2) 10 туристів відвезти в готель « Сонячний »(пункт призначення 2) і 15 туристів у готель« Слава »(пункт призначення 3); туристів прибувають на морський вокзал (вихідний пункт 3) потрібно відправити в готель« Морський »(пункт призначення 1). Всі ці результати помітні в кінцевій таблиці (рис.19) При цьому сумарна вартість транспортних витрат складе 315 рублів (осередок G3).

14.3 Використання прикладного рішення для завдань торії ігор

Задача 3. Нехай біматрічная гра описується платіжними матрицями

       

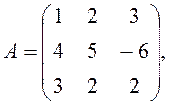
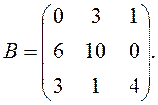
Припускаючи, що гравець А має можливість обрати лише свою чисту стратегію, знайти його оптимальну стратегію.

Розв’язання

Для гравця У отримуємо наступну задачу лінійного програмування:

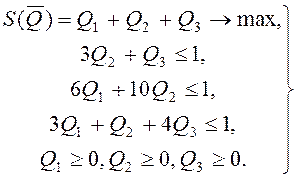
Заповнимо робочий лист, як на рис. 1. Осередок A3, B3, C3 привласнимо імена Q_1, Q _2, Q_3 відповідно.

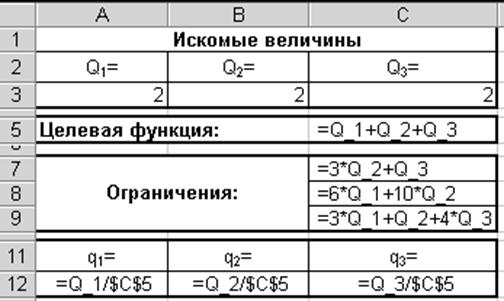
Рис. 1. Вихідні дані та формули для вирішення завдання

 Виконаємо команду Сервіс ► Пошук рішення і заповнимо вікно Пошук рішення згідно рис. 2.

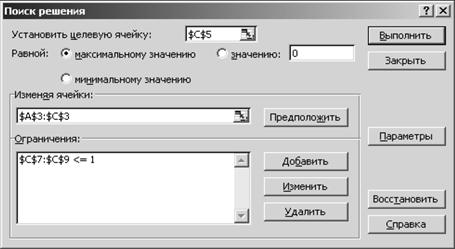
Рис. 2. Вікно Пошук рішення

 клацнемо на кнопку Параметри і у вікні Параметри пошуку вирішення встановимо прапорець невід'ємні значення.

 Виділимо діапазон комірок А12: С12 і виконаємо послідовність команд

Þ  Формат ►Ячеек ►Число ►Дробный ►Дробями до двух цифр.

У результаті розрахунків отримуємо, що Q1 = 0; Q2 = 0,1; Q3 = 0,225 та = 0,325. Таким чином, - оптимальна змішана стратегія гравця В. Оскільки гравець А має можливість обрати лише свою чисту стратегію, то його гру можна трактувати як гру з «природою». Застосуємо критерій Байеса-Лапласа. Для цього знайдемо середні значення виграшу Si для кожної чистої стратегії Ai:

 

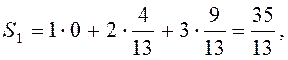
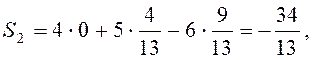
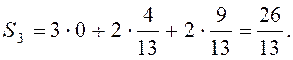
Так як, отже, перша стратегія є оптимальною.