Исследование основных характеристик измерительных органов тока, страница 2

          Поскольку амплитуды  и  равны и не зависят от частоты, векторы дополнительных сигналов всегда совпадают с диагоналями ромба, образованного  и , в связи с чем угол между векторами  и  составляет π/2 и не зависит от угла α между  и  , а следовательно, и от частоты входного сигнала.

Так как входной сигнал гармонический, то и дополнительные также гармонические:

;

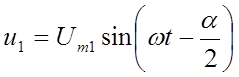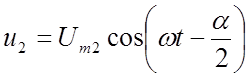,                                 (7.4)

где  и  —  амплитуды первого и второго дополнительных сигналов.

          Когда для двух смежных моментов времени  и  зафиксированы мгновенные значения сигналов (7.4), они будут связаны следующей системой соотношений:

;

;

;

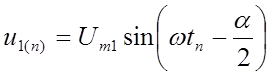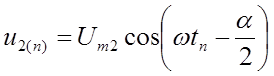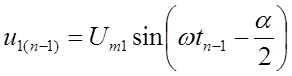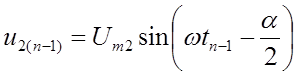.                            (7.5)

Из этой системы соотношений определим амплитуды дополнительных сигналов  и :

;

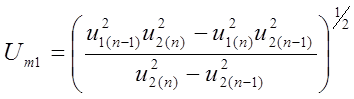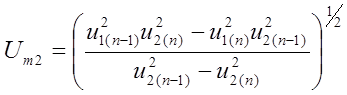                             .                           (7.6)

Амплитуда входного сигнала, как следует из векторной диаграммы (рис. 7.2), равна

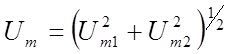                                         .                                   (7.7)

Подставив в (7.7)  и  получим

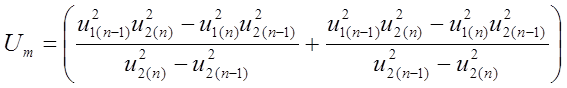           .         (7.8)

Из векторной диаграммы (рис. 7.2) следует, что:

;

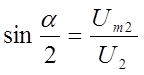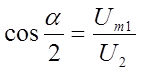                                             .                                           (7.9)

Подставив в (7.9) , и , будем иметь:

;

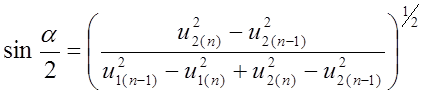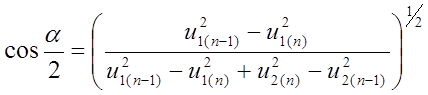.                  (7.10)

Подставим в первые два выражения (7.5) ,,, разрешим их относительно  и :

;

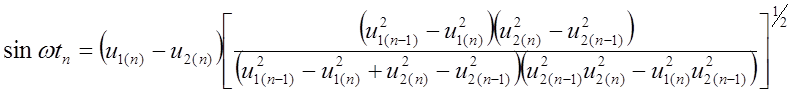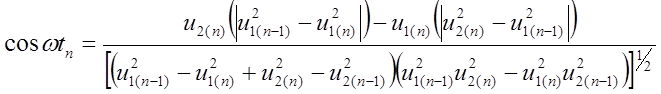 .    (7.11)

Известно, что отсчеты мгновенных значений синусной и косинусной ортогональных составляющих входного сигнала для момент времени  равны:

 

                                              .                                    (7.12)

Подставив в (7.12) ,,, после несложных преобразований получим:

;

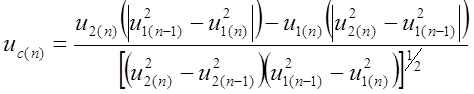.               (7.13)

Выражения (7.13) позволяют по двум отсчетам мгновенных значений сформированных дополнительных сигналов получить отсчеты мгновенных значений ортогональных составляющих входного синусоидального сигнала. При этом амплитуды ОС и угол фазового сдвига между составляющими не зависят от частоты входного сигнала. Данная независимость обеспечивается тем, что в выражение (7.13) входит в неявном виде информация о частоте.

Основные характеристики органов тока целиком и полностью определяются соответствующими характеристиками ИОТ, представленными на листе 4 графической части проекта.

В ИОТ формирование ортогональных составляющих входного сигнала осуществляется следующим образом: если входной сигнал содержит составляющие с частотами, отличными от промышленной, то он должен быть подвергнут частотной фильтрации с целью выделения основной гармоники. Для этого могут быть использованы соответствующие частотные фильтры. На основе анализа их АЧХ предпочтительным является фильтр,  реализованный с помощью выражения (6.2).

Цифровой отсчет вспомогательного сигнала, сдвинутого в сторону отставания на угол α без изменения амплитуды, может быть получен как

;                                    (7.14)

где i= 1 v 2 v ... v (n — 1).

С учетом (7.14) отсчеты первого и второго дополнительных сигналов формируются следующим образом:

;

.                             (7.15)

где i= 1 v 2 v ... v (n — 1).

Аналогичным образом получаются и смежные отсчеты дополнительных сигналов и . Следует отметить, что отсчеты выходного сигнала частотного фильтра являются в сущности отсчетами синусной ортогональной составляющей . Поэтому с помощью (7.13) достаточно формировать только отсчеты мгновенных значений косинусной ортогональной составляющей.

На плакате 4 представлены АЧХ частотно-независимых ИОТ, полученные расчетным путем на ПЭВМ. Их особенностью является полное совпадение АЧХ для синусной и косинусной ортогональных составляющих. Приведенные АЧХ по существу представляют собой характеристики соответствующих частотных фильтров. Наилучшую форму АЧХ с точки зрения подавления как апериодической составляющей, так и высших гармоник имеют ИОТ с n=6.

На этом же листе приведены переходные характеристики ИОТ и изменения амплитуды сигнала, представленного ортогональными составляющими, при подаче на вход синусоидального сигнала. Как видно из приведенных характеристик, время, необходимое для замера амплитуды сигнала при n = 5; 6; 7; 8, составляет 2,0; 2,2; 1,5; 1,65 периода основной частоты.

Для частотно-независимых ИОТ характерно возникновение интенсивного переходного процесса при подаче входного сигнала. Поэтому на отдельных интервалах времени не представляется возможным определить цифровой отсчет косинусной ортогональной составляющей.

Несмотря на это, частотно-независимые ИОТ могут быть отнесены к числу наиболее перспективных с точки зрения использования в РЗА.