Физические основы методов расчета режимов замкнутых электрических сетей. Основы расчетов режимов сложных электрических сетей на ПЭВМ

Глава 8. Физические основы методов расчета режимов замкнутых электрических сетей

8.1. Общие сведения о замкнутых электрических сетях и особенности их режимов

Замкнутыми сетями называются сети, в которых электроэнергия может протекать к потребителям по крайней мере с двух сторон (рис.8.1,а). Точки, к которым энергия может протекать по крайней мере с трех сторон, называются узловыми точками (рис. 8.1,б). Различают простые замкнутые сети, в которых присоединенные к ним нагрузки питаются не более чем с двух сторон, и сложные замкнутые сети, к узловым точкам которых электроэнергия может подаваться не менее чем с трех сторон.

Замкнутые электрические сети создают общность режима работы электростанций и сетей по производству и распределению электрической энергии. Это дает известные экономические выгоды. Однако при этом в эксплуатации электрохозяйства появляются свои сложности. Приходится решать вопросы надежности, качества электроэнергии, экономичности работы и др.

Распределение токов или мощностей в сложных замкнутых сетях может быть найдено решением уравнений, составленных по законам Кирхгофа и Ома.

Замкнутые сети встречаются не только в электроэнергетических системах, но в местных сетях. Поэтому с целью лучшего понимания методов расчета их режимов, рассмотрим эти методы сначала на примере местных сетей, а затем в данной главе более подробно изучим физические основы этих методов для сетей энергосистем.

Для получения меньшего числа уравнений существуют различные методы, из которых наиболее распространенными являются метод контурных уравнений и метод узловых уравнений.

Рассмотрим метод контурных уравнений на примере одного контура (рис. 8.1,а). На рис. 8.1,в дана векторная диаграмма, полученная при обходе контура.

Продольные и поперечные составляющие падения напряжения находятся по формулам:

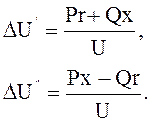
Так как многоугольник падений напряжений замкнутый, то можно написать, что суммы проекций векторов падений напряжений на горизонтальную и вертикальную оси равны нулю:

или

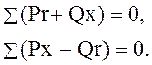
Для рис. 8.1 эти уравнения будут:

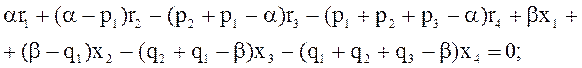
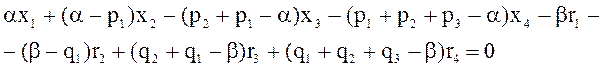или

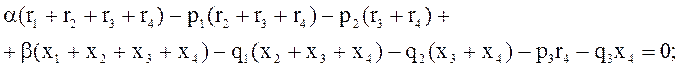
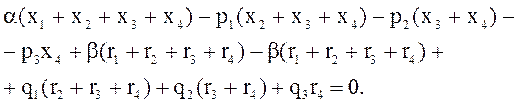
Обозначая:

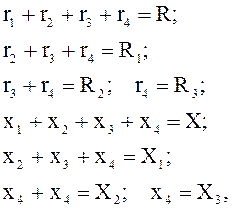получим:

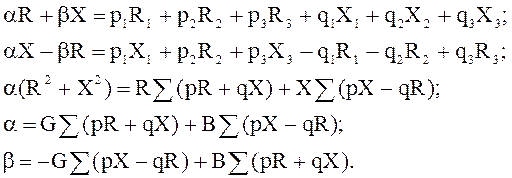
Аналогично можно получить формулы для активной  и реактивной  мощностей, выходящих из пункта А по направлению к точке 3:

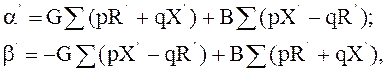где сопротивления  и , в данном случае, берутся от нагрузки до питательного центра в направлении часовой стрелки.

В методе узловых уравнений за неизвестные принимаются токи в ветвях и напряжения узлов. Для схемы (рис.8.1,б) неизвестными служат токи I_а, I_b и I_c, которые условно направляются на чертеже от узла к питательным пунктам, и напряжение узла U₀.

Для линий АО, ВО, СО, рассматривая их как линии с двусторонним питанием, можно написать (см. параграф 8.2):

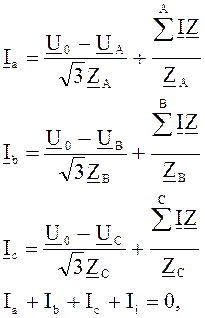                                    где U_A, U_B, U_C – линейные напряжения питательных пунктов А, В, С;

Z_A, Z_B, Z_C – cопротивления линий АО, ВО, СО;

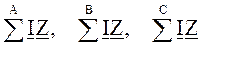‑ суммы произведений токов нагрузок на сопротивления от питательных пунктов до соответствующих нагрузок.

Решая эти уравнения найдем токораспределение в сети.

Расчеты установившихся режимов сложных электрических систем производятся в настоящее время на ЭВМ. Алгоритмы, реализованные в промышленных программах расчета установившихся режимов, основаны