Табл.5. Популяция на 20-ом поколении
Как видно из таблицы, все особи сошлись примерно к одной мелодии. В нашем случае это локальный оптимум, т.е. не идеал. Мутации происходили примерно у одной мелодии в поколении.
При 7 нотах в мелодии и 10 мелодиях в поколении получаются посредственные результаты. Для их улучшения необходимо увеличить количество нот и количество мелодий, как сделано в примере 2.
Количество нот в мелодии = 10 (количество бит = 40). Размер популяции = 20 особей. Вероятность мутации особей = 0.75. Вероятность мутации бита = 0.005 (общая вероятность мутации ноты = 0.015). Кроссовер одноточечный.
Рассмотрим для примера одну из мелодий, полученную в пятом поколении с фитнесс значением = 8.
Рис.2. Двоичный и символьный вид хромосомы
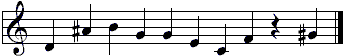
Рис.3. Нотная нотация хромосомы
Результаты в этом примере лучше, чем в предыдущем. Это, возможно, обуславливается тем, что качество мелодий легче определять на слух при 10 нотах, чем при 7.
Второе применение данного генератора - это создание обработок музыкальных произведений.
Возьмем в качестве входных данных фрагменты классического произведения Бетховена - “Лунная соната”. Выберем 8 фрагментов (из 24-х) по 12 нот, которые уместились в одну октаву. Все фрагменты транспонированы на 2 полутона вниз. Для улучшения результатов мелодии продублированы, т.е. количество особей = 16.
В качестве особенностей в этом случае необходимо отметить, что все фрагменты начальной популяции имеют одинаковое фитнесс значение (например, 5). Кроссовер двухточечный. Мутация не используется.
В результате скрещивания были получены, например, следующие мелодии:
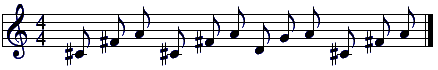
Рис. 4. Мелодия, полученная во втором поколении
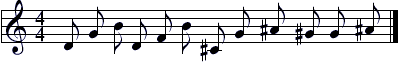
Рис.5. Мелодия, полученная в 3-м поколении
При объединении всех новых мелодий получается произведение в стиле “Лунной сонаты”, правда немного лишенной музыкального смысла.
Особенно необходимо отметить, что результаты получились бы лучше, если использовались бы все фрагменты произведения. Ограничение в возможности использования только 1-ой октавы уменьшило пространство поиска.
Программная реализация может работать в двух режимах: когда на вход подаются случайным образом сгенерированные ноты и когда подаются готовые фрагменты произведения для генерации новых фрагментов.
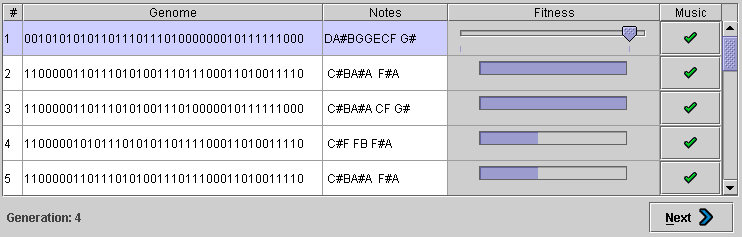
Рис.6. Главное интерактивное окно
Главная таблица состоит из колонок: хромосома; ноты, отображающие эту хромосому и ее фитнесс значение. Каждую хромосому можно прослушать через MIDI синтезатор и выставить ей оценку.
Всю популяцию возможно сохранить и затем загрузить. Мелодии можно сохранить в MIDI файлах. Также разрешено объединение мелодий популяции в одну большую композицию с ее последующим сохранением.
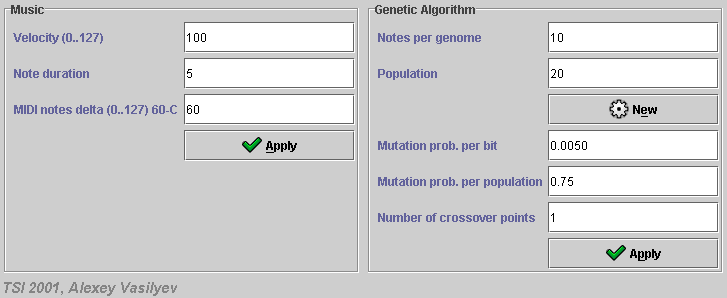
Рис.7. Настроечные параметры
В настройках параметров программы задается количество нот в
хромосоме (
, где 
- количество бит, 
- количество нот),
количество особей в популяции. Также задается вероятность мутации особей в
поколении и вероятность мутации одного бита (
,
где 
- общая вероятность мутации ноты, 
- вероятность мутации бита, 
- вероятность мутации особей),
количество точек сечения в
кроссовере.
Возможно изменение параметров, относящихся к прослушиваемой музыке: громкость, длительность ноты и корневая MIDI нота (60 - нота До первой октавы).
Применение в качестве оценочной фитнесс функции человека накладывает на данный алгоритм субъективность. Из-за его интерактивной итерационности ограничивается количество особей в поколении, поскольку при прослушивании большого числа мелодий наступает усталость. Помимо этого необходимо наличие музыкального слуха у пользователя. Для автоматизации вычисления фитнесс значения здесь возможно по крайне мере два способа: использование экспертной системы с правилами, описывающими гармонику нот (не все ноты могут друг с другом гармонировать), или натренированной нейро сети.
При формировании стохастически первой популяции для получения приемлемой “музыкальности” поколения необходимо некоторое количество утомительных итераций. В случае с уже заданными на вход мелодиями поколения всегда будут “музыкальными”. Хотя в первом случае иногда получаются мелодии гораздо интересней, нежели мелодии во втором случае.
Эволюционное программирование помимо музыки может еще использоваться в таком направлении искусства как живопись. Например, в работе NEvAr [8] использовались интерактивные алгоритмы, основанные на генетическом программировании (ГП) [9]. С их помощью формировались новые абстрактные картины, используя заданные абстрактные изображения.
Использование ГА в искусстве освобождает творческих личностей от генерации идей. Их помощь необходима только в отсечении нужных результатов, полученных с помощью эволюционного процесса. Однако необходимо отметить, что генетические алгоритмы не подходят идеально для генерации музыки, поскольку их операторы не эмулируют человеческий процесс создания музыки, хотя с их помощью и получаются довольно неплохие результаты. Хороших результатов можно достичь в области обработки музыкальных произведений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.