Расчет нелинейной цепи переменного тока (Задания на расчетно-графическую работу № 4)

Расчетно-графическая работа №4

РАСЧЕТ НЕЛИНЕЙНОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА

Исходные данные

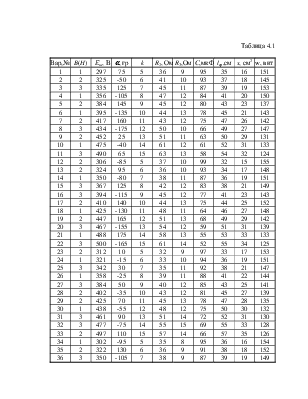
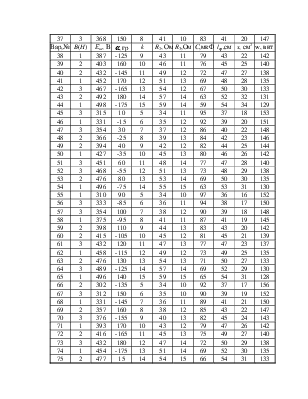
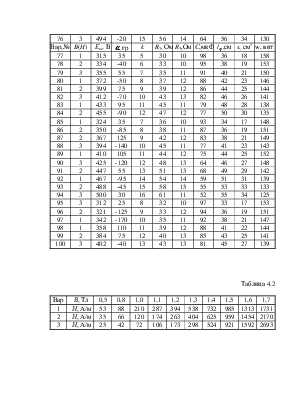
Схема нелинейной цепи (рис. 4.1) содержит источник ЭДС e(t)=E_m×sin(wt+a)[B], f=50 Гц, линейные элементы R₂[Ом], R₃[Ом], C[мкФ], нелинейный терморезистор с ВАХ U₁ =k×I₁² и нелинейную катушку с сердечником  из электротехнической стали. Параметры отдельных элементов схемы, геометрические размеры сердечника нелинейной катушки l[см], s[см²], её число витков  w[вит] заданы в табл. 4.1 согласно номеру варианта задания. Основная кривая намагничивания материала сердечника В=f(H) приведена в табл. 4.2. Сердечник имеет технологический зазор d= 0.1мм.

Содержание задания

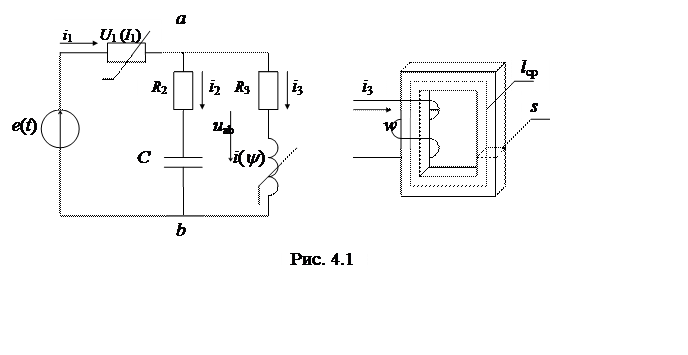
1) Рассчитать вебер-амперную характеристику i=f(y) нелинейной катушки, используя еe геометрические размеры и основную кривую намагничивания материала сердечника. Аппроксимировать вебер-амперную характеристику i=f(y) уравнением степенного полинома вида i=a×y+b×yⁿ, где i[A], y[Вб]. Коэффициенты аппроксимации a, b, n определить по методу выбранных точек. По результатам расчeта построить графическую диаграмму функции i=f(y) и нанести на полученную кривую расчетные точки этой характеристики.

2) Рассчитать вольт-амперную характеристику U=f(I) нелинейной катушки для действующих значений величин в режиме синусоидального напряжения u(t)=U_m×sin(wt)[B], f=50 Гц. Аппроксимировать вольт-амперную характеристику U=f(I) нелинейной катушки уравнением гиперболического синуса по форме I=с×sh(d×U), где I[A], U[B]. Коэффициенты аппроксимации с и d определить по методу выбранных точек. При расчете ВАХ использовать аппроксимацию i=a×y+b×yⁿ п. 1, потерями энергии в катушке пренебречь. По результатам расчeта построить графическую диаграмму функции I=с×sh(d×U) и нанести на полученную кривую расчетные точки этой характеристики..

3) Для расчетной схемы записать систему уравнений Кирхгофа в комплексной форме. Составить алгоритм решения полученной системы уравнений методом последовательных приближений вручную (на калькуляторе) и выполнить решение с относительной погрешностью не более 3%. В расчете использовать аппроксимацию вольтамперной характеристики п. 2. В результате расчета определить действующие значения токов I₁, I₂, I₃ и напряжения между узлами U_ab.

4) Решить систему уравнений Кирхгофа на ЭВМ по программе “Given...Find” и определить действующие значения токов I₁, I₂, I₃ и напряжения между узлами U_ab.. Результаты расчетов по двум методам свести в общую таблицу. По результатам расчета в выбранных масштабах построить векторные диаграммы токов и напряжений.

5) Для расчетной схемы составить систему дифференциальных уравнений по законам Кирхгофа, в которых использовать аппроксимацию вебер-амперной характеристики катушки уравнением степенного полинома i=a×y+b×yⁿ (п. 2). Выполнить решение системы дифференциальных уравнений на ЭВМ по программе rkfixed в интервале времени 5Т. В выбранных масштабах m_u и m_i построить графические диаграммы функций токов i₁(t), i₂(t), i₃(t) и напряжения между узлами u_ab(t)  в интервале времени 3Т.

6)  В выбранном масштабе построить для сравнения совмещенную графическую диаграмму тока катушки i₃=f(t) в переходном (1+2-й периоды) и в установившемся (4+5-й периоды) режимах. По диаграмме определить время переходного процесса Тпп.

7) Для функций i₁(t), i₂(t), i₃(t), u_ab(t) определить действующие значения величин I₁, I₂, I₃, U_ab. Результаты расчетов п.п. 4 и 7 свести в общую таблицу для сравнения.

8) Для функции i₃(t) определить также максимальное значение I_3max, среднее значение I_3ср,   амплитуды и начальные фазы гармоник (до 7-ой включительно). Записать выражение исследуемой  функции i₃(t)  в форме гармонического ряда Фурье. Для функций i₃(t) определить коэффициенты, характеризующие форму кривой: k_г -коэффициенты 3-й, 5-й и 7-й гармоник, k_и - коэффициент искажения, k_а - коэффициент амплитуды, k_ф - коэффициент формы кривой.

Таблица 4.1