Исследование простых нелинейных цепей постоянного тока (Лабораторная работа № 23Н)

Л а б о р а т о р н а я   р а б о т а  № 23Н

ИССЛЕДОВАНИЕ ПРОСТЫХ НЕЛИНЕЙНЫХ ЦЕПЕЙ

ПОСТОЯННОГО ТОКА

23.1. Цель работы

1. Изучение графических и аналитических методов расчета простых нелинейных цепей постоянного тока с применением вольт-амперных характеристик (ВАХ) нелинейных элементов.

2. Экспериментальное исследование нелинейных цепей с заданными параметрами элементов с целью установления соответствия между результатами расчета и эксперимента.

23.2. Исходные данные

Заданы:

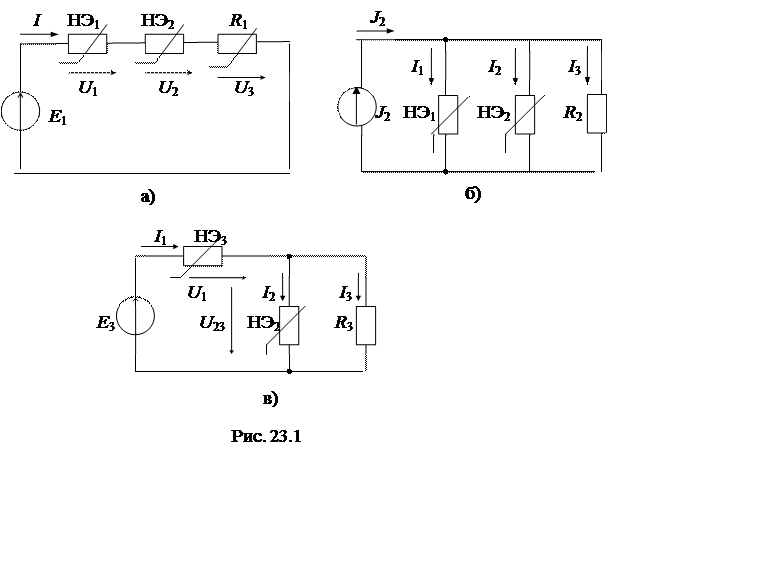
1. Эквивалентные схемы исследуемых нелинейных цепей (рис. 23.1а,б,в).

2. Параметры элементов схем (табл. 23.1). Вольт-амперные характеристики нелинейных резисторов заданы уравнениями: для  НЭ₁  U₁ = a₁∙I₁², для  НЭ₂  U₂ = a₂∙I₂²,для  НЭ₃  I₃ = a₃∙U₃². Коэффициенты уравнений заданы в табл. 23.2.

3. Рабочие схемы исследуемых цепей и схемы включения измерительных приборов (рис. 23.2  - 23.4).

Т а б л и ц а   23.1

Вариант	1	2	3	4	5	6	7	8	9	10
Е1, В	100	90	100	110	120	85	95	105	115	120
Е3, В	70	80	90	100	110	75	85	95	105	115
J, A	1,40	1,50	1,60	1,70	1,80	1.45	1,55	1,65	1,75	1,85
R1, Ом	50	90	100	110	120	85	95	105	115	125
R2, Ом	90	100	110	120	130	95	105	115	125	135
R3, Ом	70	75	80	85	90	55	80	85	90	95

Т а б л и ц а  23.2

К-ты ур-ний.	а1	а2	a3
Задано	60	100	1,3∙10-3

 

23.3. Теоретические сведения и методические указания

Нелинейными элементами (НЭ) электрической цепи постоянного тока называются такие элементы, для которых вольт-амперные характеристики  U(I) или I(U) являются нелинейными и не могут быть описаны линейным уравнениями U=IR. Вольт-амперные характеристики  нелинейных элементов U(I) или I(U)  могут быть представлены тремя способами: а)в графической форме – в  виде графических диаграмм функций U(I) или I(U), б)в табличной форме – виде таблиц координат точек функций U(I) или I(U), в)в математической форме – в виде нелинейных алгебраических уравнений, описывающих функции U(I) или I(U).

Нелинейной называется электрическая цепь (схема), которая в своей структуре содержит нелинейные элементы. Физические процессы в нелинейной цепи постоянного тока можно описать системой нелинейных алгебраических уравнений, составленных для схемы цепи по законам Кирхгофа. В математике нет универсальных  методов решения систем нелинейных уравнений, поэтому не существует универсальных  методов расчета нелинейных цепей постоянного тока. Выбор метода расчета конкретной  нелинейной цепи определяется индивидуально исходя из заданных условий. Применяются графические, аналитические, численные и комбинированные методы расчета.

Сущность графического метода расчета состоит в том, что решение нелинейных уравнений, составленных для схемы по законам Кирхгофа, выполняется путем графического сложения соответствующих вольт-амперных характеристик элементов.              

При последовательном включении элементов уравнения Кирхгофа имеют вид:  U₁ + U₂ + U₃= E;      I₁ = I₂ = I₃ = I.

В соответствии с уравнениями производится сложение вольт-амперных характеристик  отдельных элементов U₁(I), U₂(I) и U₃(I)  по оси напряжений (последовательно), в результате чего получается вольт-амперная характеристика для всей схемы U(I). На этой вольт-амперной характеристике для значения U=E определяется положение рабочей точки n. Последовательность графического решения показана на рис. 23.2 стрелками.

Рис. 23.2

Численное решение нелинейного уравнения, дополненного уравнениями аппроксимации,  может быть выполнено на ЭВМ по программе “Given … Find”:

При параллельном включении элементов уравнения Кирхгофа имеют вид:

I₁ + I₂ + I₃ = J;       U₁ = U₂ = U₃ = U.

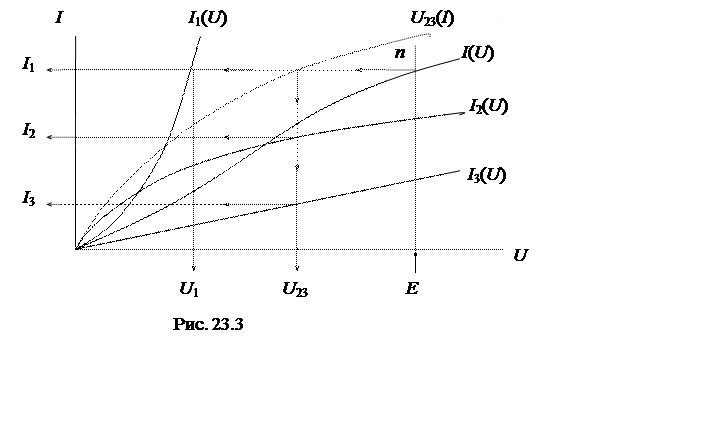
В соответствии с уравнениями производится сложение вольт-амперных характеристик отдельных элементов I₁(U), I₂(U) и I₃(U)    по оси токов (параллельно), в результате чего получается вольт-амперная характеристика для всей схемы I(U) . На этой ВАХ для заданного значения I=J определяется положение рабочей точки  n. Последовательность графического решения показана на рис. 23.3  стрелками.

Рис. 23.3

Численное решение нелинейного уравнения, дополненного уравнениями аппроксимации,  может быть выполнено на ЭВМ по программе “Given … Find”:

При включении элементов по смешанной схеме уравнения Кирхгофа имеют вид:

; ; .

Графическое решение этих уравнений выполняется в два этапа. На 1-ом этапе проводится сложение вольт-амперных характеристик  I₂(U₂) и I₃(U₃) по оси токов (параллельно), в результате этого сложения получается  вольт-амперная характеристика  для параллельного участка схемы U₂₃(I₁). На 2-ом этапе проводится сложение вольт-амперных характеристик U₁(I₁)  и U₂₃(I₁) по оси напряжений (последовательно), в результате чего получается вольт-амперная характеристика  для всей схемы I(U). На этой характеристике для U=Е определяется положение рабочей точки n. Дальнейшая последовательность графического решения показана на рис. 23.3 стрелками.