Исследование сложной цепи переменного тока (Лабораторная работа по ТОЭ № 5БН)

Министерство образования Республики Беларусь

Кафедра “Электротехника и электроника”

Лабораторная работа по ТОЭ №5БН

ИССЛЕДОВАНИЕ СЛОЖНОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА

М и н с к    2 0 10

Л а б о р а т о р н а я   р а б о т а   № 5БН

ИССЛЕДОВАНИЕ СЛОЖНОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА

5.1. Цель работы

1.   Изучение методов расчета схем сложных цепей переменного тока.

2.   Теоретическая и экспериментальная проверка баланса токов в узлах цепи согласно 1-му закону Кирхгофа и баланса напряжений в контурах согласно 2-му закону Кирхгофа.

3. Изучение методов измерения комплексных напряжений и потенциалов точек в  сложной цепи переменного тока.

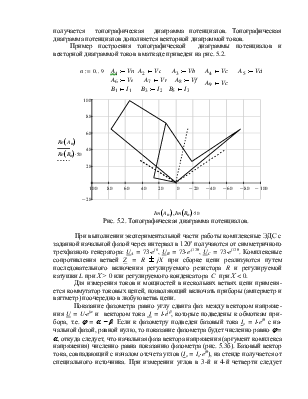
4. Изучение методов построения топографической диаграммы потенциалов и векторной диаграммы токов  для  сложной схемы.

5.2. Исходные данные

Заданы:

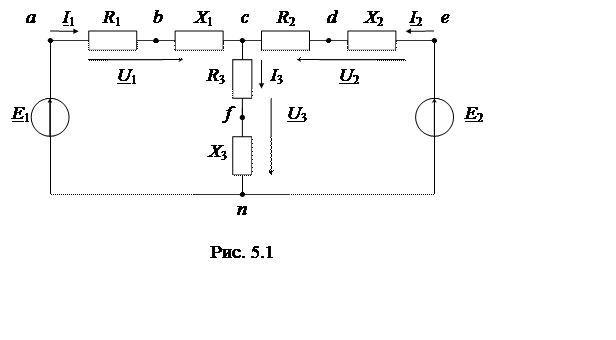
1. Эквивалентная схема исследуемой сложной цепи (рис. 5.1).

2. Параметры элементов схемы в комплексной форме: E = Е×е^ja, Z=R + jX(табл. 5.1).

3. Рабочая схема исследуемой цепи (рис. 5.3) и схемы включения измерительных приборов (рис. 5.4).

Т а б л и ц а   5.1.

5.3.Теоретические сведения и методические указания

Электрическое состояние любой сложной схемы (цепи) определяется системой уравнений, составленных для нее  по 1-му и 2-му законам Кирхгофа в комплексной форме.

1-ый  закон Кирхгофа: алгебраическая сумма комплексных токов в узле схемы (цепи) равна нулю, или åI=0.

2-ой  закон Кирхгофа: алгебраическая сумма комплексных падений напряжений в замкнутом контуре схемы (цепи) равна алгебраической сумме комплексных ЭДС, или åU=åE.

Для любой сложной схемы в соответствии с законом сохранения энергии должен выполняться баланс (равенство) отдельно для активных  мощностей источников и приемников энергии SР_ист= SР_пр, и отдельно для реактивных  мощностей источников и приемников энергии SQ_ист= SQ_пр.

При расчете схемы в комплексной форме за базовый вектор (начало отсчета значений углов) рекомендуется принять фазное напряжение фазы А в трехфазной системе, т. е.  U_A = U_ф×e^j0.

Расчет токов в сложной схеме с двумя комплексными источниками ЭДС  следует выполнить одним из методов расчета сложных схем по выбору (метод законов Кирхгофа, метод контурных токов, метод двух узлов), при этом уравнения следует составлять в комплексной форме.

Система уравнений Кирхгофа:

I₁ + I₂ – I₃ = 0

I₁·Z₁ + I₃·Z₃ = E₁

I₂·Z₂ + I₃·Z₃ = E₂

В результате решения системы уравнений определяются комплексные токи ветвей  I₁,  I₂,  I₃.

Пример решения системы комплексных уравнений Кирхгофа в маткаде приведен ниже.

Система контурных уравнений:

Ik₁·(Z₁ + Z₃) + Ik₂·Z₃ = E₁

Ik₂·(Z₂ + Z₃) + Ik₁·Z₃ = E₂

В результате решения системы уравнений определяются комплексные контурные токи  Ik₁,  Ik₂. Токи ветвей  I₁,  I₂,  I₃  определяются через контурные токи:  I₁ = Ik₁, I₂ = Ik₂, I₃ = Ik₁ + Ik₂.

Уравнение метода 2-х узлов:

 .

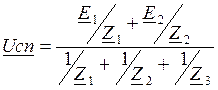Токи ветвей  I₁,  I₂,  I₃  определяются из потенциальных уравнений ветвей:

;             ;                      .

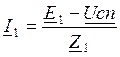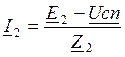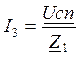Напряжения на отдельных участках схемы определяются по закону Ома:

U₁ = I₁·Z₁,   U₂ =  I₂·Z₂,   U₃  = I₃·Z₃.

Активные и реактивные мощности отдельных источников и приемников энергии определяются в комплексной форме:

S_E1 = P _E1 + jQ _E1 = E₁·I₁^*,   S_E2 = P _E2 + jQ _E2 = E₂·I₂^*,  S₁ = P ₁ + jQ ₁ = U₁·I₁^*, 

S₂ = P ₂ + jQ ₂ = U₂·I₂^*,  S₃ = P ₃ + jQ ₃ = U₃·I₃^*. 

Состояние электрической цепи можно описывать потенциальной функцией, разность значений потенциалов в двух заданных точках численно равна напряжению между этими точками: Uab = Va–Vb. При расчете потенциалов точек схемы потенциал одной из них принимают равным нулю, а потенциалы остальных определяют через напряжение между двумя любыми