Исследование форм кривых напряжений в нелинейной цепи переменного тока (Лабораторная работа № 27Н)

Министерство образования Республики Беларусь

 

Кафедра “Электротехника и электроника”

Лабораторная работа по ТОЭ №27Н

ИССЛЕДОВАНИЕ ФОРМ КРИВЫХ НАПРЯЖЕНИЙ В НЕЛИНЕЙНОЙ  ЦЕПИ ПЕРЕМЕННОГО ТОКА

М и н с к    2 0 10

Л а б о р а т о р н а я   р а б о т а  №27

ИССЛЕДОВАНИЕ ФОРМ КРИВЫХ НАПРЯЖЕНИЙ В НЕЛИНЕЙНОЙ  ЦЕПИ ПЕРЕМЕННОГО ТОКА

27.1. Цель работы

1. Изучение методов расчета нелинейных цепей переменного тока в установившемся режиме на основе численного интегрирования дифференциальных  уравнении Кирхгофа на ЭВМ в MathCAD.

2. Исследование характера и степени искажения форм кривых напряжений на элементах феррорезонансной цепи.

3. Теоретическое определение интегральных параметров, характеризующих несинусоидальные функции времени.

4. Экспериментальное измерение интегральных параметров, характеризующих несинусоидальные функции времени

27.2. Исходные данные

Заданы:

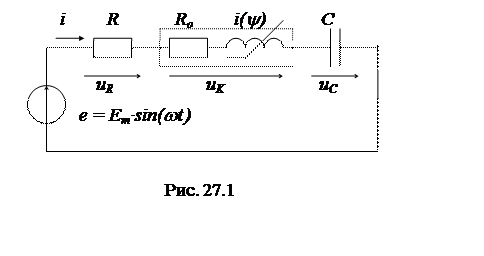
1. Эквивалентная схема исследуемой цепи (рис. 27.1), состоящая из  последовательно включенных источника синусоидальной ЭДС e(t) = E_m·sin(wt),нелинейной катушки [R₀, i(y)], линейного резистора R и конденсатора С.

2. Параметры линейных элементов (табл. 27.1). Нелинейная катушка на схеме представлена двумя схемными элементами, включенными последовательно - линейным резистором R₀и идеальной нелинейной катушкой с вебер-амперной характеристикой i(y) = a·sinh(b·y). Коэффициенты аппроксимации ВбАХ a и b заданы в табл. 27.1.

3. Рабочая схема исследуемой цепи и схемы включения измерительных приборов (рис. 27.4).

 

Т а б л и ц а   27.1

Вариант	1	2	3	4	5	6	7	8	9	10
Еm, В	75	80	85	70	75	85	80	75	85	80
R, Ом	30	35	40	35	40	45	35	40	50	45
R0, Ом	2	3	4	2	3	4	2	3	4	3
C,мкФ	60	55	45	65	60	40	55	50	40	50
Выводы	0-2	0-3	0-4	0-2	0-3	0-4	0-2	0-3	0-4	0-3
а	0,116	0,085	0,068	0,116	0,085	0,068	0,116	0,085	0,068	0,085
в	10,6	9,5	8,4	10,6	9,5	8,4	10,6	9,5	8,4	9,5

27.3. Теоретические сведения и методические указания

Физические процессы в нелинейной цепи переменного тока можно описать системой нелинейных дифференциальных уравнений, составленных для схемы цепи по законам Кирхгофа и дополненной  нелинейными алгебраическими уравнениями аппроксимации физических характеристик нелинейных элементов. Для исследуемой схемы эта система имеет вид:

i ·R +  i·R₀ + +u_С =  e(t )(1)

i = C·                                          (2)

i = a·sinh(b·y).                                    (3)

Решение системы дифференциальных уравнений может быть выполнено на ЭВМ методом численного интегрирования  по стандартной программе rkfixed (метод Рунге-Кутта 4-го порядка с фиксированным шагом интегрирования). Для этого исходную систему уравнений сначала преобразуется к стандартной форме (Коши), а затем решается по стандартной программе.

= (R+·R₀) · a·sinh(b·y) − u_С + e(t )

= (1/C) · a·sinh(b·y)

Результатом решения системы дифференциальных уравнений являются массивы значений (матрицы) переменных величин в интервале интегрирования (5 периодов или 0,1с). Далее на примере функции i(t) выполняется необходимая для решения задачи математическая обработка полученных массивов. Для дальнейшей обработки используются данные 3-го периода (исключается интервал времени с переходным процессом). Строятся графические диаграммы исследуемых функций, определяются их максимальные, действующие и средние (по модулю) значения. Вычисляются действующие значения основных и высших гармоник. Определяются коэффициенты, характеризующие несинусоидальные функции: Ka, Kф, Kи.

Рис. 27.2. Графические диаграммы функций e(t), uc(t), uk(t), ur(t).

Формулы для расчета интегральных параметров функций приведены ниже на примере функции тока i(t).

1) Максимальные значения функций:

2) Действующие значения функций:

3) Средние значения функций:

4) Комплексные действующие значения основных гармоник функций:

5) Действующие значения высших гармоник функций:

6) Коэффициенты амплитуды функций:

7) Коэффициенты формы функций:

8) Коэффициенты искажения функций:

Метод численного интегрирования (численный метод) обладает высокой точностью, так как в нем непосредственно используются физические характеристики нелинейных элементов. С появлением ЭВМ и расширением области их применения данный метод является основным при расчете нелинейных цепей как в установившемся, так и в переходном режиме.

При выполнении экспериментальной части работы максимальные, действующие и средние (по модулю) значения несинусоидальных напряжений измеряются каждое специальными вольтметрами. Для измерения действующих  значений основной гармоники напряжений в настоящей лабораторной