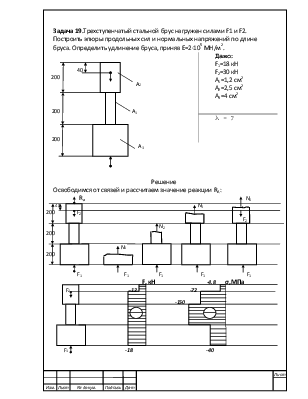





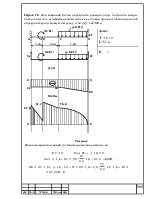











Задача 19.Трехступенчатый стальной брус нагружен силами F1 и F2. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить удлинение бруса, приняв Е=2·105 МН/м2.
|
Дано: F1=18 кН F2=30 кН A1=1,2 см2 A2=2,5 см2 A3=4 см2 |
|
λ - ? |
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]() 40
40
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]() 200
200
А2
200 А1
200
А3
Освободимся от связей и рассчитаем значение реакции RA:
Ra N4
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()

![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
 40 N3
40 N3
![]()
![]()
![]()
![]()
![]() 200
F2
200
F2
F2
![]()
![]()
![]()
![]() N2
N2
![]()
![]()
![]() 200
200
N1
200
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()

![]() F1 F1 F1 F1 F1
F1 F1 F1 F1 F1
![]()
![]()
![]() F, кН
-4.8 σ,МПа
F, кН
-4.8 σ,МПа
![]()
![]()
![]()
![]() F2
-12
-72
F2
-12
-72
![]()
![]() -150
-150
 |
|||||||
F1 -18 -40
![]()
![]()
Мысленно разобьем брус на четыре участка AB,BC,CD,DE,расположив граничные точки в местах изменения диаметра бруса и в местах приложения сил. На каждом из участков мысленно проведем сечения I,II,III,I٧, и рассмотрим каждое из этих сечений.
I: N1+F1=0 N1=-F1=-18кН;
II: N2+F1=0 N2=-F1=-18кН;
III: N3+F1=0 N3=-F1=-18кН;
IV: N4+F1-F2=0 N4=F2-F1=30-18=-12кН;
Как видим, усилие N4=RA, что подтверждает правильность наших расчетов.
Построим эпюру продольных сил, возникающих в брусе. ( См. рис. выше)
Определим нормальные напряжения σ, возникающие в сечениях.
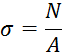
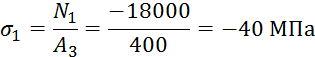
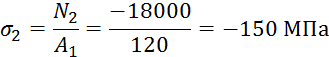
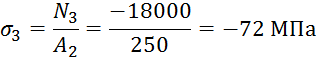
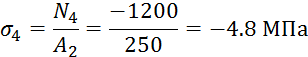
Теперь построим эпюру нормальных напряжений, возникающих в сечениях бруса ( см. рис. выше).
Судя по знакам посчитанных продольных усилий, можно утверждать, что стержень растянут. Определим его удлинение λ, которое найдем как сумму удлинений участков.
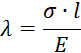
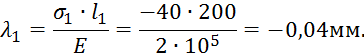
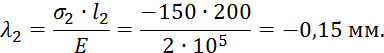
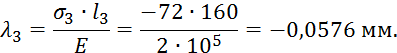
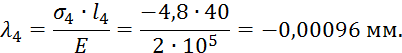
![]()
Ответ:![]()
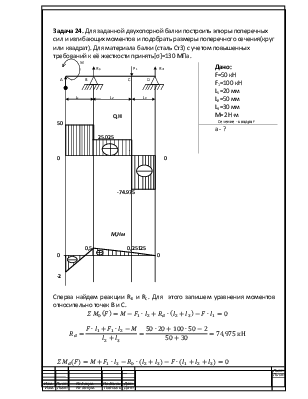
 Задача 24. Для заданной двухопорной балки построить эпюры
поперечных сил и изгибающих моментов и подобрать размеры поперечного
сечения(круг или квадрат). Для материала балки (сталь Ст3) с учетом повышенных
требований к её жесткости принять[σ]=130 МПа.
Задача 24. Для заданной двухопорной балки построить эпюры
поперечных сил и изгибающих моментов и подобрать размеры поперечного
сечения(круг или квадрат). Для материала балки (сталь Ст3) с учетом повышенных
требований к её жесткости принять[σ]=130 МПа.|
Дано: F=50 кН F1=100 кН L1=20 мм L2=50 мм L3=30 мм M=2 Н∙м Сечение - квадрат |
|
а - ? |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() M
M
![]() Rb F1 Rd
Rb F1 Rd
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() A B C D
A B C D
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() L1
L2 L3
L1
L2 L3
Q,H
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 50
50
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 25.025
25.025
0 0
![]() -74.975
-74.975
M,Нм
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0,5 0,25125
0,5 0,25125
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 00
00
-2
Сперва найдем реакции RB и RC. Для этого запишем уравнения моментов относительно точек B и C.
![]()
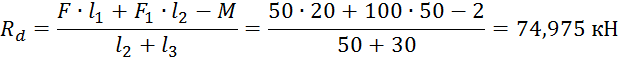
![]()
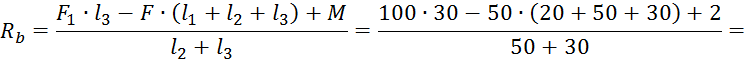
=-24,975 кН
Проверка: ![]()
![]()
Построим эпюру поперечных усилий Q. Для это найдем поперечные усилия в критических точках A,C,D,B с учетом правила знаков.
![]()
![]()
![]()
![]()
Построим эпюру изгибающих моментов Мх.
![]()
![]()
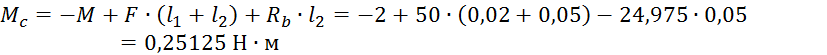
В данной задаче нам необходимо произвести проектный расчет для нахождения диаметра сечения бруса.
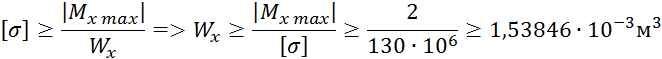
![]()
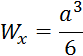
![]()
Ответ: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()



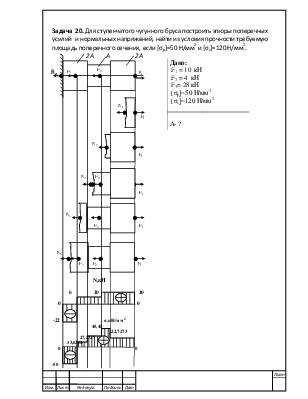
![]() 2A A 2A
2A A 2A
|
Дано: F1 = 10 кН F2 = 4 кН F3= 28 кН [σр]=50 Н/мм2 [σс]=120 Н/мм2 |
|
|
А- ? |
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Ra F1
Ra F1
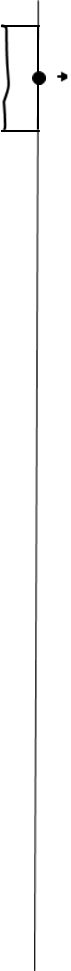 |
||||||||||||
N1
F1
 |
N2
F1
 |
|||||||||
N3 F2
![]()
![]()
F1
 |
|||||

N4
F2 F1
 |
 |
||||

N5
F3 F2 F1
N,кН
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 6 10 10
6 10 10
 |
|||
![]()
![]()
![]()
![]() 0 0
0 0
![]() -22 σ,кН/мм2
-22 σ,кН/мм2
![]()
![]()
![]()
![]()
![]() 45,45
45,45
22,7273
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 27,2727
27,2727
![]()
![]()
![]()
![]()
![]() 13,6364
13,6364
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0 0
0 0
![]() -50
-50
Решение
Исходя из уравнений равновесия для каждого сечения, найдем усилия
N1, N2, N3, N4, N5:
![]()
![]()
![]()
![]()
![]()
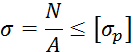
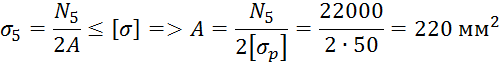
![]()
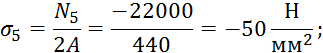
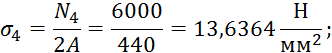
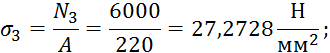
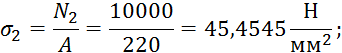
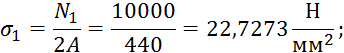
Отметим, что максимальные напряжения на участках удовлетворяют условиям прочности.
Ответ: А=220 мм2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() F1
F1
|
Дано: F = 15 кН F1=40 кН М = 15 кН·м [σ]=160 МПа h/b=2 L1=0,4 м L2=0,3 м L3=0,3 м |
|
|
Cечение, эпюры ? |
|
M
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() A B F C D
A B F C D
![]()
![]() L3 L2 L1
L3 L2 L1
![]()
![]()
![]()
 |
![]()
![]()
![]() Ma F1
Ma F1
![]()
![]() Ra
Ra
F M
Q, кН
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 25
25
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0
0
0
0
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -15 -15
-15 -15

![]() 36
36
![]() M,кНм
M,кНм
![]()
![]()
![]()
![]() 0 0
0 0
![]()
10,5
15 15
Решение
Освобождаемся от связей, обозначая реакции. В точке A—глухая заделка, поэтому кроме реакции Ra, направленной вертикально, здесь будет еще и момент Мa.
Из уравнений равновесия определим реакции:
![]()
![]()
![]()
![]()
Зная реакции, можно определить поперечные силы в балке:
![]()
![]()
![]()
![]()
Строим эпюру поперечных напряжений.
Определим изгибающие моменты в характерных точках:
![]()
![]()
![]()
![]()
![]()
Строим эпюру изгибающих моментов.
Для того, чтобы подобрать размеры поперечного сечения, запишем условие прочности:
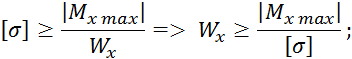
![]()
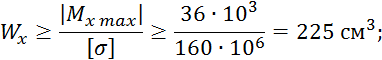
Рассмотрим случай двутавра:
По табл. находим ближайшее большее значение WX=232,0 см3, которому соответствует балка № 22.
Рассмотрим случай прямоугольника:
WX в этом случае вычисляется по формуле:
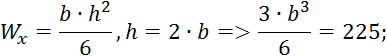
![]()
![]()
Ответ: h=![]() балка № 22.
балка № 22.
Задача 25. Для заданной балки определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и из условия прочности балки на изгиб определить допускаемую нагрузку, если [σ] = 100 МПа.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() q=0,8F/l
q=0,8F/l
|
Дано: F =10 кН L=0,3 м |
|
|
RA – ? |
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() M=6Fl
M=6Fl
![]()
![]()
![]()
![]() 8F
8F
A B C D
0,3м 0,3м 1,2м
M=6Fl q=0,8F/l
Ra 8F
Q,кН
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0 0
0 0
![]()
![]() 48
48
48
48
80
М,кНм

![]()
![]()
![]()
![]()
![]()
![]()
![]() 91,2
76,8
91,2
76,8
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 87,6
87,6
![]() 0 0
0 0
Решение
Для нахождения реакций составим уравнения равновесия:
![]()
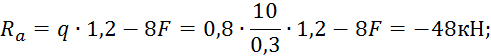
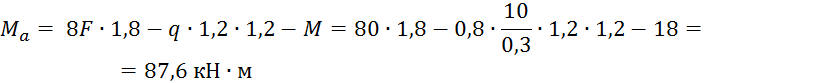
Зная реакции, можно определить поперечные силы в балке:
![]()
![]()
![]()
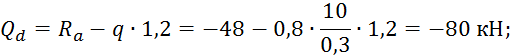
Строим эпюру поперечных напряжений.
Определим изгибающие моменты в характерных точках:
![]()
![]()
![]()
![]()
Строим эпюру изгибающих моментов.
По табл. берем Wx , затем определяем допускаемую нагрузку.
![]()
![]()
![]()
Ответ:![]()
![]()
Решение.
1. Составляем таблицы механических характеристик составных частей провода и исходных данных.
Механические характеристики составных частей провода
|
Модуль упругости, Н/мм2 |
Коэффициент расширения, 1/град |
Предел прочности, Н/мм2 (МПа) |
Удельные веса, Н/см3 = Н/м×мм2 |
||||
|
ЕА |
ЕС |
aА |
aС |
|
|
gА |
gС |
|
7×104 |
21×104 |
25×10-6 |
12,5×10-6 |
200 |
800 |
27×10-3 |
78×10-3 |
Исходные данные
|
Сечение |
Длина |
Температура |
Отношение площадей |
Отношение нагрузки |
Запас прочности |
Площади сечений |
||
|
А, мм2 |
l, м |
t1° |
t2° |
АА/AC |
k1 = g2/g1 |
[S] |
АА |
АC |
|
300 |
300 |
15 |
-12 |
7,5 |
1,75 |
2,5 |
260 |
40 |
2. Определяем приведенные величины биметаллического провода по формулам. Причем для ускорения вычислений эти формулы следует упростить, разделив числители и знаменатели некоторых формул на АС, а одну из формул – на произведение ЕС×АС и вводя при этом коэффициенты
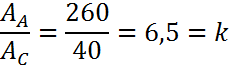
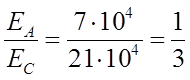 .
.
При вычислении приведенных величин особое внимание следует уделить их наименованию и размерностям.
![]() ;
;
![]() ;
;
![]() ;
;
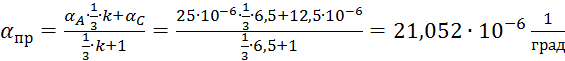 .
.
3. По результатам приведенных величин и формулам последовательно получаем вспомогательные коэффициенты:
g2 = k1×g1 = 1,75× 33,8 10-3 = 59,15 10-3 ![]() ;
;
![]() ;
;
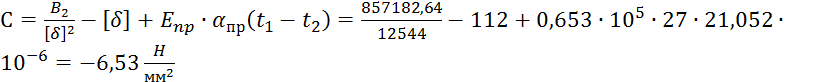 ;
;
![]() ;
;
4. По результатам расчетов приведенных величин составляем табл.
Приведенные величины
|
Епр, МПа |
g1, Н/м×мм2 |
[s], МПа |
aпр, град-1 |
B1, (МПа)3 |
С, МПа |
|
|
33,8×10-3 |
112 |
|
|
|
Найденные числа позволяют составить «уравнение состояния провода
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.