Задача 1
Предприятие получило кредит в размере 10 млн.р. сроком на 1 год с условием возврата 15 млн.р. Определить сложную и простую процентные ставки.
Решение:
Определим простую процентную ставку
Пусть Р – первоначальная сумма, S – наращенная сумма, i – годовая процентная ставка (проценты простые). Так как проценты простые, то в течение всего периода начисления они применяются к первоначальной сумме Р.
Наращенную сумму спустя год можно определить по формуле:
![]()
Отсюда можно определить простую процентную ставку:
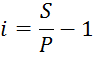
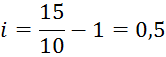
Простая процентная ставка составляет 50%.
Определим сложную процентную ставку
Пусть Р – первоначальная сумма, S – наращенная сумма, i – годовая процентная ставка (проценты сложные). Так как проценты сложные, то в конце каждого интервала начисления процентная ставка применяется к наращенной сумме на начало этого интервала начисления.
Наращенная сумма по сложной процентной ставке, спустя год определяется по формуле:
![]()
Таким образом, сложная и простая процентные ставки спустя год равны.
Сложная процентная ставка составляет 50%.
Задача 2
Найти возвращаемую сумму, если взятая ссуда составляет 220 тыс.р., а срок ее погашения равен 3 года. Контрактом предусмотрена сложная процентная ставка в размере 19% годовых. Начисление процентов производится ежеквартально.
Решение:
Начисление сложных процентов может происходить несколько раз в году. В этом случае указывают номинальную процентную ставку j, на основании которой рассчитывают процентную ставку для каждого интервала начисления.
Если в году m интервалов начисления, то в каждом из них процентная ставка равна j/m. Тогда наращенная сумма рассчитывается по формуле:
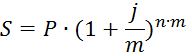
Поскольку начисление процентов производится ежеквартально, то m=4.
Определим возвращаемую сумму:
![]() тыс.р.
тыс.р.
Возвращаемая сумма составляет 383,946 тыс.р.
Задача 3
Проведите анализ двух вариантов накопления средств по схеме аннуитета постнумерандо:
Вариант 1. Каждые полгода вносится вклад по 15 тыс.р. При условии, что банк начисляет 8% годовых с полугодовым начислением сложных процентов;
Вариант 2. Делается ежегодный вклад в размере 30 тыс.р. при начислении 10% годовых ежегодно.
Требуется определить величины накопленной суммы через 10 лет в каждом варианте. Какой из этих вариантов более предпочтителен? Изменится ли ваше предпочтение, если процентная ставка в варианте 2 изменится до 9%.
Решение:
Большинство современных коммерческих операций основано не на разовых платежах, а на последовательности денежных поступлений в течение определенного периода. Например, поток однонаправленных платежей с равными интервалами в течение определенного количества лет называется аннуитетом, т.е. финансовой рентой.
Пусть R – ежегодные платежи, на которые начисляются
проценты в конце каждого года по сложной процентной ставке i, n – срок ренты. Платеж в конце первого
года даст наращенную сумму ![]() Платеж в конце 2 – го
года даст наращенную сумму
Платеж в конце 2 – го
года даст наращенную сумму![]() . Платеж в конце 3 –
го года даст наращенную сумму
. Платеж в конце 3 –
го года даст наращенную сумму ![]() . Итак далее.
Наращенная (будущая) сумма ренты:
. Итак далее.
Наращенная (будущая) сумма ренты:
![]()
Мы получили сумму n первых членов геометрической прогрессии
с ![]()
Тогда:
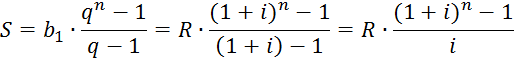
Рассчитаем величину накопленной суммы по второму варианту накопления:
![]() тыс.р.
тыс.р.
Определим величину накопленной суммы по второму варианту накопления с измененной процентной ставкой до 9%:
![]() тыс.р.
тыс.р.
Если в году m интервалов начисления, то в каждом из них процентная ставка равна j/m. Тогда наращенная сумма рассчитывается по формуле:
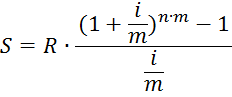
Поскольку начисление процентов производится каждые полгода, то m = 2
Рассчитаем величину накопленной суммы по первому варианту накопления:
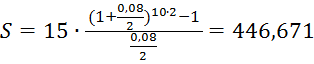 тыс.р.
тыс.р.
Наиболее предпочтителен второй вариант накопления с процентной ставкой 10%.
Задача 4
Клиент планирует разместить в банке 60 тыс.р. Сроком на два года под 10% годовых. Прогноз темпа роста инфляции составляет 8,5% в год. Определить реальную сумму денег, которую клиент сможет иметь через два года и реальную годовую ставку процента.
Решение:
Пусть Р – первоначальная сумма, n – период начисления, i – годовая процентная ставка ссудного
процента. Тогда наращенная сумма ![]() Эта сумма не учитывает инфляцию.
Эта сумма не учитывает инфляцию.
Пусть уровень инфляции за рассматриваемый период n равен
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.