







получаются либо завышенные, либо заниженные значения величины. Исключить случайные погрешности отдельных измерений невозможно, но математическая теория случайных явлений позволяет уменьшить влияние этих погрешностей на окончательный результат измерений.
Если случайная погрешность, полученная из данных измерений, окажется значительно меньше погрешности прибора, то следует оценивать результат приборной погрешностью.
Если же случайная погрешность больше приборной, то измерения следует произвести несколько раз, чтобы уменьшить значение погрешности для данной серии измерений. Чем меньшее значение погрешности мы хотим получить, тем больше измерений нужно произвести.
Результаты прямых и косвенных измерений оцениваются абсолютными и относительными погрешностями. Абсолютная погрешность Δа величины а оценивает доверительный интервал, в который попадает истинное значение измеряемой величины. Абсолютная погрешность не определяет точности измерений. Например, длину карандаша измерили сантиметровой линейкой и подучили, что длина раина l = 18,0 ± 0,5 cм. Затем этой же линейкой измерили диаметр карандаша D = 0,5 ± 0,5 см. Абсолютная погрешность - одинакова и равна половине цены наименьшего деления шкалы. Но если в первом случае измерение достаточно точно, то во втором случае ошибка равна самому измеренному значению
Для оценки точности результата измерении вводится понятие относительной ошибки ε в процентах.
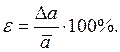
Относительной ошибкой ε
называется отношение абсолютной ошибки Δа
серии измерений к среднему арифметическому значению ![]()
За меру точности измерения принимают величину, обратную ε. Следовательно, чем меньше относительная погрешность ε, тем выше точность измерений.
2. ОСНОВЫ ТЕОРИИ СЛУЧАЙНЫХ ВЕЛИЧИН
Теория вероятностей применяется для описания совокупности большого числа (п → ∞) случайных величин, описывающих какое - либо событие. Обозначим элементы некоторой совокупности случайных величин через ai
а1, а2, ....аi....аm.....an....; n → ∞.
Все величины отличаются от некоторого среднего значения aв большую или меньшую сторону, dai= аi - а.
Вероятность появления какой - либо величины ai в интервале dai равна отношению числа значений аi, попадающих в интервал dai, к числу всех возможных значений аiпри п → ∞. Эта вероятность описывается законом нормального распределения Гаусса
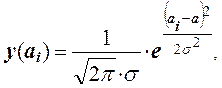
где e - основание натурального логарифма; σ2 - постоянная величина, называемая дисперсией распределения величин.
Кривая y(ai) симметрична относительно оси ОY (рис. 1)
Функция у(ai) называется плотностью распределения вероятностей.
Нормальное распределение характеризуется двумя параметрами:
1) генеральным средним значением случайной величины,
2) дисперсией генеральной совокупности.
Генеральной совокупностью называется всё множество случайных величин аi.
Генеральное среднее значение представляет собой то значение, относительно которого происходит разброс случайных величин, то есть определяется абсциссой оси симметрии кривой нормального распределения (на рис. 1. точка а).
Дисперсия σ2 характеризует быстроту уменьшения появления случайной величины аi по мере ее роста.
На рис. 1.1 приведены кривые у(ai) для трех значений σ: σ = 1, σ = 2 и σ = 4.
При малых σ кривая у(ai) идет круто и имеет большое значение уmax. Это означает, что случайные величины огромных значений встречаются реже, что большинство значений ai укладывается вблизи значения генерального
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.