Содержание
Цель работы.. 3
Расчетная схема. 3
Исходные данные. 3
Часть 1. Расчет максимального напряжения балки с бесконечным числом степеней свободы путем приведения к эквивалентной с одной степенью свободы. 4
1.1 Записываем уравнение упругой линии балки (функция статического прогиба) 4
1.2 Из условия на промежуточной опоре и граничном условии на правом конце балки определяем неизвестные параметры, входящие в уравнение упругой линии. 4
1.3 По формуле Релея определяем приближенное значение частоты собственных колебаний балки, соответствующих собственной нагрузки. 4
1.4 Определяем показатель затухания и значение собственной частоты, учитывающее демпфирование. 4
1.5 Запишем общее выражение для прогиба балки как системы с одной степенью свободы для ударного воздействия. 5
1.6 Определяем коэффициент динамичности. 5
1.7 Определяем координату точки и момента времени в которые был достигнут максимальный прогиб балки по модулю.. 5
1.8 Записываем выражение для изгибающего момента. 7
1.9 Максимальное значение изгибных напряжений. 8
Часть 2. Расчет максимального напряжения балки с бесконечным числом степеней свободы методом разложения на собственные формы балки, с использованием первых четырех форм. 9
2.1 Записываем функции Крылова: 9
2.2 Записываем общее выражение для функции формы с учетом закрепления на левом краю балки. 9
2.3 Из условия на промежуточной опоре и граничном условии на правом конце балки определяем неизвестные параметры, входящие в уравнение упругой линии. 9
2.4 Выражаем коэффициенты. 9
2.5 Подставим данные соотношения в выражение для функции формы. 9
2.6 Составляем уравнение частот. 10
2.7. Используя пакет mathematica определяем 4 наименьших положительных корня уравнения. 10
2.8 Записываем общее выражение для прогиба балки. 13
2.9 Выражение для изгибающего момента. 15
2. 10 Определяем максимальные напряжения. 16
Выводы.. 17
Цель работы: Рассчитать
максимальные напряжения в балке, возникающие в результате ударного нагружения
распределенной нагрузкой ![]() . Построить
графики прогиба балки и изгибающего момента в зависимости от координаты и
времени.
. Построить
графики прогиба балки и изгибающего момента в зависимости от координаты и
времени.
Курсовая работа состоит из 2 частей:
1. Расчет максимального напряжения методом приведения балки к системе с одной степенью свободы.
2. Расчет максимального напряжения методом разложения на собственные формы балки, с использованием первых трех форм.
Расчетная схема.
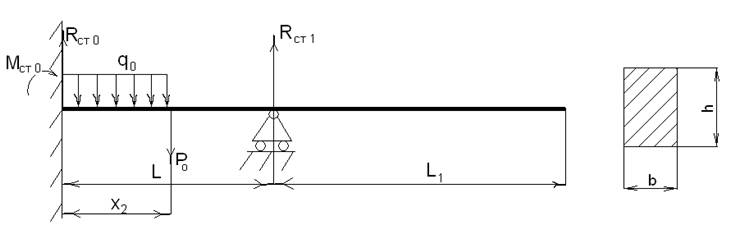 Рис.1 Расчетная
схема.
Рис.1 Расчетная
схема.
|
Воздействие на балку |
ударное. |
|
|
Нагрузка |
Р0 |
400 Н/м |
|
Распределенная нагрузка |
|
320 Н/м |
|
Длина пролетов балки |
L L1 |
2.5 м 3 м |
|
Координаты начала и конца приложения распределенной нагрузки q |
|
0 м 1.25 м |
|
Поперечное сечение балки |
b h |
15 мм 35 мм |
|
Безразмерный коэффициент демпфирования |
γ |
0.012 |
|
Модуль упругости стали |
Е |
2∙1011 Па |
|
Плотность стали |
ρ |
7800 кг/м3 |
Момент инерции балки:
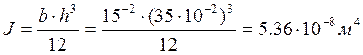
Погонная масса балки:
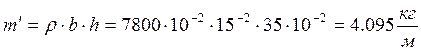
![]() =
2.5 + 3 = 5.5 м –длина балки
=
2.5 + 3 = 5.5 м –длина балки
1.1 Записываем уравнение упругой линии балки (функция статического прогиба).
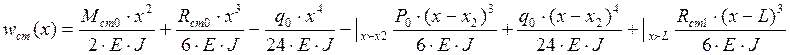
![]() ,
, ![]() -статические реакции при жесткой
заделке и на опоре
-статические реакции при жесткой
заделке и на опоре
![]() - статический момент при
жесткой заделке.
- статический момент при
жесткой заделке.
1.2 Из условия на промежуточной опоре и граничном условии на правом конце балки определяем неизвестные параметры, входящие в уравнение упругой линии.
Условие, что прогиб на опоре равен нулю.
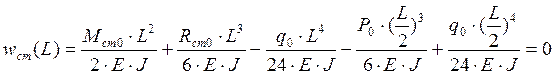
Условие, что изгибающий момент на свободном краю равен нулю.
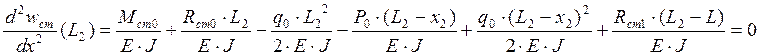
Условие, что перерезывающая сила на свободном краю равна нулю.
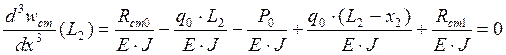
Решая систему уравнений определяем :
![]() = -328.125 Н*м
= -328.125 Н*м
![]() = 631.25 Н
= 631.25 Н
![]() = 168.75 Н
= 168.75 Н
1.3 По формуле Релея определяем приближенное значение частоты собственных колебаний балки, соответствующих собственной нагрузки.
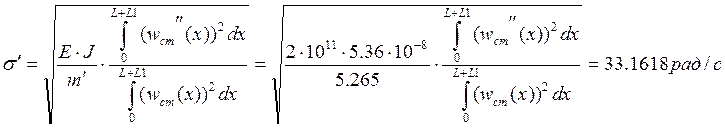
1.4 Определяем показатель затухания и значение собственной частоты, учитывающее демпфирование.
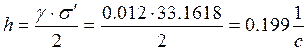
![]()
1.5 Запишем общее выражение для прогиба балки как системы с одной степенью
свободы для ударного воздействия. 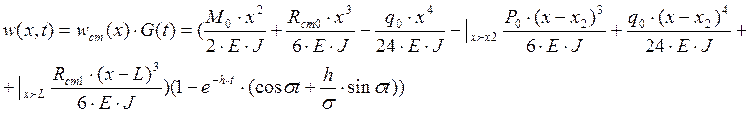
Где 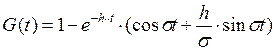
1.6 Определяем коэффициент динамичности.
![]()
1.7 Определяем координату точки и момента времени в которые был достигнут максимальный прогиб балки по модулю.
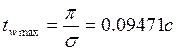
Строим график зависимости ![]()
![]()
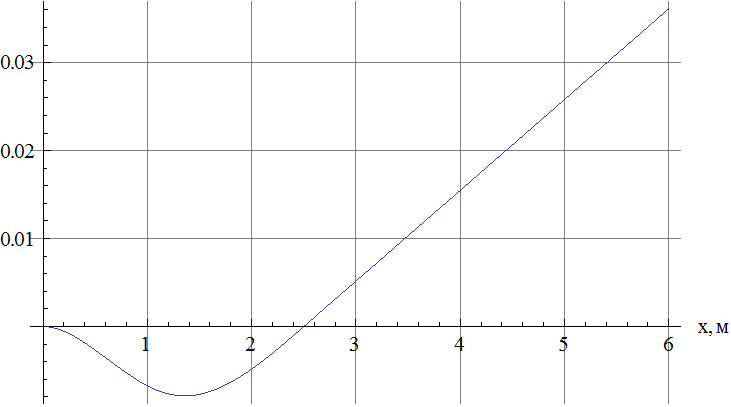
Рис.2 Изменение статического прогиба по длине балки.
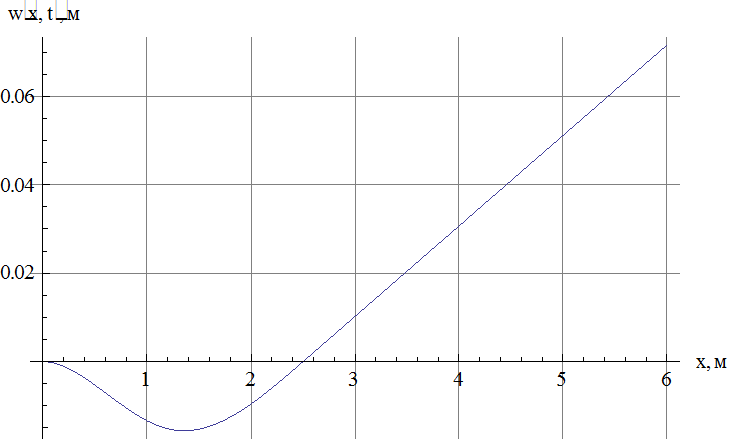
Рис.3. Зависимость прогиба от координаты в момент достижения максимального по модулю прогиба.
из рис 3 видно:
![]()
![]()
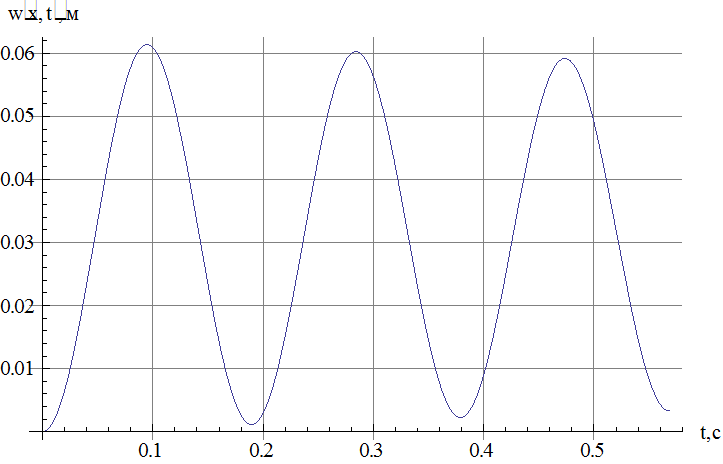
Рис.4 Зависимость прогиба от времени в сечении, в котором достигается максимальный по модулю прогиб.
1.8 Записываем выражение для изгибающего момента.
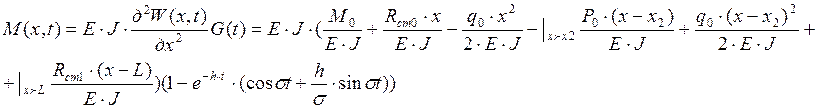 Строим
график зависимости
Строим
график зависимости ![]()
![]()
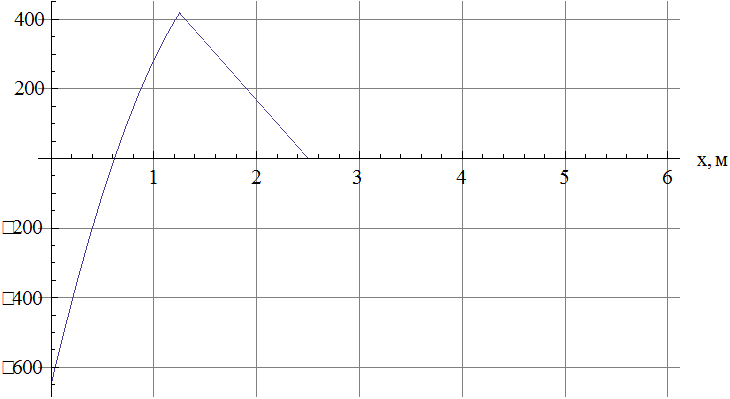
Рис.5 Зависимость изгибающего момента от координаты в момент достижения максимального по модулю изгибающего момента.
из рис 5 видно:
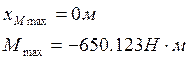
Строим график зависимости ![]() - рис.6
- рис.6
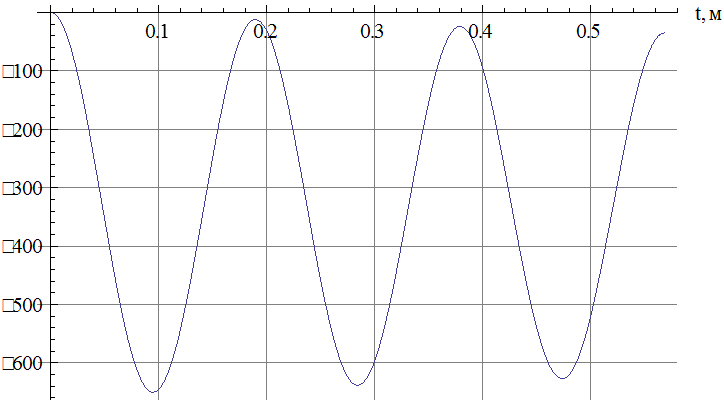
Рис.6 Зависимость изгибающего момента от времени в сечении, в котором достигается его максимальное по модулю значение
1.9 Максимальное значение изгибных напряжений.
W-момент сопротивления сечения балки
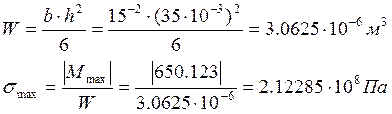
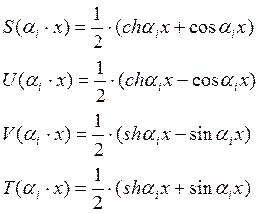
![]() -волновое
число i-ой формы
-волновое
число i-ой формы
![]()
С3i, С4i, ![]() -константы .
-константы .
i-номер формы
2.3 Из условия на промежуточной опоре и граничном условии на правом конце балки определяем неизвестные параметры, входящие в уравнение упругой линии.
Условие, что прогиб на опоре равен нулю.
![]()
Условие, что изгибающий момент на свободном краю равен нулю.
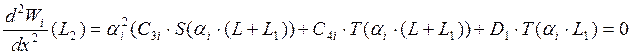
Условие, что перерезывающая сила на свободном краю равна нулю.
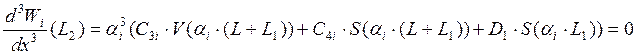
поскольку идет поиск ненулевого решения, то принимаем С3i=1
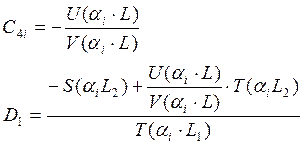
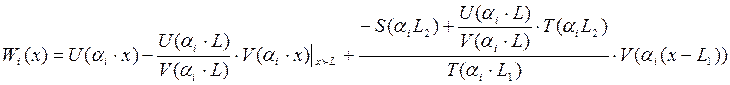
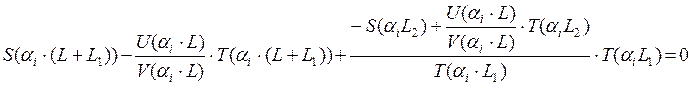
Введем 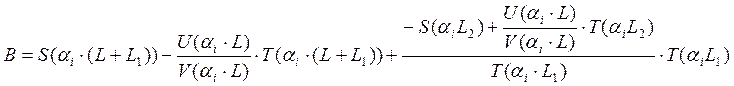
Зависимость прогиба от координаты в момент достижения максимального по модулю прогиба.
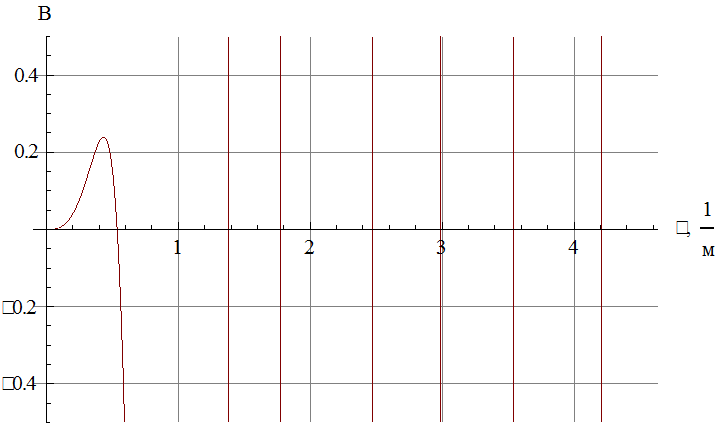
Рис. 7 График левой части уравнения.
Строим график собственных форм.
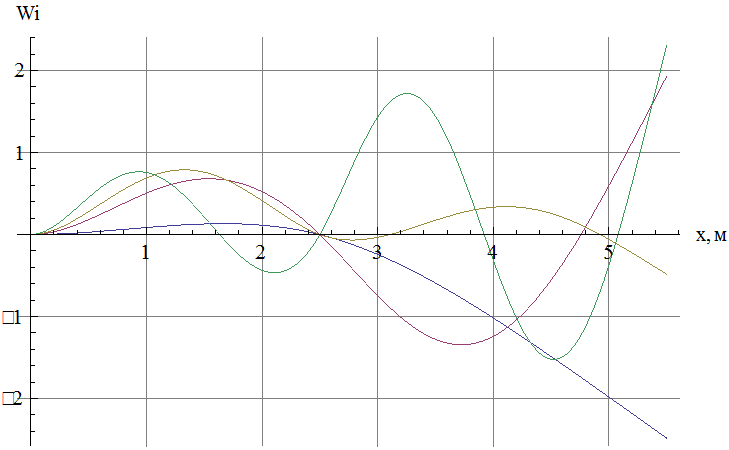 |
а) 1-я форма
Определяем коэффициенты Сi для первой формы
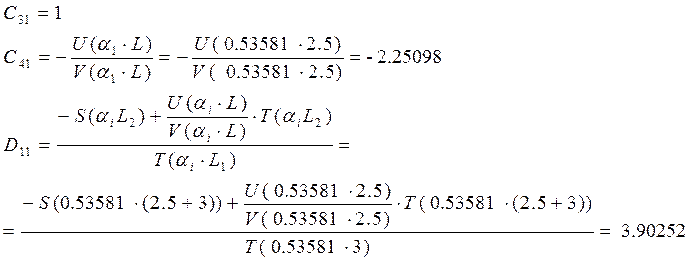
функция формы
![]()
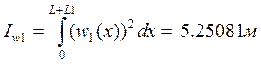
Эквивалентная масса по первой форме
![]()
Эквивалентная жесткость по первой форме
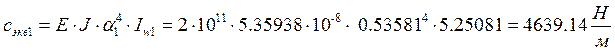
Эквивалентная сила по первой форме
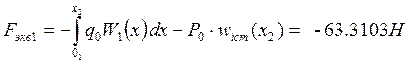
Приближенное значение первой собственной частоты
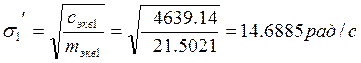
Эквивалентный коэффициент демпфирования
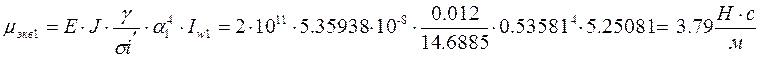
Коэффициент затухания по первой форме
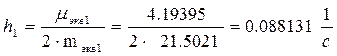
Точное значение первой собственной частоты
![]()
Временная функция
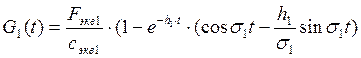
Аналогично рассчитываем для 3-х оставшихся форм и получаем следующие значения:
б) 2-я форма
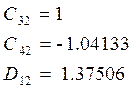
функция формы
![]()
![]()
![]()
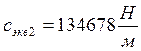
![]()
![]()
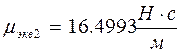
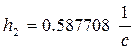
![]()
Временная функция
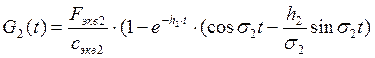
в) 3-я форма
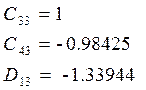
функция формы
![]()
![]()
![]()
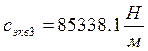
![]()
![]()
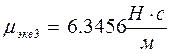
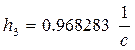
![]()
Временная функция
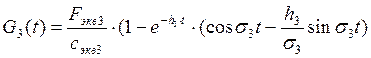
г) 4-я форма
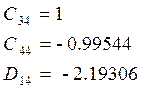
функция формы
![]()
![]()
![]()
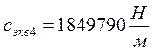
![]()
![]()
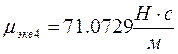
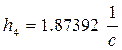
![]()
Временная функция
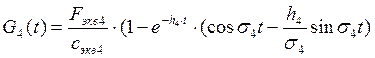
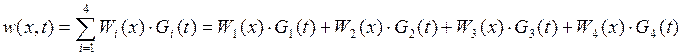
Для определения максимального по
модулю значения функции ![]() строим график.
строим график.
t, с
 x, м
x, м
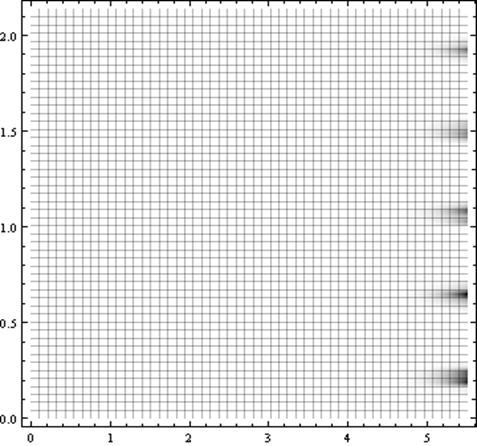
Рис.9. График функции ![]()
Из рис.9. видно, что глобальный экстремум находится в области, ограниченной следующими значениями аргумента 5 м< x<5.5 м , 0.5 с< t<0.8 с
![]()
![]()
![]()
Строим график зависимости![]() - рис.10
- рис.10 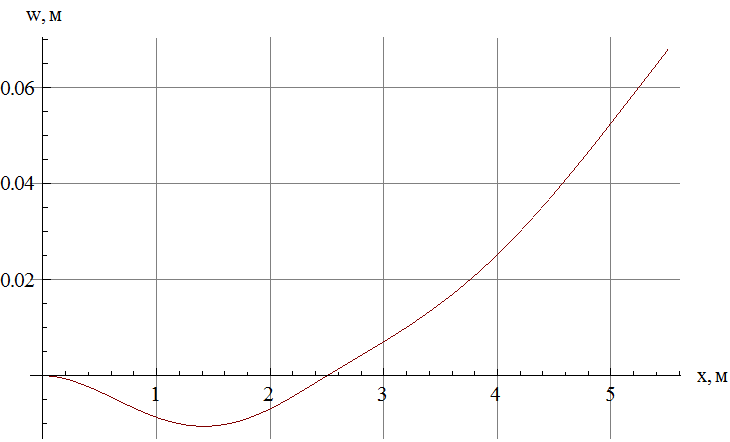
Рис.10. Зависимость прогиба от координаты в момент достижения максимального по модулю прогиба.
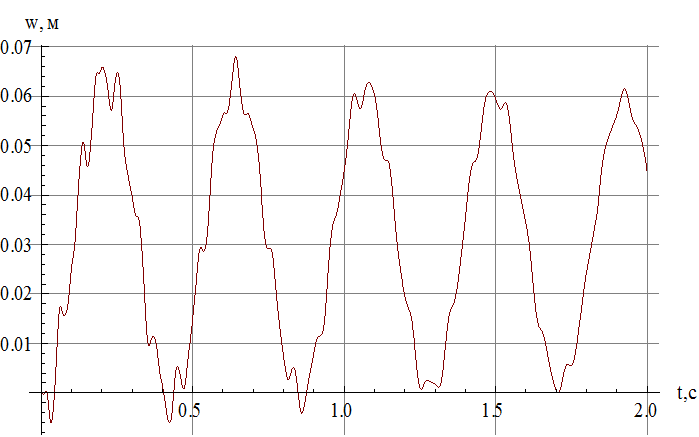
Рис.11 Зависимость прогиба от времени в сечении, в котором достигается максимальный по модулю прогиб.
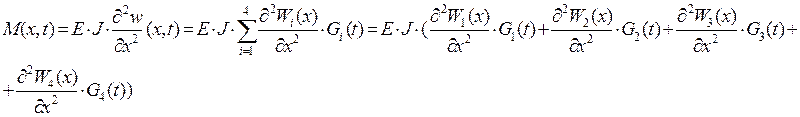
Строим график зависимости ![]() -
рис.12
-
рис.12
t, с
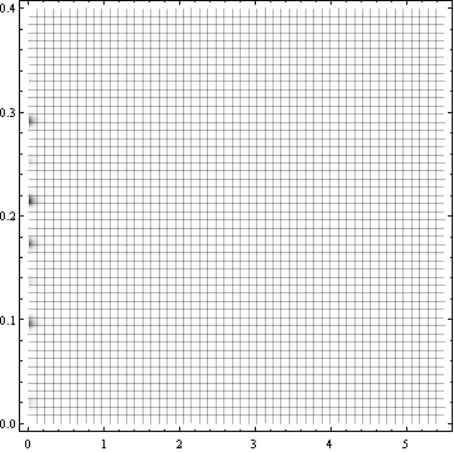 x,м
x,м
Рис. 12 График зависимости ![]()
Из рис.12 видно, что глобальный экстремум находится в области, ограниченной следующими значениями аргумента 0 м< x<0.5 м , 0 с< t<0.5 с
![]()
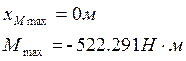
Строим график зависимости ![]()
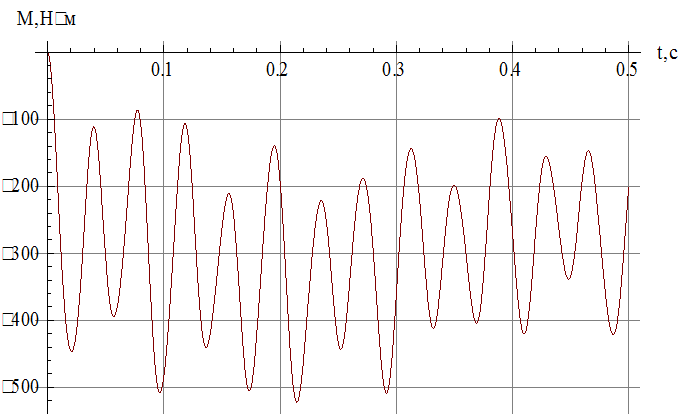
Рис.13 Зависимость изгибающего момента от времени в сечении, в котором достигается его максимальное по модулю значение
Строим график зависимости ![]() -
рис.14
-
рис.14
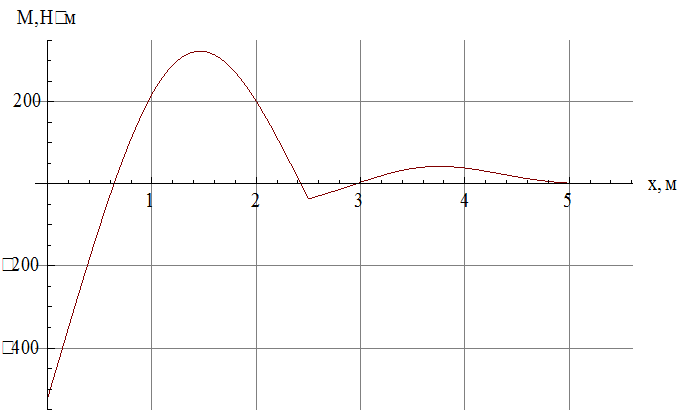
Рис.14 Зависимость изгибающего момента от координаты в момент достижения максимального по модулю изгибающего момента.

Максимальные напряжения в балке:
Из первой части: ![]()
Из второй части: ![]()
В обоих случаях напряжения меньше предела прочности стали.
Во второй части курсовой работы был получен более точный результат максимальных напряжений в балке, т.к. в первой части мы сделали грубое допущение, что балка является системой с одной степенью свободы.
Во второй части для расчета балки были использованы 4 собственных формы. Каждую форму можно рассматривать как степень свободы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.