




















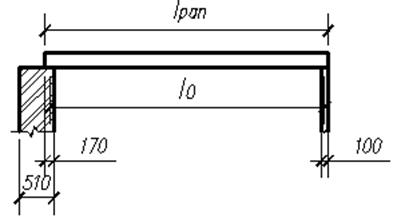
Панель (плита) рассматривается как однопролетная свободно лежащая балка, нагруженная равномерно распределенной нагрузкой по всему пролету. Расчётный пролет принимается равным расстоянию между центрами площадок опирания плиты на стены (рис. 2.4.1).
При опирании на стену расчетный пролет находим по формуле
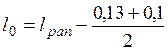 , где l0 – расчетный пролет, м;
, где l0 – расчетный пролет, м;
lpan – номинальная длина плиты, м.
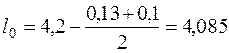 м.
м.
а)
б)
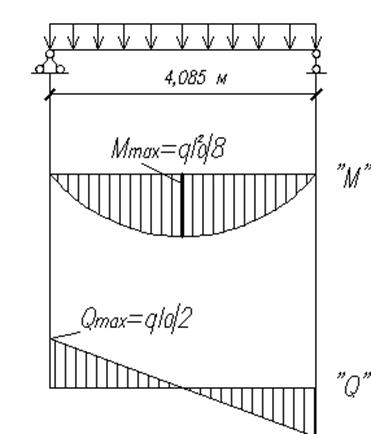
Рисунок 2.2.1 – Расчетная схема:
а – расчетный пролет; б – эпюра усилий
2.2.2 Нагрузки
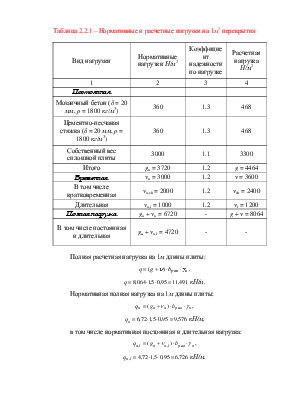
Постоянная нагрузка, действующая на плиту, складывается из нагрузки от веса пола и нагрузки от собственного веса плиты. Нормативные значения нагрузки от веса отдельных элементов пола на 1 м2 площади плиты определяются как произведение толщины слоя материала на объёмный вес этого материала. Нормативные значения временных нагрузок указываются в задании на проектирование: полная νn и её кратковременная часть νn,sh. Подсчёт значений нагрузок на 1 м2 перекрытия приведён в табл. 2.2.1.
Ширину плиты bpan = 1,5 м и коэффициент надежности по назначению здания gn = 0,95.
Таблица 2.2.1 – Нормативные и расчетные нагрузки на 1м2 перекрытия
|
Вид нагрузки |
Нормативные нагрузки Н/м2 |
Коэффициент надежности по нагрузке |
Расчетная нагрузка Н/м2 |
|
1 |
2 |
3 |
4 |
|
Постоянная |
|||
|
Мозаичный бетон (δ = 20 мм, ρ = 1800 кг/м3) |
360 |
1.3 |
468 |
|
Цементно-песчаная стяжка (δ = 20 мм, ρ = 1800 кг/м3) |
360 |
1.3 |
468 |
|
Собственный вес сплошной плиты |
3000 |
1.1 |
3300 |
|
Итого |
gn = 3720 |
1.2 |
g = 4464 |
|
Временная |
νn = 3000 |
1.2 |
ν = 3600 |
|
В том числе кратковременная |
νn,sh = 2000 |
1.2 |
νsh = 2400 |
|
Длительная |
νn,l = 1000 |
1.2 |
νl = 1200 |
|
Полная нагрузка |
gn + νn = 6720 |
- |
g + ν = 8064 |
|
В том числе постоянная и длительная |
gn + νn,l = 4720 |
- |
- |
Полная расчетная нагрузка на 1м длины плиты:
![]() ,
,
![]() кН/м.
кН/м.
Нормативная полная нагрузка на 1м длины плиты:
![]() ,
,
![]() кН/м,
кН/м,
в том числе нормативная постоянная и длительная нагрузка:
![]() ,
,
![]() кН/м.
кН/м.
2.2.3 Усилия от расчетных и нормативных нагрузок
Расчетная схема панели показана на рисунке 2.21. Для такой балки наибольший изгибающий
момент в середине пролета равен ![]() , а наибольшая поперечная сила на
опоре равна
, а наибольшая поперечная сила на
опоре равна 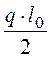 . Тогда
усилия:
. Тогда
усилия:
– от расчетной полной нагрузки
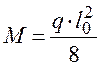 ,
,
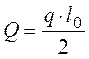 , где М – момент от расчетной
нагрузки, кН·м;
, где М – момент от расчетной
нагрузки, кН·м;
Q – поперечная сила от расчетной нагрузки, кН·м;
q – расчетная полная нагрузка, кН/м;
l0 – расчетный пролет, м.
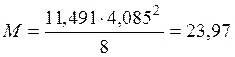 кН·м,
кН·м,
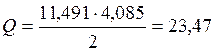 кН;
кН;
– от нормативной полной нагрузки
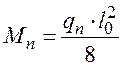 ,
,
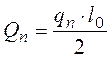 , где Мn – момент от нормативной полной
нагрузки, кН·м;
, где Мn – момент от нормативной полной
нагрузки, кН·м;
Qn – поперечная сила от нормативной полной нагрузки, кН·м;
qn – нормативная полная нагрузка, кН/м;
l0 – расчетный пролет, м.
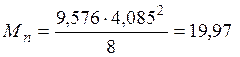 кН·м,
кН·м,
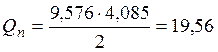 кН;
кН;
– от нормативной постоянной и длительной нагрузки
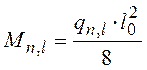 ,
,
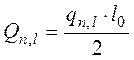 , где Мn,l – момент от нормативной постоянной и
длительной нагрузки, кН·м;
, где Мn,l – момент от нормативной постоянной и
длительной нагрузки, кН·м;
Qn,l – поперечная сила от нормативной постоянной и длительной нагрузки, кН·м;
qn,l – нормативная постоянная и длительная нагрузка, кН/м;
l0 – расчетный пролет, м.
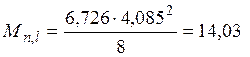 кН·м,
кН·м,
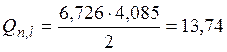 кН.
кН.
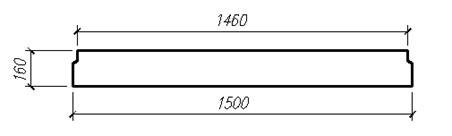
2.2.4 Компоновка поперечного сечения плиты
Принимается панель со следующими параметрами (рис 2.2.2):
– ширина панели по низу 150 - 1 = 149 см;
– ширина панели по верху,
![]() = 150 - 2×2 = 146 см;
= 150 - 2×2 = 146 см;
– принимаем высоту сечения сплошной плиты h = 16 см.
– толщина защитного слоя
бетона для рабочей арматуры – ![]() см;
см;
– рабочая высота сечения ![]() см.
см.
а)
б)
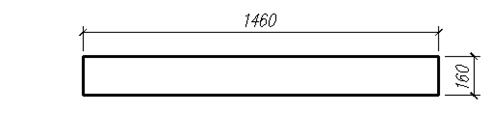
Рисунок 2.2.2. Компоновка поперечного сечения пустотной
плиты перекрытия:
а – поперечное сечение; б – приведенное сечение
2.2.5 Материал для панели
Сплошная панель перекрытия проектируется без предварительного напряжения.
В качестве ненапрягаемой арматуры плиты будем использовать стержневую арматуру класса A-III и обыкновенную арматурную проволоку периодического профиля класса Bp-I.
Характеристики арматуры класса А-III:
– нормативное сопротивление Rsn = 390 МПа;
– расчетное сопротивление Rs = 355 МПа;
– модуль упругости Es = 2,0×105 МПа.
Класс бетона для изготовления плиты В-30:
– нормативная призменная прочность Rbn=Rb,ser=22 МПа;
– расчетная призменная прочность Rb=17 МПа;
– нормативное сопротивление при растяжении Rbtn=Rbt,ser=1,8 МПа;
– расчетное сопротивление при растяжении Rbt=1,2 МПа;
– коэффициент условий работы бетона gb2=0,9;
– начальный модуль упругости бетонаEb=2,9×104 МПа;
Вычислим граничную относительную высоту сжатой зоны по формуле:
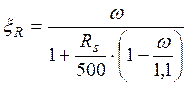 , где ξR – относительная высота
сжатой зоны;
, где ξR – относительная высота
сжатой зоны;
ω –
характеристика сжатой зоны бетона, равная ![]() ;
; ![]() ;
;
Rs – расчетное сопротивление арматуры, МПа.
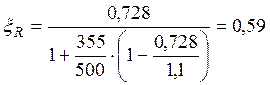
2.2.6 Расчет сплошной плиты по предельным состояниям первой группы.
2.2.6.1 Расчет прочности плиты по сечению, нормальному к
продольной оси.
Расчет прочности плиты выполняем как балки прямоугольного сечения при максимальном изгибающем моменте в середине пролета М = 23,97 кН×м.
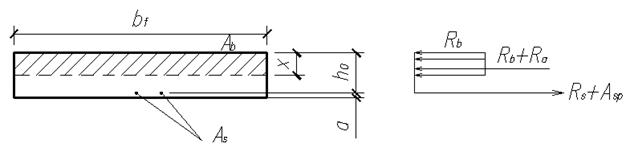
Рисунок 2.2.3 – К расчету прочности нормальных сечений
изгибаемых элементов
Для определения площади арматуры Аsp вначале вычисляем αm, затем по таблице принимаются ξ и ζ, и из условия равновесия по ζ находим Аsp.
Вычисляем
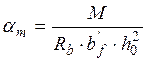 , где М – момент от расчетной
нагрузки, кН·м;
, где М – момент от расчетной
нагрузки, кН·м;
Rb – расчетная призменная прочность бетона, МПа;
![]() – ширина панели по верху, см;
– ширина панели по верху, см;
h0 – рабочая высота сечения пустотной плиты, см.
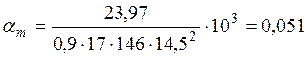 , где 103 – множитель для
приведения числителя и знаменателя к одним единицам.
, где 103 – множитель для
приведения числителя и знаменателя к одним единицам.
По значению am находим x = 0,053 < xR = 0,59 и z = 0,974. Так как ![]() см < 0,5 · h = 8 см, то нейтральная ось
сечения проходит в пределах полки и площадь сечения растянутой арматуры
вычисляем по формуле:
см < 0,5 · h = 8 см, то нейтральная ось
сечения проходит в пределах полки и площадь сечения растянутой арматуры
вычисляем по формуле:
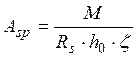 , где Аsp –площадь арматуры, см2;
, где Аsp –площадь арматуры, см2;
М – момент от расчетной нагрузки, кН·м;
Rs – расчетное сопротивление арматуры, МПа;
h0 – рабочая высота сечения пустотной плиты, см;
Определим Asp:
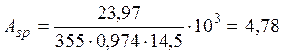 см.
см.
По сортаменту принимаем
10 Æ 8 А-III с площадью Asp = 5,03 см2, что
превышает требуемую расчетную площадь на 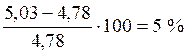 .
.

Рисунок 2.2.4 – Армирование пустотной плиты
2.2.7 Расчет сплошной плиты по предельным состояниям второй группы.
2.2.7.1 Определение геометрических характеристик приведенного сечения.
Приведенное сечение включает в себя сечение бетона, а также сечение продольной арматуры, умноженное на отношение модулей упругости арматуры и бетона.
Отношение модулей упругости:
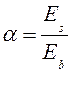 , где α – отношение модулей
упругости;
, где α – отношение модулей
упругости;
Еs – модуль упругости арматуры, МПа;
Еb – начальный модуль упругости бетона, МПа.
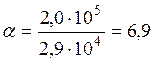
Площадь приведенного сечения:
![]() , где Аred – площадь приведенного сечения, см2
(рисунок 2.2.5);
, где Аred – площадь приведенного сечения, см2
(рисунок 2.2.5);
![]() –
ширина панели по верху, см;
–
ширина панели по верху, см;
h – высота сечения сплошной плиты, см.
![]() см2.
см2.
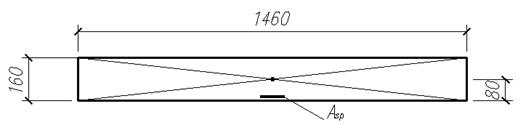
Рисунок 2.2.5 – К определению геометрических характеристик приведенного сечения
Расстояние от нижней грани до центра тяжести приведенного сечения:
![]() , где
у0 – расстояние от нижней грани до центра тяжести
приведенного
, где
у0 – расстояние от нижней грани до центра тяжести
приведенного
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.