Сбор нагрузок на фундамент. Расчет конструкции по первой и второй группам предельных состояний, страница 3

b – ширина подошвы фундамента, м;

р_max– максимальное давление под подошвой фундамента, кПа;

p_i – напряжения в любом расчетном сечении подошвы фундамента, кПа;

l_i – расстояние от оси фундамента до рассматриваемого сечения, м;

l – длина фундамента, м, ( l= 1 м, т.к. фундамент ленточный).

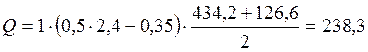 кН.

Проверим выполнение условия

, где Q_I– поперечная сила в сечении I – I, кН;

 φ_b3 – коэффициент, принимаемый для тяжелого и ячеистого бетонов, равным 0,6;

R_bt – расчетное сопротивление бетона растяжению, МПа, (R_bt = 1,05 МПа);

l – длина фундамента, м,

h₀ – рабочая высота сечения, м.

.

Условие выполняется.

Средний периметр пирамиды продавливания и расчетную продавливающую силу определим по формулам

;

, где u_m – средний периметр пирамиды продавливания, м;

l_к, l_н– длина фундамента, м (l_к = l_н = 1 м);

F– расчетная продавливающая сила, кН;

–  среднее напряжение под подошвой фундамента от расчетных нагрузок, кПа;

 – площадь подошвы фундамента, м².

 м;

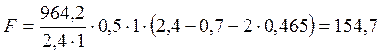 кН.

Проверим выполнение условия

, где F– расчетная продавливающая сила, кН;

φ_b – коэффициент, принимаемый равным 1 для тяжелых бетонов;

R_bt – расчетное сопротивление бетона растяжению, МПа;

u_m – средний периметр пирамиды продавливания, м.

.

Условие выполняется, следовательно, прочность фундамента на продавливание обеспечена.

Найдем изгибающий момент в сечении у грани стены по формуле

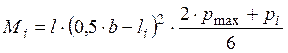, где М – изгибающий момент в сечении у грани стены, кН·м;

b – ширина подошвы фундамента, м;

р_max– максимальное давление под подошвой фундамента, кПа;

p_i – напряжения в любом расчетном сечении подошвы фундамента, кПа;

l_i – расстояние от оси фундамента до рассматриваемого сечения, м;

l – длина фундамента, м.

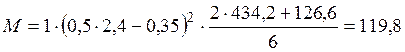 кН·м.

В качестве рабочих стержней примем арматуру класса А-II с расчетным сопротивлением R_s= 280 МПа.

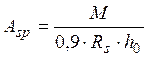, где  А_sp –площадь арматуры, см²;

М – момент от расчетной нагрузки, кН·м;

R_s – расчетное сопротивление арматуры, МПа;

h₀ – рабочая высота сечения плиты, м.

.

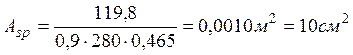По сортаменту принимаем 5 Æ 16 А-II с площадью A_sp = 10,05 см². Шаг стержней s = 200 мм. Площадь распределенной арматуры   см². Так как в ленточном фундаменте совместно работают две консольные части сечения фундамента, то требуемое количество распределительной арматуры следует увеличить вдвое, т.е.  см². Тогда принимаем 4 Æ 8 А-I с площадью A_sp = 2,01 см².  Шаг стержней s = 300 мм.   

Напряжения в грунте под подошвой фундамента у грани стены от нормальных нагрузок определим по формуле

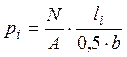, где р – напряжения в грунте под подошвой фундамента у грани стены от нормальных нагрузок, кПа;

N – суммарная вертикальная сила от расчетных нагрузок на уровне подошвы фундамента, кН;

М – суммарный момент от расчетных нагрузок на уровне подошвы фундамента, кН·м;

W – момент сопротивления подошвы фундамента, м³;

l_i – расстояние от оси фундамента до рассматриваемого сечения, м;

b – ширина фундамента, м.

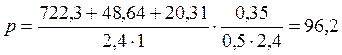 кПа.

Изгибающий момент  у грани стены от нормальных нагрузок

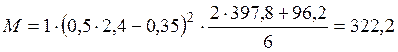 кН·м.

Модуль упругости арматуры  E_s = 210000 МПа, начальный модуль упругости бетона E_b=27000 МПа. Определим соотношение .

Коэффициент армирования сечения:

    , где μ – коэффициент армирования сечения;

А_s –площадь арматуры, см²;

h– высота плиты, см.

.

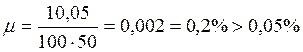Упругопластический момент сопротивления сечения фундамента определим по формуле

,

где W_pl– упругопластический момент сопротивления сечения фундамента,м³;

γ₁ = 0, так как сечение прямоугольное;

μ – коэффициент армирования сечения;

n – соотношение между модулями упругости арматуры и бетона;

l – длина фундамента, м;

h– высота плиты, см.

 м³.