
где Qi – вероятность данной гипотезы после испытания;
Pi – вероятность этой же гипотезы до испытания;
pi -условная вероятность события, появляющегося при испытаниях по этой гипотезе;
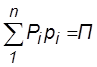 - полная вероятность события, появляющегося при испытании;
- полная вероятность события, появляющегося при испытании;
n – число гипотез.
В том случае, когда до испытания гипотезы равновероятны, т. е. P1 = P2 = P3 = ...= Pn = P, то вероятность гипотезы после испытания равна условной вероятности события по этой гипотезе, деленной на сумму таких вероятностей по всем гипотезам, т. е.
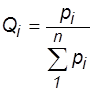 .
.
Теорема гипотез широко используется в теории стрельбы, в частности, с ее помощью может быть рассчитан новый закон распределения случайной величины (например, центра рассеивания снарядов относительно цели) после испытания.
Некоторые числовые характеристики случайных величин (СВ)
Среднее арифметическое значение (СВ)
Среднее арифметическое значение СВ (хср) равно сумме парных произведений частных значений этой величины на соответствующие им частоты:
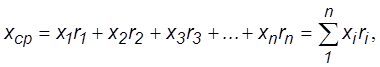
где х1, х2, х3, ... – частные значения СВ;
r1, r2, r3, ... – частоты, соответствующие этим частным значениям.
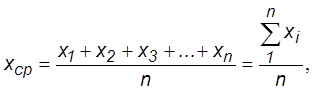
где х1, х2, х3, ... – частные значения СВ, полученные при ее испытании;
n – число частных значений СВ;
хср – имеет размерность самой случайной величины.
Для того чтобы определить математическое ожидание СВ, необходимо знать закон распределения СВ – зависимость между возможными значениями СВ и соответствующими им вероятностями, которая в частном случае может быть выражена, например, таблицей в следующем виде:
|
xi |
x1 |
x2 |
x3 |
... |
xn |
|
|
pi |
p1 |
p2 |
p3 |
... |
pn |
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.