Моделирование температурных и концентрационных зависимостей параметров кремния

Моделирование температурных и концентрационных зависимостей параметров кремния.

1. Моделирование удельного сопротивления кремния от концентрации легирующей примеси и температуры.

Рассматривается однородно легированный полупроводник, имеющий концентрацию доноров  и концентрацию акцепторов , которые определяются из решения уравнения:

q – заряд;

p – концентрация дырок;

n– концентрация электронов;

 – концентрация ионов доноров;

 – концентрация ионов акцепторов.

Параметры данного уравнения являются функциями зависящими от уровня ферми и температуры:

; где F_1/2 – интеграл Ферми:

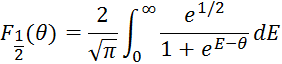
В общем случае концентрация ионов примеси зависит от уровня Ферми и температуры:

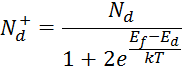
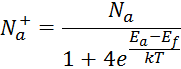
В рассматриваемом диапазоне температур: 200…400 K считается что вся примесь ионизирована.

Удельное сопротивления полупроводника:

 p – тип проводимости;

 n – тип проводимости.

Как видно из данных формул температурно-концентрационная зависимость удельного сопротивления полупроводника(кремния) определяется температурно-концентрационной зависимостью подвижности, данная зависимость наилучшим образом отражена в модели Зильбергера.

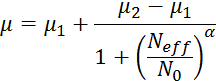
В зависимости от типа проводимости коэффициенты , ,  определяются:

1.  n-тип

2.  p-тип                                                

Коэффициенты  общий как для n, так и для p типа проводимости.

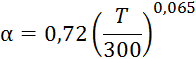
Расчет данных зависимостей осуществлялся с помощью модуля ro_si.cpp:

1). Ro – функция расчета удельного сопротивления.

2). SplineRoN – сплайн-модель удельного сопротивления n-Si

3). SplineRoP – сплайн-модель удельного сопротивления p-Si

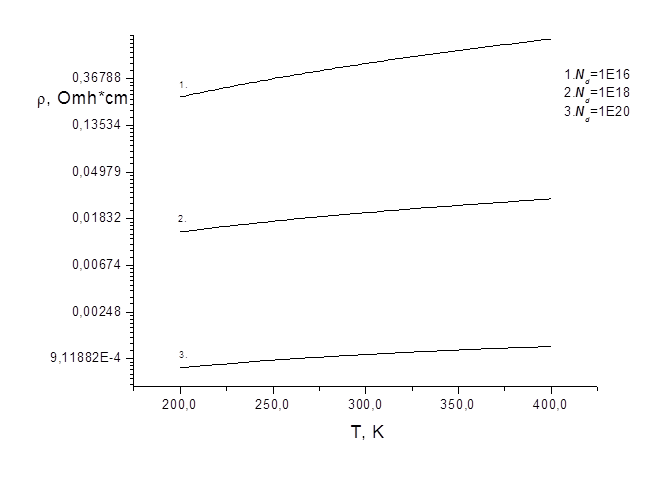
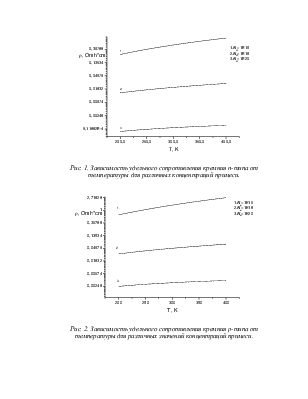
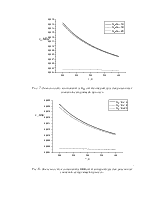
Рис. 1. Зависимость удельного сопротивления кремния n-типа от температуры для различных концентраций примеси.

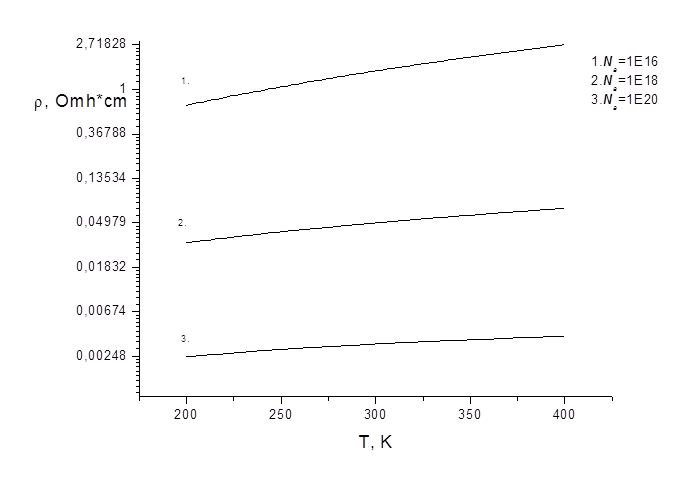
Рис. 2. Зависимость удельного сопротивления кремния p-типа от температуры для различных значений концентраций примеси.

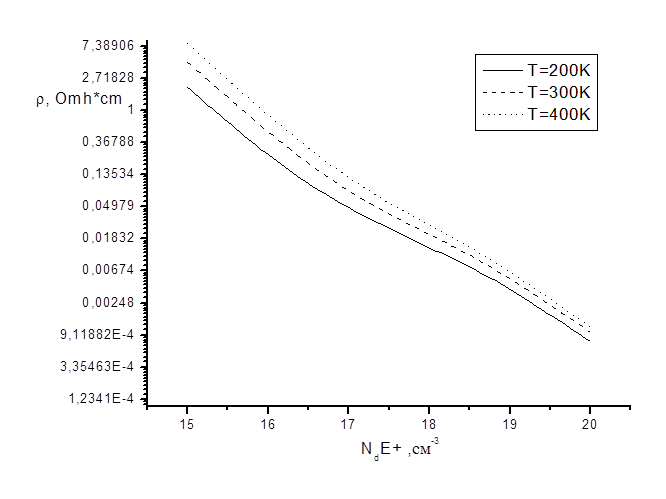
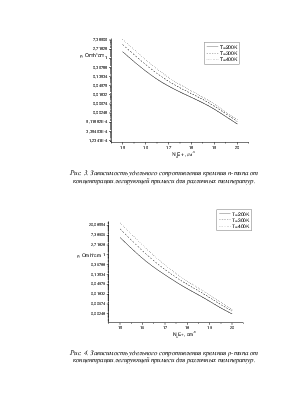
Рис. 3. Зависимость удельного сопротивления кремния n-типа от концентрации легирующей примеси для различных температур.

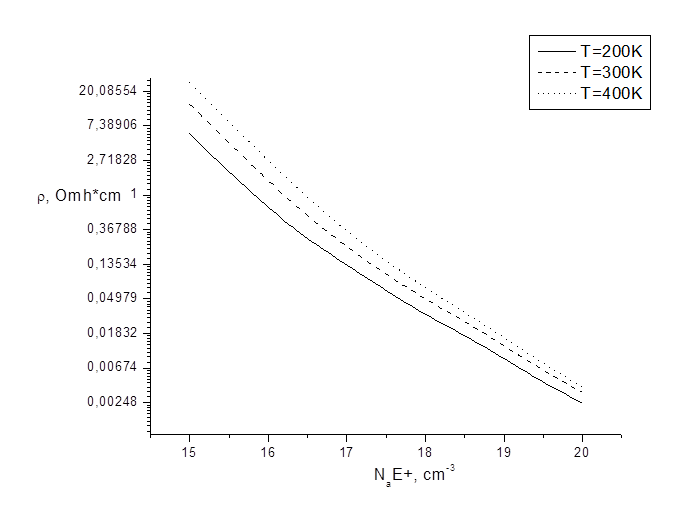
Рис. 4. Зависимость удельного сопротивления кремния p-типа от концентрации легирующей примеси для различных температур.

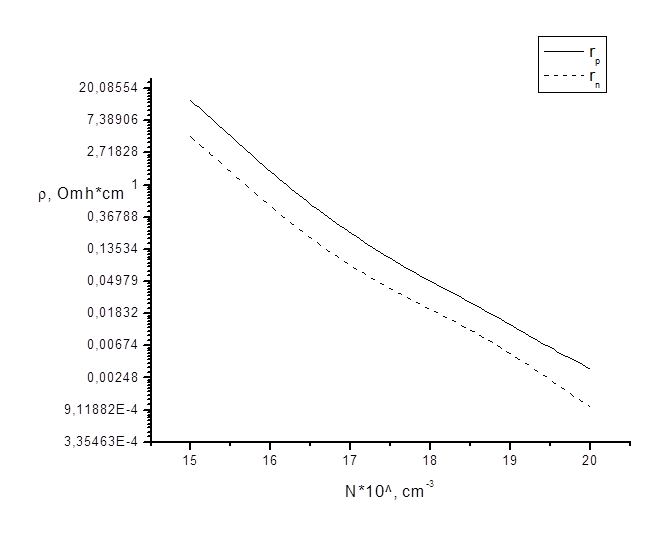
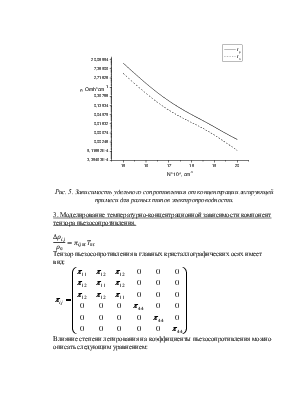
Рис. 5. Зависимость удельного сопротивления от концентрации легирующей примеси для разных типов электропроводности.

3. Моделирование температурно-концентрационной зависимости компонент тензора пьезосопротивления.

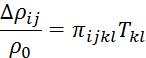
Тензор пьезосопротивления в главных кристаллографических осях имеет вид:

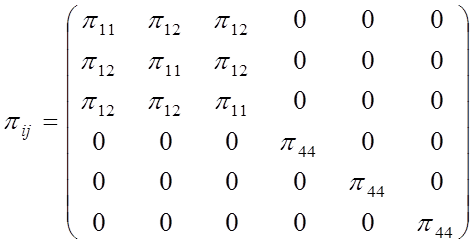
Влияние степени легирования на коэффициенты пьезосопротивления можно описать следующим уравнением:

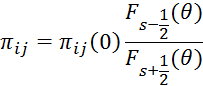
 – компонента тензора пьезосопротивления для слаболегированного полупроводника.

Для получения графических зависимостей компонент тензора пьезосопротивления использовался модуль pi_si.cpp:

1). PIn – расчет пьезорезистивных коэффициентов для n-Si

2). PIp – расчет пьезорезистивных коэффициентов для p-SI

3). SplinePFn – cплайн -модель Pi-фактора для кремния n-типа

4). SplinePFp – cплайн-модель Pi-фактора для кремния p-типа

5). PItoL – расчет пьезорезистивного коэффициента для кремния в заданном направлении

6). TenzorPIq – формирование тензора пьезосопротивления в в кристаллографической системе координат

7). TenzorPIx – формирование тензора пьезосопротивления в в произвольной системе

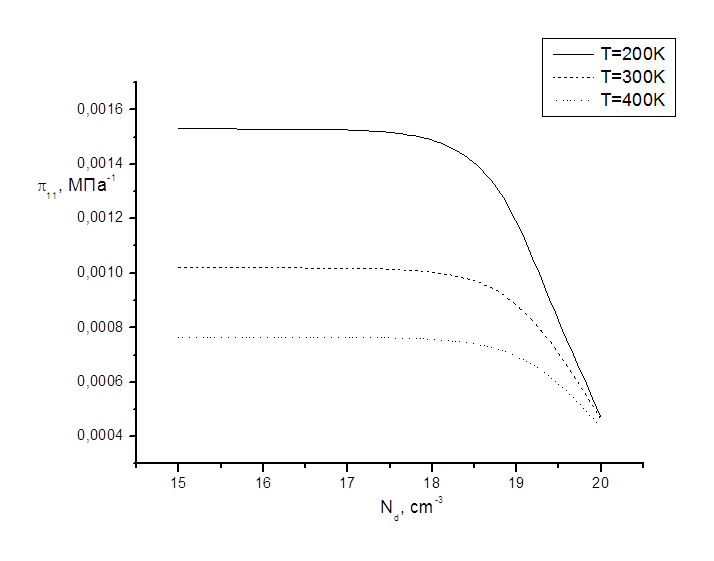
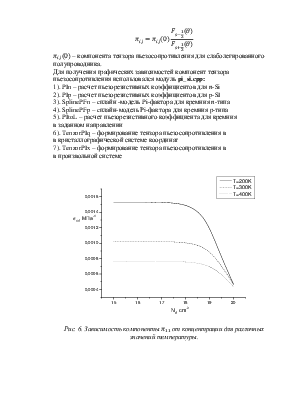
Рис. 6. Зависимость компонентыот концентрации для различных значений температуры.

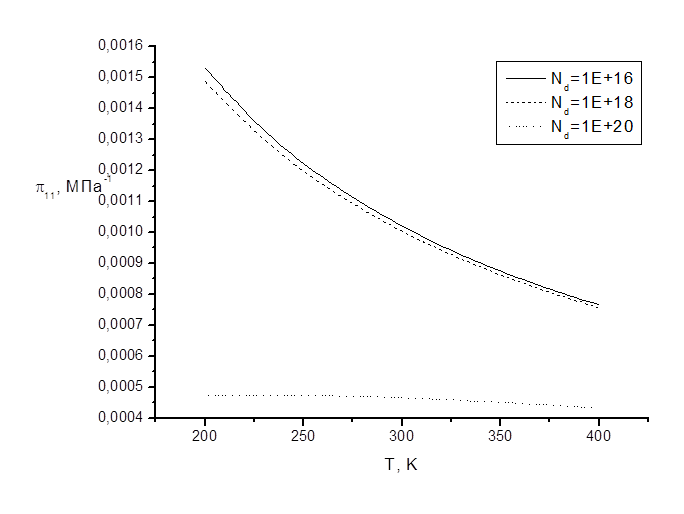
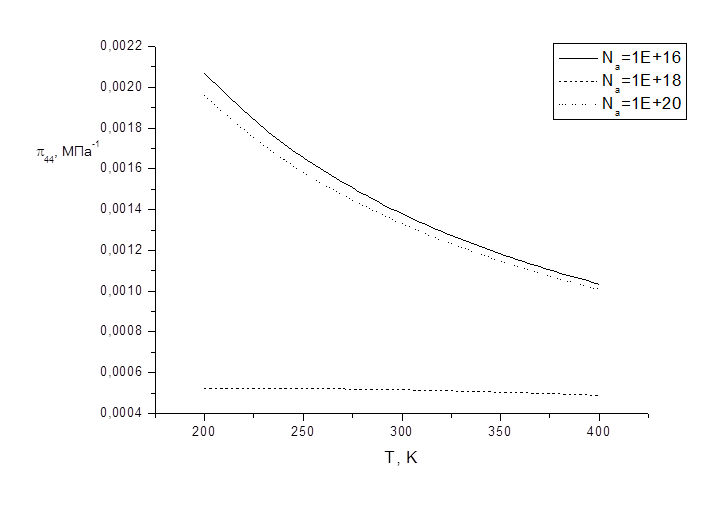
Рис. 7. Зависимость компонентыот температуры для различных значений легирующей примеси

.

Рис. 8. Зависимость компоненты  от температуры для различных значений легирующей примеси.

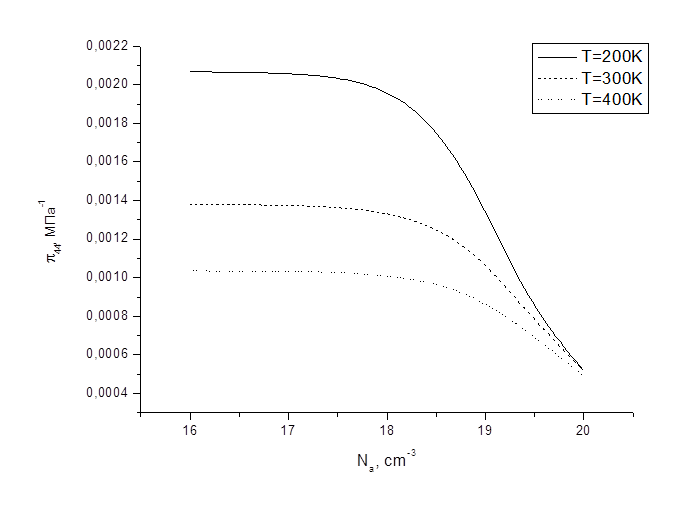
Рис. 9. Зависимость компоненты  от концентрации легирующей примеси для различных значений температуры.