





Построение Spline моделей.
1D-Spline(теоретическая часть).
При большом количестве узлов интерполяции сильно возрастает степень интерполяционных многочленов, что делает их неудобными для проведения вычислений. Высокой степени многочленов можно избежать, разбив отрезок интерполирования на несколько частей, с построением в каждой части своего интерполяционного полинома. Такой метод называется интерполяцией сплайнами. Наиболее распространенным является построение на каждом отрезке [xi, xi+1], i=0..n-1 кубической функции.
Сплайн – это кусочно полиномиальная функция. Кубический сплайн на каждом из частичных отрезков [xi, xi+1] будет иметь вид:
![]()
где
![]() и
и ![]() неизвестные
коэффециенты, выбирающиеся таким образом, чтобы интерполирующие сплайны имели
одинаковые производные первого и второго порядка в точках сшивки.
неизвестные
коэффециенты, выбирающиеся таким образом, чтобы интерполирующие сплайны имели
одинаковые производные первого и второго порядка в точках сшивки.
Уравнения для определения коэффициентов ![]() и
и ![]() можно
получить из:
можно
получить из:
1. Условия равенства значений интерполируемой функции и сплайна в узловых точках
![]()
2. Сшивки на границах элементарных интервалов первых производных сплайнов
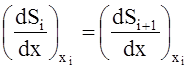 , (i = 1,2, …, n-1)
, (i = 1,2, …, n-1)
3. Сшивки на границах элементарных интервалов вторых производных сплайнов
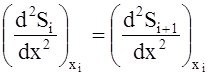 , (i = 1,2, …, n-1)
, (i = 1,2, …, n-1)
4. Условие «Свободного закрепления концов»
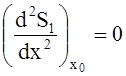 ;
; 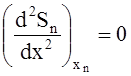 ;
;
Использование данных условий и кубического сплайна приводит к следующей системе уравнений:
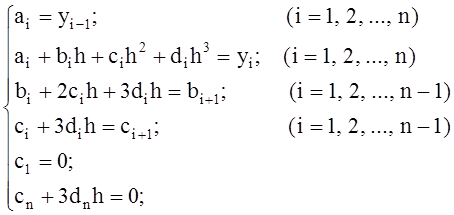
Где ![]() - расстояние между соседними точками (шаг
по x).
- расстояние между соседними точками (шаг
по x).
Алгоритм определния коэффициентов кубического сплайна:
1. Определение
коэффициентов ![]() :
:
![]() (i = 1, 2, …, n)
(i = 1, 2, …, n)
2. Формирование матрицы коэффициентов и вектора свободных членов СЛАУ
-
элементы главной диагонали ![]()
-
элементы побочных диагоналей ![]()
-
компоненты вектора свободных членов 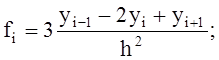
3. Решение СЛАУ относительно
![]() (i = 2, 3, …, n)
(i = 2, 3, …, n)
И
дополнение массива коэффициентов с элементом ![]()
4. Расчет
коэффициентов ![]()
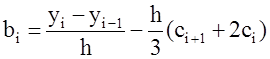 (i = 2, 3, …, n)
(i = 2, 3, …, n)
5. Расчет
коэффциентов ![]()
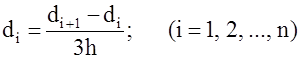
Построение одномерных сплайн моделей:
В данной работе использовалась программа Sensor modeling моделирующая зависимости выходного сигнала от температуры и давления(Рис. 1.):
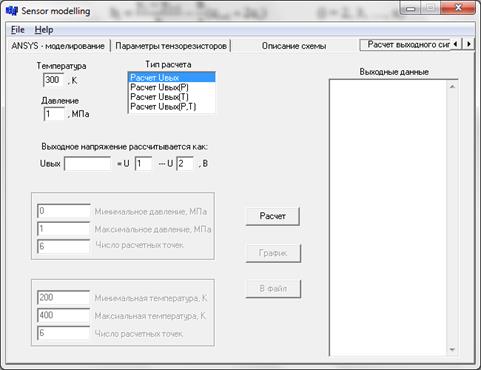
Рис. 1. Используемая программа.
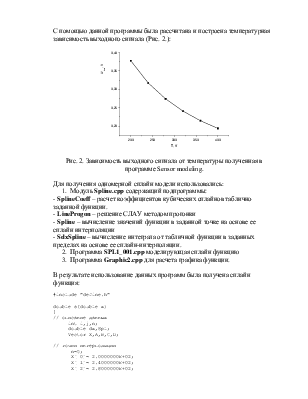
С помощью данной программы была рассчитана и построена температурная зависимость выходного сигнала (Рис. 2.):
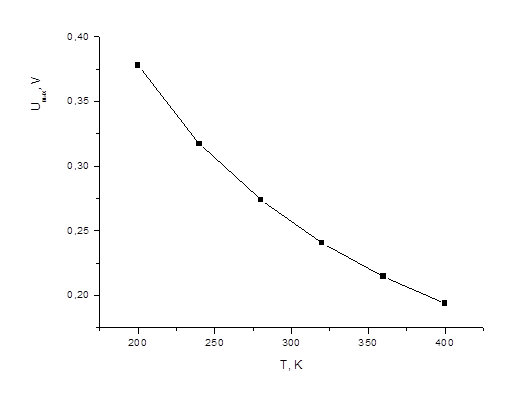
Рис. 2. Зависимость выходного сигнала от температуры полученная в программе Sensor modeling.
Для получения одномерной сплайн модели использовались:
1. Модуль Spline.cpp содержащий подпрограммы:
- SplineCoeff – расчет коэффициентов кубических сплайнов таблично заданной функции.
- LineProgon– решение СЛАУ методом прогонки
- Spline – вычисление значений функции в заданной точке на основе ее сплайн интерполяции
- SdxSpline – вычисление интеграла от табличной функции в заданных пределах на основе ее сплайн-интерполяции.
2. Программа SPL1_001.cpp моделирующая сплайн функцию
3. Программа Graphic2.cpp для расчета графика функции.
В результате использование данных программ была получена сплайн функция:
#include "define.h"
double s(double x)
{
// описание данных
int i,j,n;
double dx,Spl;
Vector X,A,B,C,D;
// точки интерполяции
n=5;
X[ 0]= 2.0000000E+02;
X[ 1]= 2.4000000E+02;
X[ 2]= 2.8000000E+02;
X[ 3]= 3.2000000E+02;
X[ 4]= 3.6000000E+02;
X[ 5]= 4.0000000E+02;
// коэфффициенты сплайнов
A[ 1]= 3.7784000E-01; B[ 1]=-1.6093600E-03;
A[ 2]= 3.1741000E-01; B[ 2]=-1.3135299E-03;
A[ 3]= 2.7400000E-01; B[ 3]=-9.2452033E-04;
A[ 4]= 2.4076000E-01; B[ 4]=-7.3713876E-04;
A[ 5]= 2.1473000E-01; B[ 5]=-5.7217464E-04;
C[ 1]= 0.0000000E+00; D[ 1]= 6.1631280E-08;
C[ 2]= 7.3957536E-06; D[ 2]=-4.2218900E-08;
C[ 3]= 2.3294856E-06; D[ 3]= 2.1306818E-10;
C[ 4]= 2.3550538E-06; D[ 4]=-4.8833732E-09;
C[ 5]= 1.7690490E-06; D[ 5]=-1.4742075E-08;
// определение номера интервала, в который попадает x
j=0;
for (i=1; i<=n; i++)
if ((x >= X[i-1])&&(x < X[i])) j=i;
if ((x >= X[n-1])&&(x <= X[n])) j=n;
if (j==0) return 0.0;
// вычисление значения сплайна
dx=x-X[j-1];
Spl=A[j]+B[j]*dx+C[j]*dx*dx+D[j]*dx*dx*dx;
// завершение
return Spl;
}
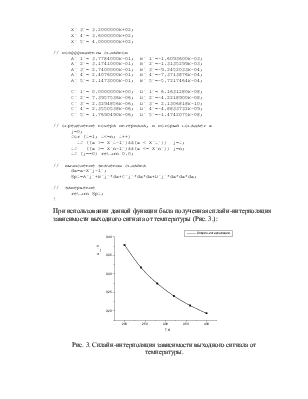
При использовании данной функции была полученная сплайн-интерполяция зависимости выходного сигнала от температуры (Рис. 3.):
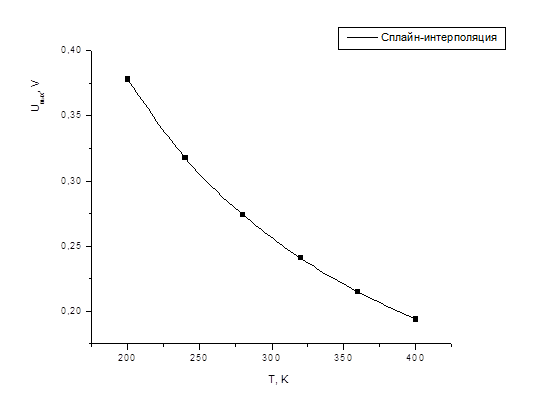
Рис. 3. Сплайн-интерполяция зависимости выходного сигнала от температуры.
2D-Spline(теоретическая часть).
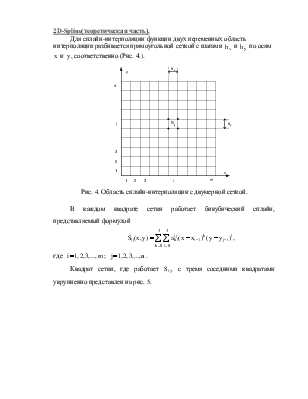
Для сплайн-интерполяции функции двух
переменных область интерполяции разбивается прямоугольной сеткой с шагами ![]() и
и ![]() по осям
по осям
![]() и
и ![]() ,
соответственно (Рис. 4.).
,
соответственно (Рис. 4.).
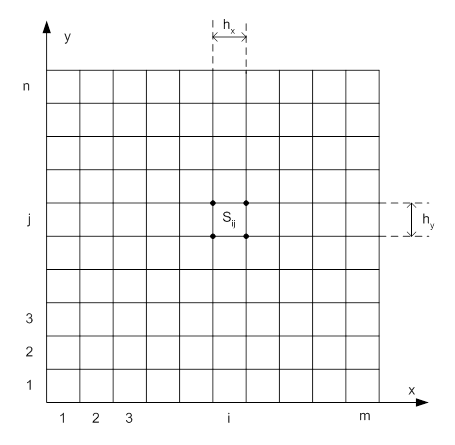
Рис. 4. Область сплайн-интерполяции с двумерной сеткой.
В каждом квадрате сетки работает бикубический сплайн, представляемый формулой
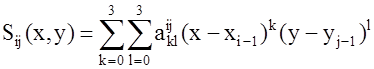 , где
, где ![]() ;
; ![]() .
.
Квадрат
сетки, где работает ![]() , с тремя соседними квадратами
укрупненно представлен на рис. 5.
, с тремя соседними квадратами
укрупненно представлен на рис. 5.
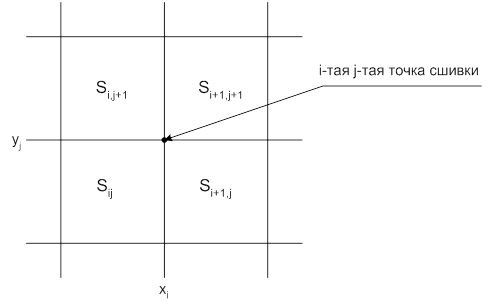
Рис. 5. Фрагмент сетки вблизи точки с индексами i и j
Коэффициенты ![]() кубического сплайна рассчитываются из
условия непрерывности сплайна
кубического сплайна рассчитываются из
условия непрерывности сплайна ![]() и его первых и вторых
производных в узлах сетки. Для i-го j-го узла они могут быть записаны следующим
образом:
и его первых и вторых
производных в узлах сетки. Для i-го j-го узла они могут быть записаны следующим
образом:
![]() ;
;
![]() ;
;
![]() ;
;
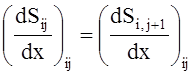 ;
;
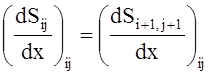 ;
;
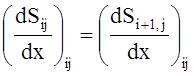 ;
;
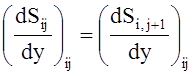 ;
;
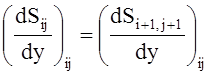 ;
;
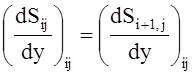 ;
;
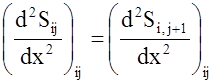 ;
;
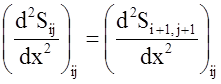 ;
;
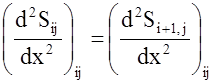 ;
;
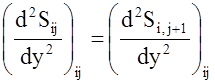 ;
;
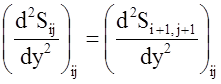 ;
;
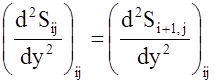 ;
;
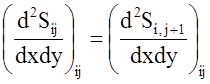 ;
;
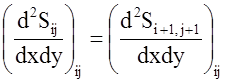 ;
;
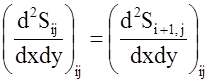 ;
; 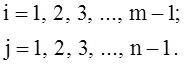
Всего – 18(m-1)(n-1) уравнений. Недостающие уравнения для определения 16mn коэффициентов сплайнов определяются из условий на границах области интерполяции.
Граничные условия:
1. в граничных узлах сетки задаются значения первых частных производных по x и по y интерполируемой функции, а в угловых узлах – значения второй смешанной производной;
2. в граничных узлах сетки задаются значения вторых частных производных по x и по y интерполируемой функции, а в угловых узлах – значения второй смешанной производной;
3.
требуют, чтобы сплайн был периодической функцией с периодом ![]() по переменной
по переменной ![]() и с
периодом
и с
периодом ![]() по переменной
по переменной ![]() ;
;
4.
требуют, чтобы на линиях ![]() ,
, ![]() ,
, ![]() ,
, ![]() были бы непрерывные производные вплоть до
пятого порядка. Сплайн, удовлетворяющий этим условиям, обладает повышенной
гладкостью.
были бы непрерывные производные вплоть до
пятого порядка. Сплайн, удовлетворяющий этим условиям, обладает повышенной
гладкостью.
Построение двумерных сплайн моделей:
Использовалась программа Sensor modeling позволяющая смоделировать зависимость выходного сигнала от температуры и давления (рис. 1.).
С помощью программы мы получили набор точек описывающий характер данной зависимости (Рис. 6.)
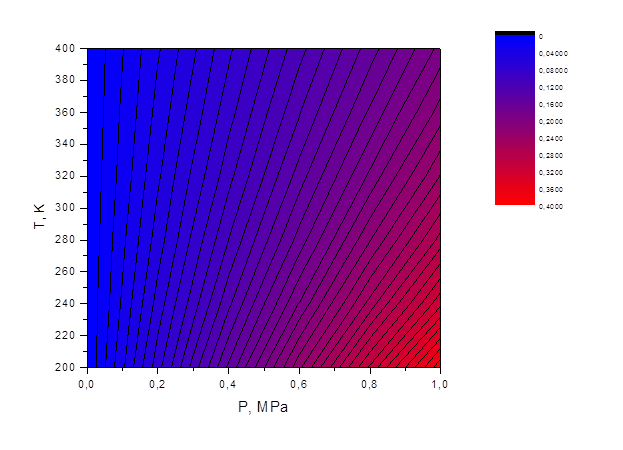
Рис. 6. Зависимость выходного сигнала от температуры и давления.
Для получения двумерной сплайн модели использовались:
1. Модуль Spline2D.cpp содержащий подпрограммы:
- Spline2dCoeff – расчет коэффициентов кубических сплайнов таблично заданной функции.
- Progon3– решение СЛАУ методом прогонки
- Spline2d – вычисление значений функции в заданной точке на основе ее сплайн интерполяции
- Spline1d – построение одномерного интерполяционного кубического сплайна
2. Программа main1.cpp для построения двумерной сплайн модели
3. Программа main2.cpp расчет коэффициентов сплайн-интерполяции и вывод в фаил сплайн модели
4. Программа main3.cppдля расчета графика функции.
В результате использование данных программ была получена сплайн функция которая использовалась для построения зависимости выходного сигнала от температуры и давления (Рис.7.):
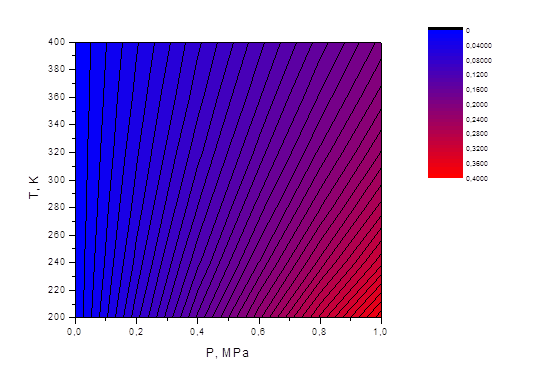
Рис. 7. Двумерная сплайн-интерполяция зависимости выходного сигнала от температуры и давления.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.