Разработка программы "Тензорный калькулятор", страница 6

Если поворот отсутствует, а имеет место только перенос центра отсчета параллельно осям координат, матрица поворота превращается в единичную.

В кристалле в силу трансляционной симметрии параллельный перенос начала координат на целое число узлов кристаллической решетки дает эквивалентную систему отсчета, значимым является только поворот, поэтому полагаем X₀ = 0 и

                 

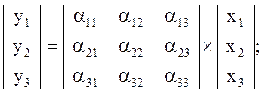
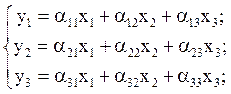
Математический смысл элементов матрицы A:  представляет собой косинус угла между новой осью координат  и старой :

Обратная связь между X и Y выражается через транспонированную матрицу A^T:

Правильно построенная матрица A должна удовлетворять следующим требованиям:

1)  Произведение прямой и транспонированной матрицы поворота представляет собой единичную матрицу:                            

2)  Определитель матрицы поворота равен единице (если обе системы координат правосторонние).

На этих свойствах может основываться контроль правильности задания матрицы поворота, если она задается вручную.

Реализация в программе:

1)  создадим 2 матрицы, задающие разные системы координат

2)  Создаем матрицу поворота выбрав в листе операций матрица поворота

3)  Создаем новую матрицу и копируем туда значения матрицы поворота (правой кнопкой копировать)

4)  Транспонируем матрицу поворота (правой кнопкой матрица данных)

5)  Перемножаем матрицу поворота и транспонированную матрицу поворота получается единичная матрица (с учетом погрешности). Значит теория верна

Матрицы можно найти в папке Пример 1;

2. Преобразование тензора при  повороте системы координат

При преобразовании системы координат изменяются и компоненты тензора. Если преобразование задано матрицей поворота A, то в новой системе координат компоненты тензора :

                                                       

В развернутом виде эта формула выглядит следующим образом:

                                        

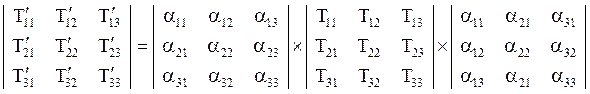
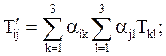
При записи операций тензорной алгебры принято опускать знаки суммирования, предполагая вычисление сумм по повторяющимся индексам; тогда можно записать в более компактном виде:

        

Реализация в программе:

Метод непосредственного преобразования (умножение матриц)                           

1)  Создаем тензор 3х3 в матричной форме

2)  Загружаем  матрицу перехода из прошлого примера

3)  Копируем и транспонируем ее

4)  Умножаем матрицу поворота на тензор

5)  Полученный результат умножаем на транспонированную матрицу перехода

Упрощенный метод:

1)  Загружаем тензор и матрицу перехода (тензор может быть представлен как в матричной, так и в одноиндексной форме.)

2)  В списке операций выбираем «преобразование тензора 2-го ранга к новой системе координат»

Результаты по двум методам одинаковые. См. папку Пример 2.

3. Тензор механического напряжения

В реальных упругих состояниях механическое напряжение выражается тензором второго ранга. Тензор второго ранга представляет собой совокупность девяти значений, которые характеризуют некоторую физическую величину, зависящую от направления в трехмерном пространстве. Компоненты тензора второго ранга обычно записываются в виде матрицы 3х3:

                                               

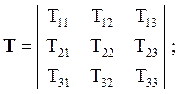
Скалярное значение тензорной величины T в направлении , заданном вектором направляющих косинусов, может быть вычислено по формуле:

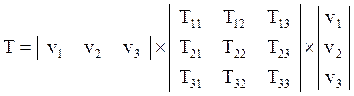                                       или

, где верхний индекс ^Т означает операцию транспонирования. В результате транспонирования вектор-столбец превращается в вектор-строку.

Операция умножения выполняется справа налево. После умножения  получается вектор-столбец, умножая на который  получаем их скалярное произведение, оно и представляет собой значение тензорной величины в заданном направлении.

Реализация в программе:

Реализовать можно также двумя методами, при упрощеннм виде есть функция «тензор одноосного напряжения в произвольной системе координат»       .