Разработка программ с циклами. Циклы с постусловием и предусловием. Операторы continue и break, страница 2

Операторы continue и break могут быть использованы в любом из трех типов циклов и позволяют оптимизировать их исполнение.

                   

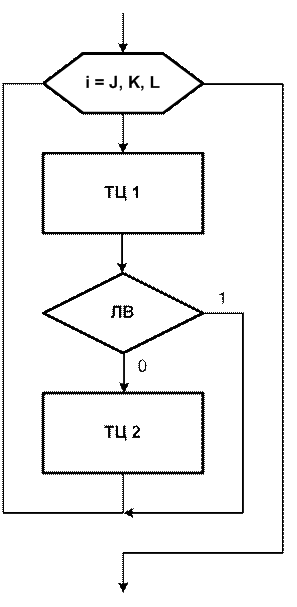
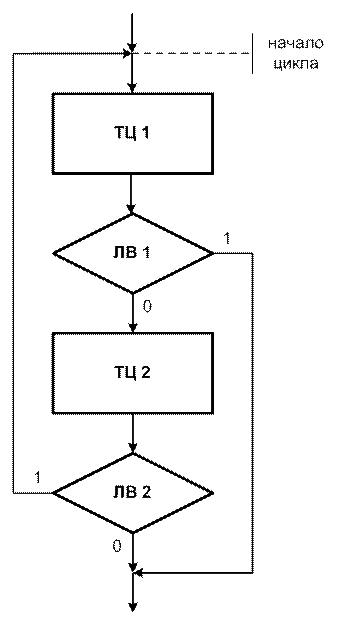
Рис. 3.4. Цикл for с оператором              Рис. 3.5. Цикл do-while

continue                      с оператором break

5. Примеры использования простейших циклов

Некоторые примеры программ, использующих простейшие циклы, приведены в подразделе  Examples\  03 Циклы \ 3 Примеры циклов. Ряд программ достаточно просты и предназначены для самостоятельного анализа. Поясним лишь наиболее сложную программу, реализующую метод простых итераций для решения нелинейных уравнений. Она представлена в различных вариантах в файлах ex030330.cpp, ex030332.cpp, ex030335.cpp и ex030337.cpp.

Уравнение  , где  - левая часть, не допускающая возможности решить это уравнение аналитически, может быть решено методом последовательных приближений (итераций). Для этого его нужно предварительно привести к виду:    . Отсюда вытекает простая итерационная формула

,                                                                            (3.1)

где     k = 1, 2, 3, … - номер итерации. Нулевое приближение  - задается, а затем осуществляются итерации по формуле (3.1). Для очень многих уравнений итерационный процесс сходится, т.е. каждое последующее значение  все ближе и ближе приближается к значению корня уравнения. В качестве условия прекращения итераций обычно используют

,                                                                          (3.2)

где      - заданное заранее значение погрешность определения корня.

На рис. 3.6 приведена блок-схема алгоритма, выполняющего метод простых итераций с помощью цикла с постусловием. Она реализована в программе, находящейся в файле ex030330.cpp. Сначала задаются значения входных переменных X0 и e (на блок-схеме не показано). Затем выполняются начальные установки: переменной X присваивается значение X0, а счетчик циклов k обнуляется. В теле цикла сначала выполняется инкремент счетчика, а затем вычисляется новое приближение корня  Xnew по итерационной формуле (3.1). Перед выполнением операции переприсваивания X = Xnew  выполняется вычисление разности DX,  которая необходима для проверки условия повторений итераций. Условие повторения представляет собой  противоположное условию (3.2).

При реализации цикла с предусловием необходимо, чтобы при первом вхождении в цикл величина DX имела значение, обеспечивающее его выполнение. Это реализуется оператором начального присваивания  DX = 2e.

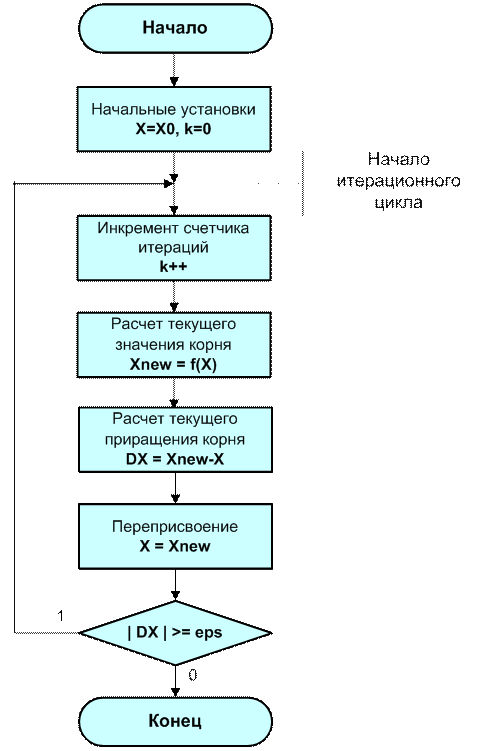
Рис. 3.6. Блок-схема алгоритма метода простых итераций

Входные переменные:             X0      - нулевое приближение корня;

eps     - абсолютная погрешность вычисления  корня.

Выходные переменные: X        - значение корня;

                                                  k        - число выполненных итераций.

Внутренние переменные:        k        - номер текущей итерации;    

Xnew - значение корня, получаемое на текущей итерации;

DX     - разность значений корня, полученных на текущей итерации и на предыдущей.

6. Задание к работе

1.  Проанализировать и исполнить программы подразделов for, while и примеры циклов каталога Examples\03 Циклы). На приведенных примерах освоить синтаксис операторов циклов и особенности их использования.

2.  Разработать программу для расчета сумм и произведения

2.1.         ;          ;                   .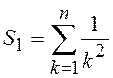

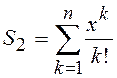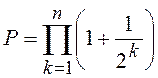2.2.         ;          ;   .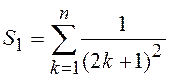

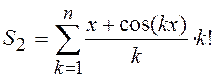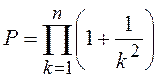2.3.         ;            ;      .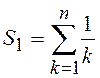

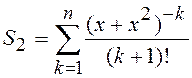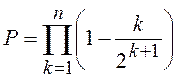2.4.         ;  ;             .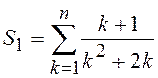

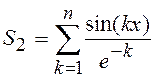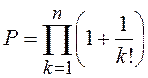2.5.         ;  ;           .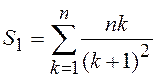

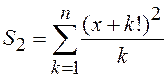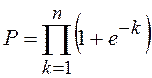2.6.         ;   ;         .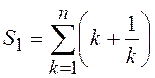

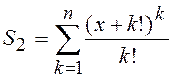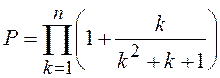2.7.         ;;                   .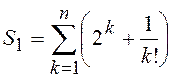

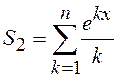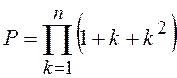2.8.         ;   ;               .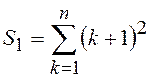

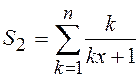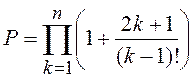3.  Разработать программу для вывода на дисплей и нахождения суммы целых чисел, находящихся в интервале от n до m:

3.1. всех простых чисел;

3.2. всех, делящихся на три, пять и семь без остатка.

4.  Разработать программы для расчета бесконечной суммы. Суммирование следует прекращать, когда очередное слагаемое по абсолютной величине станет меньше заданной погрешности . Выполнить в двух вариантах: с циклом с постусловием и с предусловием. В программах предусмотреть подсчет и вывод выполненного числа циклов.

4.1.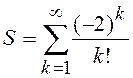     

4.2.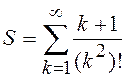     

4.3.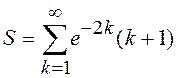     

4.4.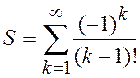     

4.5.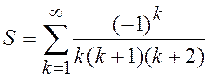     

4.6.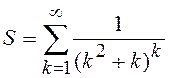     

4.7.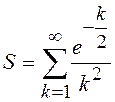      

4.8.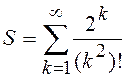     

5.  На основе аналога, реализующего метод простых итераций (ex030330.cpp и ex030332.cpp), разработать программу для решения уравнения    методом Ньютона. Этим методом корень уравнения находится по заданному нулевому приближению  последовательными приближениями по формуле:

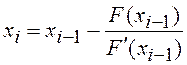;       где     i = 1, 2, 3, … - номер итерации.

Итерации следует прекращать, когда будет выполнено условие ; где  - заданная погрешность.

Проверить работу программы на решении уравнений    

                     и        .

6.  Разработать программу для расчета и вывода на экран монитора таблицы зависимости    в пределах от  до  с шагом  (x и y – вещественные).  Выполнить три варианта: цикл с предусловием, цикл с постусловием и цикл по вещественной переменной.