Задание № 6. В данном задании требовалось проанализировать и исполнить программы Murka раздела switch (часть Ветвления) и освоить синтаксис оператора switch и особенности его использования.
Задание № 7. В данном задании требовалось разработать
программу, присваивающую трем переменным 
, 
и 
значения параметров одного их
трех полупроводниковых материалов: германия, кремния или арсенида галлия, в
зависимости от введенного ключа выбора G, S или A.
|
Материал |
|
|
|
|
германий |
16.0 |
0.67 |
2.4.1013 |
|
кремний |
11.9 |
1.12 |
1.45.1010 |
|
арсенид галлия |
13.1 |
1.43 |
1.79.106 |
Затем должны выполняться вычисления величин
;
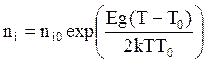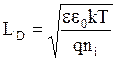, где q = 1.60.10-19 Кл – заряд электрона;
e0 = 8.85.10-14 Ф/см – диэлектрическая постоянная;
k = 8.62.10-5 эВ/К – постоянная Больцмана.
В конце
работы программа должна выводить значения величин 
и 
на дисплей.
Расчет выполняется для значения температуры, заданного преподавателем.
Входные данные: T,T0,ni0,Eg,eps; тип - doublе(вещественные переменные); eps0=8.85E-14,q=1.6E-19,k=8.62E-5; тип - const doublе
Выходные данные: ni, Ld; тип –doublе(вещественные переменные).
Текст программы:
#include <iostream.h>
#include <conio.h>
#include <math.h>
#include <stdio.h>
void main()
{
char M;
double ni,Ld,T,T0,ni0,Eg,eps;
const double eps0=8.85E-14,q=1.6E-19,k=8.62E-5;
int key=0;
clrscr();
cout<<"Введите название материала М – ‘G’, ‘S’ или ‘A’ "; cin>>M;
cout<<endl;
switch(M)
{
case 'G':
eps=16,Eg=0.67,ni0=2.4E13;
cout<<" eps=16"<<endl;
cout<<" Eg=0.67"<<endl;
cout<<" ni0=2.4E13"<<endl;
break;
case 'S':
eps=11.9,Eg=1.12,ni0=1.45E10;
cout<<" eps=11.9"<<endl;
cout<<" Eg=1.12"<<endl;
cout<<" ni0=1.45E10"<<endl;
break;
case 'A':
eps=13.1,Eg=1.43,ni0=1.79E6;
cout<<" eps=13.1"<<endl;
cout<<" Eg=1.43"<<endl;
cout<<" ni0=1.79E6"<<endl;
break;
default:
cout<<endl<<"Такое значение М не предусмотрено!"<<endl;
eps=0;
Eg=0;
ni0=0;
key=1;
}
if(!key)
{
cout<<"T=";
cin>>T;
cout<<"T0=";
cin>>T0;
ni=ni0*exp(Eg*(T-T0)/2*k*T*T0);
Ld-sqrt(eps*eps0*k*T/q*ni);
cout<<"ni="<<ni<<endl;
cout<<"Ld="<<Ld<<endl;
}
Else cout<<endl<<" Такое значение М не предусмотрено! "<<endl;
getch();
}
Результаты исполнения работы:
Набор 1. Введите название матеpиала M - 'G' или 'S' или 'A' G
eps=16
Eg=0.67
ni0=2.4E13
T=0
T0=5
ni=2.4e+13
Ld=2.710317e-256
Нажмите Enter
Набор 2. Введите название матеpиала M - 'G' или 'S' или 'A' H
Такое значение M не предусмотрено!
Такое значение М не пpедусмотpено!
Нажмите Enter
Набор 3. Введите название матеpиала M - 'G' или 'S' или 'A' A
eps=13.1
Eg=1.43
ni0=1.79E6
T=60
T0=0
ni=1790000
Ld=1.084196e-255
Нажмите Enter
Вывод:
Была разработана программа, присваивающая трем переменным , и значения
параметров одного их трех полупроводниковых материалов: германия, кремния или
арсенида галлия, в зависимости от введенного ключа выбора G, S
или A.
При написании использовали операторы if, switch() default.Результаты исполнения работы приведены после текста программы. Программа успешно работает.
Задание № 8. В данном задании требовалось разработать программу для вычисления корней кубического уравнения. Формульное описание алгоритма приведено в Приложении 1 и файле Root3_alg_text.doc, а его блок-схема – в Приложении 2 и файле Root3_alg_block.doc. Отладить работу всех ветвей программы с помощью тестовых данных, приведенных в Приложении 3 и файле Root3data.doc.
Входные данные: a,b,c,d ;тип - doublе(вещественные переменные).
Внутренние переменные: p,q,D,y1,y2,y3,z,k,fi,u,v,w, r; тип - doublе(вещественные переменные).
Выходные данные: x1,x2,x3; тип – doublе(вещественные переменные).
Блок-схема алгоритма решения кубического уравнения:
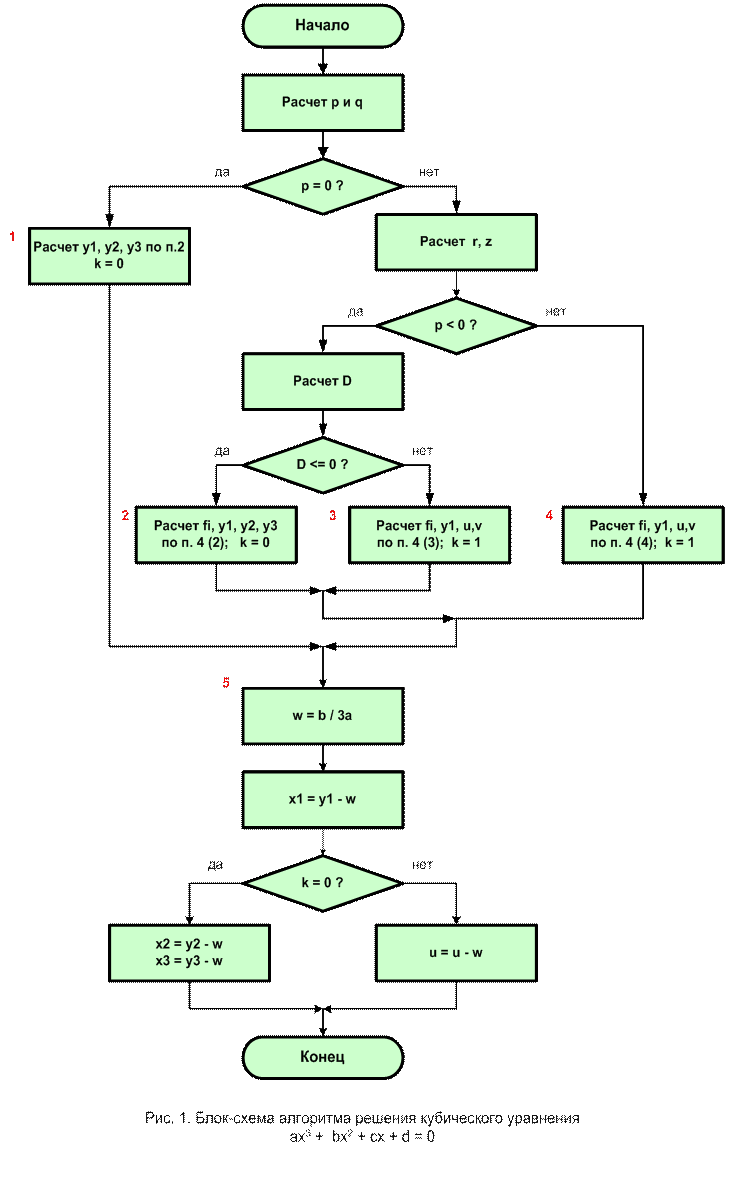
Текст программы:
#include <conio.h>
#include <iostream.h>
#include <math.h>
void main()
{
double a,b,c,d,p,q,D,y1,y2,y3,z,k,fi,u,v,w,x1,x2,x3,r;
clrscr();
D=0; r=0; z=0; fi=0; u=0; v=0; y2=0; y3=0;
cout<<"a = "; cin>>a;
cout<<"b = "; cin>>b;
cout<<"c = "; cin>>c;
cout<<"d = "; cin>>d;
p=(3*a*c-b*b)/(9*a*a);
q=(2*b*b*b/(27*a*a*a)-b*c/(3*a*a)+d/a)/2;
if (p==0) {
y1=pow(-2*q,1./3.);
y2=y1;
y3=y1;
k=0;
}
else {
if (q<0) r=-pow(fabs(p),1./2.);
else r=pow(fabs(p),1./2.);
z=q/(r*r*r);
if (p<0) {
D=q*q+p*p*p;
if (D<=0) {
fi=acos(z);
y1=-2*r*cos(fi/3);
y2=2*r*cos(M_PI/3-fi/3);
y3=2*r*cos(M_PI/3+fi/3);
k=0;
}
else {
fi=log(z+sqrt(z*z-1));
y1=-2*r*cosh(fi/3);
u=r*cosh(fi/3.0);
v=sqrt(3.)*r*sinh(fi/3.0);
k=1;
}
}
else {
fi=log(z+sqrt(z*z+1));
y1=-2*r*sinh(fi/3);
u=r*sinh(fi/3.0);
v=sqrt(3.)*r*cosh(fi/3.0);
k=1;
D=q*q+p*p*p;
}
}
w=b/3/a;
x1=y1-w;
if (k==0) {
x2=y2-w;
x3=y3-w;
}
else {
x2=u-w;
x3=v;
}
cout<<"x1="<<x1<<endl;
cout<<"x2="<<x2<<endl;
cout<<"x3="<<x3<<endl;
getch();
}
Результаты исполнения работы:
Набор 1. a = 2.0
b = 3.0
c = 1.5
d = -15.75
x1=1.5
x2=1.5
x3=1.5
Набор 2. a = 1.5
b = -3.0
c = -7.5
d = 9.0
x1=-2
x2=3
x3=1
Набор 3. a = 1.0
b = 4.0
c = -12.75
d = 7.5
x1=-6.237038
x2=1.338954
x3=0.898085
Набор 4. a = 2.0
b = -10.0
c = 18.0
d = -10.0
x1=1
x2=2
x3=1
Вывод: Была разработана программа для вычисления корней кубического уравнения.
При написании использовали операторы if, if - else.Результаты исполнения работы приведены после текста программы. Программа успешно работает.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
, эВ
, см-3