Разработка программ с ветвлениями (Лабораторная работа № 2), страница 5

6. Литература

1. Березин Б.И., Березин С.Б. Начальный курс С и С++. М.: «Диалог-МИФИ», 1997 – 2005.

2. Подбельский В.В. Фомин С.С. Программирование на языке Си. М.: Финансы и статистика. 1999 - 2005.

3. Подбельский В.В. Язык C++. М.: Финансы и статистика. 1999 - 2005.

4. Климова Л.М.. Основы практического программирования на языке Си. М.: Издательство ПРИОР, 1999, 464 с.

1). Вычислить

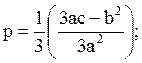
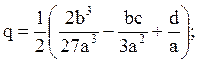
2). Если p = 0, то вычислить и перейти к п. 5.

3) Если , то нужно вычислить (знак r совпадает со знаком q);

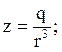
4). Если , то нужно вычислить D

Дальнейшие действия зависят от знаков p и D:

Ветвь 2	Ветвь 3	Ветвь 4
Все корни вещественные	Один корень вещественный, а два - комплексные
p<0



;

5). Вычислить корни

- если все корни вещественные, то i = 1, 2, 3.

- если корни комплексные, то

где .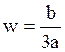

Примечание:

Обратные функции можно вычислить по формулам

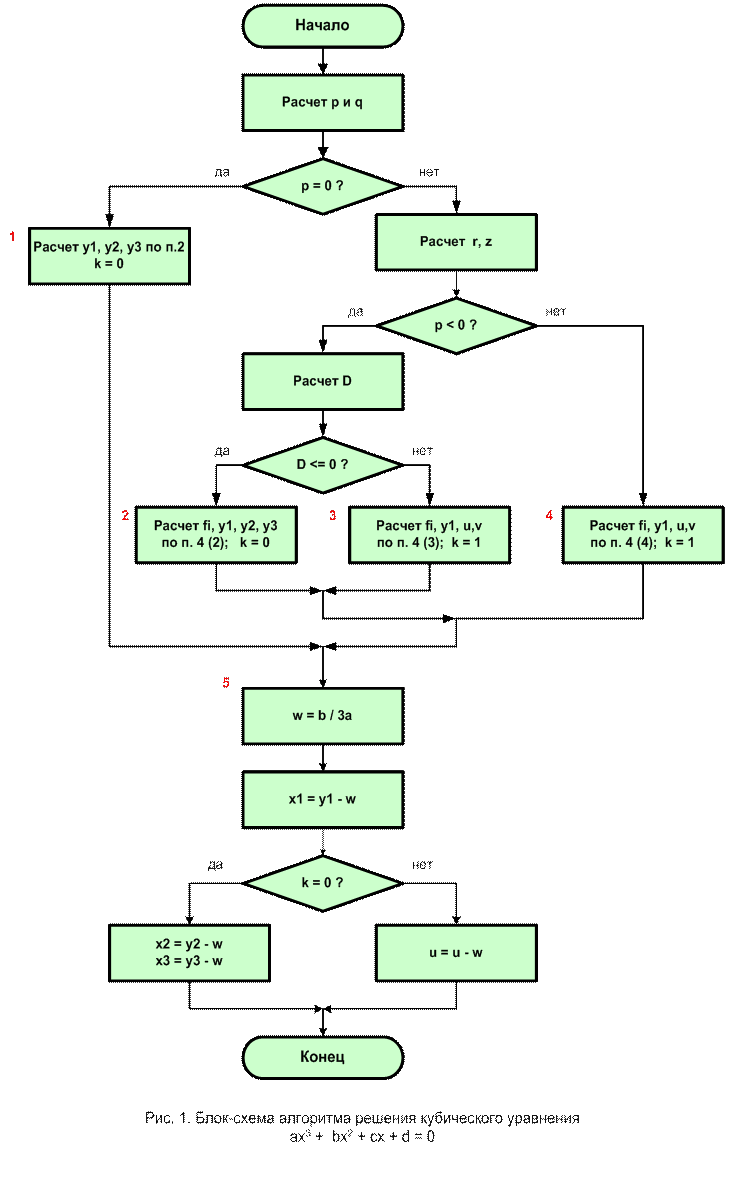
для программы Root3

(решение кубического уравнения ax³ + bx² + cx + d = 0)

Значения промежуточных переменных для четырех тестовых примеров Root3

(решение кубического уравнения ax³ + bx² + cx + d = 0)

1 2 3 4 5