Информатика и выч. техника \ Информатика

Разработка программ с циклами. Разработка программы для расчета сумм и произведения, страница 2

clrscr();

cout<<"eps=";

cin>>eps;

fact=1;

S=0;

for (k=1; ;k++)

{

fact=fact*k;

if(fabs(pow(-2,k)/fact)<eps)

break;

S=S+pow(-2,k)/fact;

cout<<" S="<<S<<endl;

}

getch();

}

Результаты исполнения работы:

Набор 1.

eps=1E-30

S=-2

S=0

S=-1.333333

S=-0.666667

S=-0.933333

S=-0.844444

S=-0.869841

S=-0.863492

S=-0.864903

S=-0.864621

S=-0.864672

S=-0.864664

S=-0.864665

Набор 2.

eps=1E-10

S=-2

S=0

S=-1.333333

S=-0.666667

S=-0.933333

S=-0.844444

S=-0.869841

S=-0.863492

S=-0.864903

S=-0.864621

S=-0.864672

S=-0.864664

S=-0.864665

Вывод: Для расчета бесконечной суммы 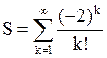была разработана программа с ветвлением. Требовалось, чтобы суммирование прекращалось, когда очередное слагаемое по абсолютной величине станет меньше заданной погрешности . При написании использовали операторы for и if. Результаты исполнения работы приведены после текста программы. Программа успешно работает.

Задание № 6. В данном задании требуетсяразработать программу для решения уравнения методом Ньютона.Корень уравнения находится по заданному нулевому приближению последовательными приближениями по формуле

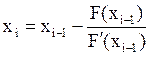; где i = 1, 2, 3, … - номер итерации.

Итерации следует прекращать, когда будет выполнено условие ; где - заданная погрешность.

Проверить работу программы на решении уравнений и .

Входные данные: X0, eps, DX, Xnew, F, F1; тип – doublе(вещественные переменные).

Выходные данные: X; тип – doublе(вещественные переменные).

k; тип – int(целые переменные).

Текст программы:

#include <iostream.h>

#include <stdio.h>

#include <conio.h>

#include <math.h>

void main()

{

int k;

double X0,eps,X,DX,Xnew,F,F1;

clrscr();

cout<<"eps = "; cin>>eps;

cout<<" X0 = "; cin>>X0;

X=X0;

k=0;

printf("\nk X DX\n\n");

{

k++;

F=cos(X)-X;

F1=-sin(X)-1;

//F=pow(eps,-X)-X;

//F1=-pow(eps,-X)-1;

DX=F/F1;

X=X-DX;

//Xnew=cos(X);

//DX=Xnew-X;

//X=Xnew;

printf("%2d %10.6f %10.6f\n",k,X,DX);

getch();

}

while (fabs(DX)>=eps);

cout<<endl;

cout<<"X = "<<X<<endl;

cout<<"k = "<<k<<endl;

getch();

}

Результаты исполнения работы:

Набор 1.

eps = 1E-2

X0 = 1

k X DX

1 0.750364 0.249636

2 0.739113 0.011251

3 0.739085 0.000028

X = 0.739085

k = 3

Набор 2.

eps = 1E-10

X0 = 1

k X DX

1 0.750364 0.249636

2 0.739113 0.011251

3 0.739085 0.000028

4 0.739085 0.000000

5 0.739085 0.000000

X = 0.739085

k = 5

Вывод: Для решения уравнения методом Ньютона Корень была разработана программа с ветвлением. Уравнение должно было находится по заданному нулевому приближению последовательными приближениями по формуле

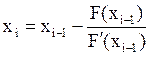; где i = 1, 2, 3, … - номер итерации.

Требовалось прекращать итерации, когда будет выполнено условие ; где - заданная погрешность, а так же проверить работу программы на решении уравнений и .

При написании использовали операторы for и if. Результаты исполнения работы приведены после текста программы. Программа работает.

Задание № 7. В данном задании требуетсяразработать программу для расчета и вывода на дисплей таблицы зависимости

в пределах от до с шагом (x и y – вещественные).

Использовать цикл с предусловием, цикл с постусловием и цикл по вещественной переменной.

Входные данные: Xmin, Xmax, Xstp, y1; тип – doublе(вещественные переменные).

Выходные данные: x, y; тип – doublе(вещественные переменные).

Текст программы:

#include <iostream.h>

#include <stdio.h>

#include <conio.h>

#include <math.h>

void main()

{

double Xmin,Xmax,Xstp,x,y,y1;

clrscr();

cout<<"Xmin = "; cin>>Xmin;

cout<<"Xmax = "; cin>>Xmax;

cout<<"Xstp = "; cin>>Xstp;

cout<<endl;

y1=1;

x=Xmin;

printf(" x y=f(x)\n\n");

for (x=Xmin; x<=Xmax; x+=Xstp){

// do

//{x+=Xstp;

y=y1*(2*x);

printf("%5g %7g\n",x, y); }

// while (x<=Xmax);

getch();

}

Результаты исполнения работы:

Набор 1.

Xmin = 1

Xmax = 6

Xstp = 1

x y=f(x)

1 2

2 4

3 6

4 8

5 10

6 12

Набор 2.

Xmin = 7

Xmax = 15

Xstp = 2

x y=f(x)

7 14

9 18

11 22

13 26

15 30

Вывод: Для расчета и вывода на дисплей таблицы зависимости

в пределах от до с шагом (x и y – вещественные)

была разработана программа с ветвлением.

При написании использовали операторы for и if. Результаты исполнения работы приведены после текста программы. Программа успешно работает.

1 2

Скачать файл