cout<<endl;
if (pow((x-x1),2)+pow((y-y1),2) <= r_1*r_1) k1=1; else k1=0;
if (pow((x-x_2),2)+pow((y-y_2),2) <= r_2*r_2) k2=1; else k2=0;
if ( k1 && k2 ) cout<<"Точка принадлежит и первому и второму кругу";
else if ( k1 && !k2 ) cout<<"Точка принадлежит первому кругу";
else if ( !k1 && k2 ) cout<<"Точка принадлежит второму кругу";
else cout<<"Точка не принадлежит ни одному из кругов";
getch();
}
|
Материал |
|
|
|
|
германий |
16.0 |
0.67 |
2.4.1013 |
|
кремний |
11.9 |
1.12 |
1.45.1010 |
|
арсенид галлия |
13.1 |
1.43 |
1.79.106 |
Затем должны выполняться вычисления величин
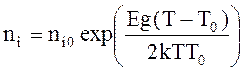 ;
;
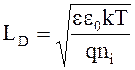 ,
,
где q = 1.60.10-19 Кл – заряд электрона;
e0 = 8.85.10-14 Ф/см – диэлектрическая постоянная;
k = 8.62.10-5 эВ/К – постоянная Больцмана.
В конце
работы программа должна выводить значения величин ![]() и
и ![]() на дисплей.
на дисплей.
Расчет выполняется для температур T = 200, 300 и 400 К.
Если
пользователь неправильно ввел значения ключа, переменным ![]() ,
, ![]() и
и ![]() должны быть
присвоены нулевые значения, вычисления
должны быть
присвоены нулевые значения, вычисления ![]() и
и ![]() не выполняться, а в качестве результата
выводиться соответствующее сообщение.
не выполняться, а в качестве результата
выводиться соответствующее сообщение.
#include <iostream.h>
#include <conio.h>
#include <math.h>
void main()
{
//Описание данных
const double q=1.6e-19, eps_0=8.85e-14, k=8.62e-5, T_0=293;
double eps,E_g,n_i0,n_i,L_d,T;
char kod;
int err=0;
//присвоение
clrscr();
cout<<"Введите T "; cin>>T;
cout<<"Введите КОД материала (g/s/a) "; cin>>kod;
switch (kod)
{
case 'g': case 'g':
eps=16;
E_g=0.67;
n_i0=2.4e+13;
break;
case 's': case 's':
eps=11.9;
E_g=1.12;
n_i0=1.45e+10;
break;
case 'a': case 'a':
eps=13.1;
E_g=1.43;
n_i0=1.79e+6;
break;
default:
cout<<"Ошибка - "; err=1;
eps=0;
E_g=0;
n_i0=0;
}
if (!err)
{
//Расчет
n_i=n_i0*exp(E_g*(T-T_0)/2/k/T/T_0);
L_d=sqrt(eps*eps_0*k*T/q/n_i);
// Вывод
cout<<"n_i= "<< n_i <<endl;
cout<<"L_d= "<< L_d<<endl;
} else cout<<”Введён неверный код”<<endl;
getch();
![]()
1). Вычислить
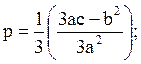
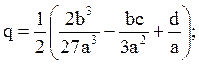
2). Если p = 0, то вычислить ![]() и перейти к п. 5.
и перейти к п. 5.
3) Если ![]() , то нужно вычислить
, то нужно вычислить ![]() (знак r совпадает
со знаком q);
(знак r совпадает
со знаком q);
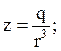
4). Если ![]() , то нужно вычислить D
, то нужно вычислить D
![]()
Дальнейшие действия зависят от знаков p и D:
|
Ветвь 2 |
Ветвь 3 |
Ветвь 4 |
|
Все корни вещественные |
Один корень вещественный, а два - комплексные |
|
|
p<0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5). Вычислить корни
- если все корни вещественные, то ![]()
![]() i = 1, 2, 3.
i = 1, 2, 3.
- если корни комплексные, то ![]()
![]()
![]() где
где 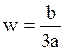 .
.
Примечание:
Обратные функции можно вычислить по формулам
![]()
![]()
#include <iostream.h>
#include <conio.h>
#include <math.h>
void main()
{
//®ЇЁб ЁҐ ¤ ле
double a,b,c,d,p,q,r,z,D,w,phi,u,v,x[3],y[3];
int complsqr;
//ЇаЁбў®ҐЁҐ
clrscr();
cout<<"aX+bX+cX+d = 0"<<endl<<endl;
cout<<"ўўҐ¤ЁвҐ = "; cin>>a;
cout<<"ўўҐ¤ЁвҐ b= "; cin>>b;
cout<<"ўўҐ¤ЁвҐ c= "; cin>>c;
cout<<"ўўҐ¤ЁвҐ d= "; cin>>d;
//а бзсв
w=b/3/a;
p=((3*a*c-b*b)/(3*a*a))/3;
q=(2*pow(b,3)/27/pow(a,3)-b*c/3/a/a+d/a)/2;
if (p==0)
{ // k=0 ‚ᥠЄ®аЁ ўҐйҐб⢥лҐ
complsqr=0;
y[0]=y[1]=y[2]=pow(-2*q,1/3.);
for (int i=0; i<=2; i++) x[i]=y[i]-w;
} else
{// k !=0
r=sqrt(fabs(p)); if (q<0) r=-r;
z=q/pow(r,3);
if (p<0)
{
D=q*p+p*p*p;
if (D<=0)
{ // p<0 D<=0 ‚ᥠЄ®аЁ ўҐйҐб⢥лҐ
phi=acos(z);
y[0]=-2*r*cos(phi/3);
y[1]= 2*r*cos(M_PI/3 - phi/3);
y[2]= 2*r*cos(M_PI/3 + phi/3);
for (int i=0; i<=2; i++) x[i]=y[i]-w;
complsqr=0;
} else
{ // p<0 D>0 …бвм Є®¬Ї«ҐЄблҐ Є®аЁ
phi=log(z+sqrt(fabs(z*z-1)));
y[0]=-2*r*cosh(phi/3);
u=r*cosh(phi/3);
v=sqrt(3)*r*sinh(phi/3);
x[0]=y[0]-w;
x[1]=x[2]=u-w;
y[2]=2*r*cos(M_PI/3 + phi/3);
complsqr=1;
}
} else
{ // p>0 …бвм Є®¬Ї«ҐЄблҐ Є®аЁ
phi=log(z+sqrt(fabs(z*z+1)));
y[0]=-2*r*sinh(phi/3);
u=r*sinh(phi/3);
v=sqrt(3)*r*cosh(phi/3);
x[0]=y[0]-w;
x[1]=x[2]=u-w;
complsqr=1;
}
}
//‚лў®¤
if (complsqr)
{
cout<<"x1"<<" = "<<x[0]<<endl;
cout<<"z2"<<" = "<<x[1]<<" + i* "<<v<<endl;
cout<<"z3"<<" = "<<x[2]<<" - i* "<<v<<endl;
} else
{
for (int i=0; i<=2; i++) cout<<"x"<<i+1<<" = "<<x[i]<<endl;
}
getch();
}
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.