Данная лабораторная работа посвящена упражнениям в разработке функций. Разрабатываются две из перечисленного в задании списка функций (по указанию преподавателя), а также управляющие программы (главные функции), позволяющие их оттестировать и отладить. При разработке функций необходимо стремиться к наибольшей их универсальности, реализовывать эффективные алгоритмы и проявлять хороший стиль программирования. В необходимых случаях следует использовать готовые функции из раздела Examples\ 08 Готовые модули.
2. Готовые модули
2.1. Модуль Matrix. Содержит функции для работы с матрицами:
2.1.1. InpMat() – ввод матрицы с клавиатуры;
2.1.2. OutMat() – вывод матрицы на экран монитора;
2.1.3. MultMat() – умножение двух матриц;
2.1.4. DegMat() – возведение матрицы в целую степень;
2.1.5. NormMat() – вычисление нормы матрицы.
2.2. Модуль Linsys. Содержит одну функцию - LinGauss () – решение системы линейных алгебраических уравнений методом Гаусса;
2.3. Модуль Integral. Содержит функцию SdxSimps() – вычисление определенных интегралов методом Симпсона.
2.4. Модуль Root. Содержит одну функцию - RootNewton() – решение нелинейных уравнений методом Ньютона.
Все эти модули представляют собой упрощенные варианты одноименных, используемых в третьей части дисциплины «Информатика» в следующем семестре. Подробное описание заголовков входящих в модули функций приводится в Приложении 2.
Дополнительно используется функция Root3(), предназначенная для решения кубических уравнений.
Выполняются два задания из приводимого перечня (по указанию преподавателя).
1. Разработать функцию для расчета
обратного гиперболического тангенса 
на основе решения уравнения 
.
Решение
уравнения осуществить с помощью функции RootNewton() с погрешностью 
.
Примечание: Следует учитывать, что функция 
может принимать значения от –1 до +1,
следовательно этот интервал будет областью возможных значений аргумента 
.
2. Разработать функцию для поиска в
вещественной матрице 
элемента, наиболее близкого по
значению к заданному 
В выходных данных должно быть само значение этого близкого элемента, а также номера строк и столбцов, в которых он расположен.
3. Разработать функцию для расчета
площади замкнутой фигуры, ограниченной на интервале 
сверху
и снизу функциями 
и 
.
.
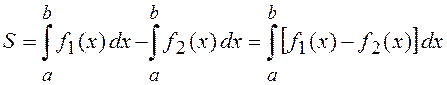Для вычисления интегралов использовать функцию SdxSimps().
Проверить разработанную функцию на примере вычисления площади круга
при 
и 
.
4. Разработать функцию для подсчета числа каждого символов, встречающихся в одномерном символьном массиве. Проверить работу функции на массиве, случайным образом заполненном большими латинскими буквами (коды символов от 65 до 90).
5. Разработать функцию для
упорядочивания элементов в матрице (тип элементов –
вещественный), в результате которого значения элементов должны возрастать как
по строкам, так и столбцам.
6. Значение некоторой функции 
может быть вычислено по рекуррентной
формуле
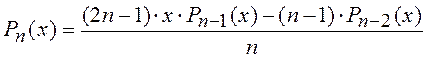, при
, а 
.
Разработать функцию для расчета .
7. Разработать функцию для расчета
матричной экспоненты 
. Алгоритм расчета матричной
экспоненты может быть основан на ее разложении в степенной ряд 
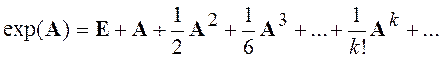, где E - единичная матрица.
Суммирование
следует прекращать, когда норма очередного слагаемого станет меньше заданной
погрешности 
..
Для возведения матрицы в степень использовать функцию DegMat(), а для расчета нормы – NormMat() из модуля Matrix.
8. Разработать функцию для обработки списка
…
Петров Иван Иванович
Михайлов Сергей Петрович
Ковалева Анна Андреевна
…
Обработка должна заключаться в перестановке места фамилии; в результате должен получиться список
…
Иван Иванович Петров
Сергей Петрович Михайлов
Анна Андреевна Ковалева
…
При разработке функции использовать технику указателей.
9. Разработать функцию для
упорядочивания элементов в матрице 
(тип элементов –
вещественный), в результате которого строки матрицы должны быть переставлены
так, чтобы средние значения элементов по строкам возрастали бы от первой
строки до последней.
10.Разработать функцию для расчета
коэффициента корреляции между двумя вещественными одномерными массивами 
и 
,
содержащими n элемен-тов.
Коэффициент корреляции 
рассчитывается по формуле:
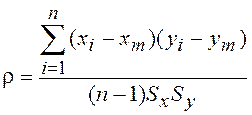, где 
и 
- средние значения; 
и 
-
среднеквадратичные отклонения элементов соответствующих массивов. Значения 
и считаются
по формулам:
; 
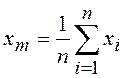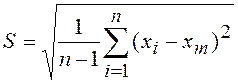; значения и - по аналогичным формулам.
11.Разработать функцию, генерирующую все
возможные наборы значений n логических переменных 
в виде массива целых 0 или 1. Например,
для n = 3 должна генерироваться совокупность наборов:
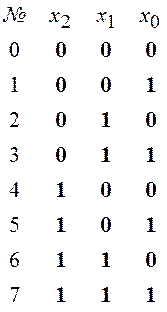
12. Разработать модуль-функцию для
нахождения собственных значений матрицы 
.
Собственные значения – корни уравнения
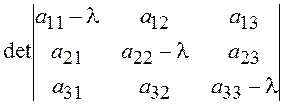
Для решения возникающего кубического уравнения использовать готовую функцию из предыдущей лабораторной работы.
13. Разработать функцию для расчета
вырожденной гипергеометрической функции 
на
основе ее представления в виде бесконечного ряда:
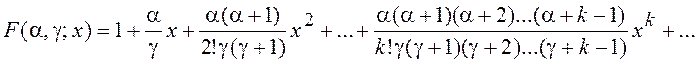
Суммирование
можно прекратить, когда очередное слагаемое станет меньше заданной погрешности 
.
14. Разработать функцию для поиска в
вещественной матрице элемента, который наименее
отличается от среднего значения всех элементов матрицы.
15. Разработать функцию для установки заданной длины строки путем равномерной вставки дополнительных пробелов между словами.
16. Разработать функцию для расчета по заданной матрице A (m-строк, n-столбцов) матрицы B, представляющей собой произведение исходной матрицы на ее же транспонированную:
17. Разработать функцию для выбора из матрицы с вещественными числами с m строк и n столбцов всех положительных элементов и записи их в одномерный массив в порядке следования строк и столбцов.
Проверить работу функции на матрице, заполненной случайными числами, лежащими в диапазоне от -10 до +10.
18. Разработать функцию для переписывания элементов вещественной квадратной симметричной матрицы в одномерный массив (по строкам) и функцию для обратного преобразования – формирования квадратной симметричной матрицы из одномерного массива.
Пример:
Из матрицы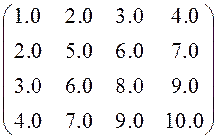 
должен сформироваться массив
Вторая функция должна выполнить обратное преобразование.
19. Разработать функцию для нахождения
матрицы, обратной заданной, на основе следующего алгоритма, основанного на
решении матричного уравнения 
, где A - исходная, B – обратная ей
и E - единичная матрицы:
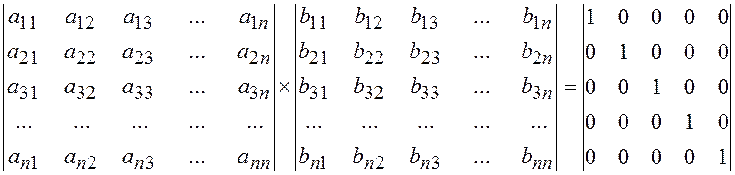
Это уравнение при умножении матрицы A на каждый столбец матрицы B распадается на n систем линейных алгебраических уравнений (СЛАУ):
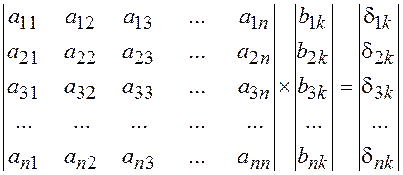, где
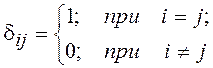(k 1,2, …, n)
Решение каждой системы при k =1, 2 , ..., n позволяет определить k-тый столбец искомой обратной матрицы, т.е. процедура нахождения обратной матрицы сводится к n-кратному решению СЛАУ. Этот метод называется методом Жордана.
Для решения СЛАУ использовать функцию LinGauss(), для вывода результата на экран – функцию OutMat() (модуль matrix.cpp).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
