Краткие методические указания по работе с модульным учебным комплексом по электротехнике МУК-ЭТ, страница 7

Методические указания и рекомендации

Для исследуемого последовательного колебательного контура характеристическое уравнение:

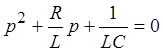
имеет два корня

 

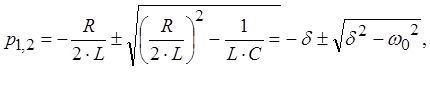
где d =  - коэффициент затухания;

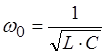 - угловая резонансная частота контура.

Если d > w₀ т.е. сопротивление цепи относительно велико, то корни p₁ и p₂ вещественны, и в цепи переходный процесс будет иметь апериодический характер. Если d=w₀, т.е. R=R_кр=2 , то корни характеристического уравнения одинаковы и вещественны, и это соответствует предельному случаю апериодического переходного процесса. Если же d< w₀, то

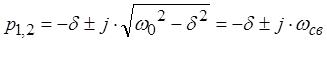   , где w_св= - угловая частота собственных затухающих колебаний контура.

О скорости затухания свободного процесса в контуре можно судить по логарифмическому декременту колебания, равному натуральному логарифму отношения двух следующих друг за другом максимальных значений тока (напряжения) одного знака:

.

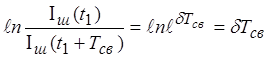Отсюда  -  экспериментальное определение d (Рис. 10.2):

;

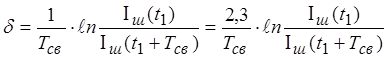w_св = .

                i

 

t₁                                                                     t

 

    I_ш(t₁+T_св)

I_ш(t₁)

T_св

Рис. 10.2.

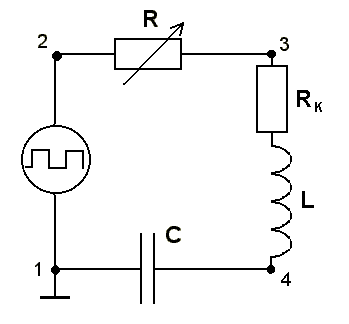
Рис. 10.1.

Лабораторная работа  №11

Исследование нелинейной катушки индуктивности

Цель работы: Изучить электромагнитные явления в цепи катушки с ферромагнитным сердечником и зависимость ее параметров от величины приложенного напряжения.

Рабочее задание

1.  Соберите схему Рис.11.1. Рекомендуется использовать в качестве нелинейной катушки индуктивности первичную обмотку трансформатора T_p, а в качестве сопротивления резистор R₁=27 Ом. Установите частоту генератора 50¸80 Гц. На первый канал осциллографа подайте напряжение с концов сопротивления R (U_R=U_{2 3}), а на второй канал - сигнал со звукового генератора (U_ВХ=U_{1 2}).

2.  Постепенно увеличивая напряжения U_ВХ с шагом ~ 2 В в пределах от 0 до 15 В, измерьте напряжение U_R и фазовый сдвиг j между этим напряжением и U_ВХ. Для этих измерений используйте осциллограф. Обратите внимание на экране осциллографа на прогрессирующее искажение формы кривой тока в катушке (напряжение на R) при увеличении подаваемого напряжения U_ВХ.

3.  Разобрав схему, проведите измерение сопротивления катушки R_K . Для этого соберите схему Рис. 11.2. Плавно увеличивая сигнал генератора постоянного напряжения, установите его таким, чтобы сила тока через катушку не превышала ~ 100 мА (во избежание ее нагрева). Измерив силу тока и напряжения, вычислите, пользуясь законом Ома, сопротивление  R_K.

4.  По результатам пп.2,3 вычислите

-  ток в катушке I;

-  косинус сдвига фаз cosj;

-  мощность, потребляемую катушкой P;

-  мощность потерь в обмотке («потери в меди») P_M;

-  мощность потерь в стальном сердечнике («потери в стали») P_C;

-  эквивалентные сопротивления R_Э, X_Э, L_Э.

5.  На одном графике постройте зависимости тока, потребляемой мощности, мощности потерь в обмотке и в сердечнике, эквивалентных активного и реактивного сопротивлений и коэффициента мощности катушки от величины напряжения на катушке.

6.  Для одного из значений напряжения на катушке (на выбор), пренебрегая током рассеяния, постройте векторную диаграмму катушки и определите параметры ее схемы замещения. Нарисуйте схему замещения катушки.

Методические указания и рекомендации

к пункту 4

Ток в катушке можно вычислить с помощью закона Ома

;

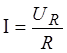Сдвиг фаз j между напряжением U_K и I определяется как сдвиг фаз между осциллографами U_K и U_R с помощью осциллографа;

Мощность, потребляемая катушкой

;

Мощность потерь в обмотке

 ;

Мощность потерь в сердечнике

;

Эквивалентные сопротивления

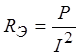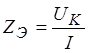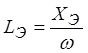; ; ;, где w - угловая частота.

к пункту 6.

Если пренебречь магнитным потоком рассеяния, то входное сопротивление идеализированной катушки , где 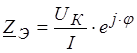 , тогда 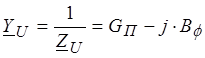, проводимости G_П и В_Ф образуют параллельные ветви схемы замещения, угол потерь .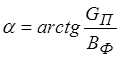

ЭДС самоиндукции катушки определяется графически из векторной диаграммы, построенной по известному напряжению на катушке U_К и напряжению U_R сопротивления R_К методом засечек. При этом для построения рекомендуется направлять вектор напряжения на R_К по вектору тока на диаграмме.