Г – произвольное термодинамическое свойство раствора.
![]() - парциальная молярная
величина первого компонента в растворе.
- парциальная молярная
величина первого компонента в растворе.
![]() - парциальная молярная
величина второго компонента в растворе.
- парциальная молярная
величина второго компонента в растворе.
![]() ;
;
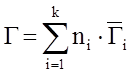 –
многокомпонентный раствор.
–
многокомпонентный раствор.
Пример: ![]()
![]()
![]()
![]()
 §4.Основные методы определения
парциальных молярных величин.
§4.Основные методы определения
парциальных молярных величин.
![]()
![]() ;
;
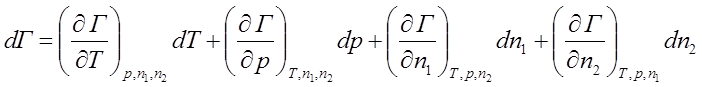 ;
;
![]() ;
;
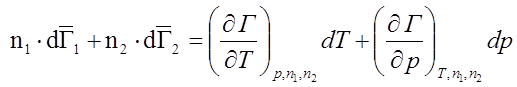 ;
;
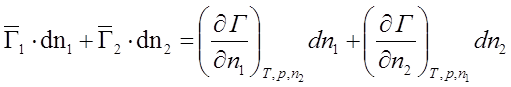 ;
;
1) T = const; Þ dT = 0; p = const; Þ dp = 0.
![]() – уравнение Гиббса-Дюгема. Следовательно,
парциальные молярные величины компонентов в растворе взаимосвязаны.
– уравнение Гиббса-Дюгема. Следовательно,
парциальные молярные величины компонентов в растворе взаимосвязаны.
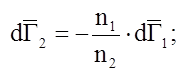
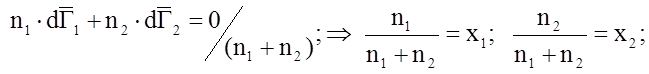
![]() – другая форма уравнения Гиббса-Дюгема.
– другая форма уравнения Гиббса-Дюгема.
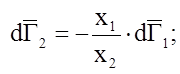
![]()
2) n2 = const; Þ dn2 = 0;
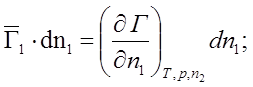
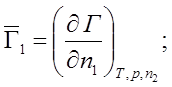
n1 = const; Þ dn1 = 0;
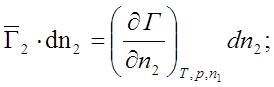
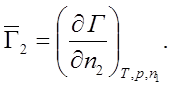
Метод касательной:
![]() ; Т,р º const; n2 = const;
n1.
; Т,р º const; n2 = const;
n1.
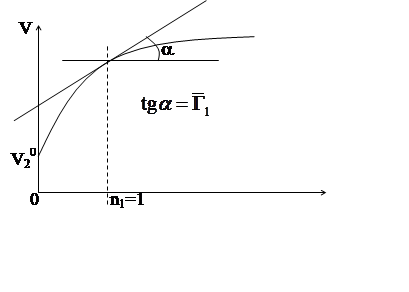
![]()
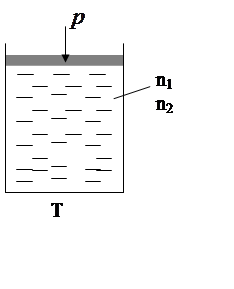
При
n1 = 0; ![]()
n2 = 1 моль;
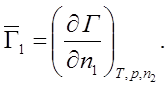
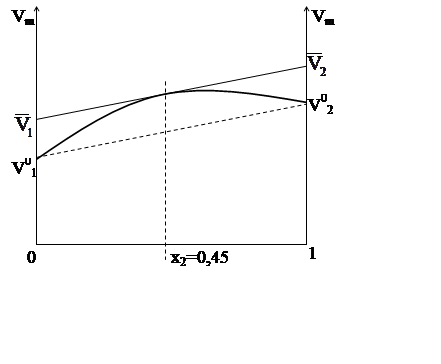 Метод
отрезков на осях:
Метод
отрезков на осях:
![]()
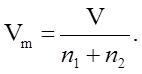
§5.Связь химического потенциала с парциальными молярными величинами.
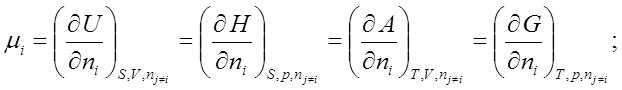
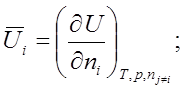
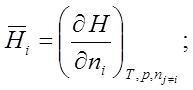
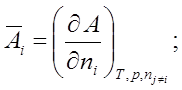
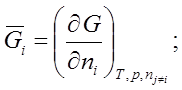
![]()
![]() ; по ni при Т, р, nj¹i º const.
; по ni при Т, р, nj¹i º const.
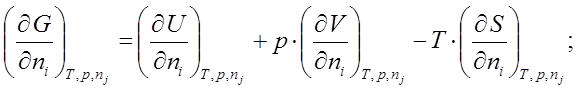
![]()
![]()
![]()
![]()
Химическая термодинамика.
§6. Термодинамические свойства вещества.
1) Масса (m) – кг, г, мг
2) Количество вещества (n) – моль
1 моль – это такое количество вещества, которое содержит число частиц, равное числу Авогадро.

3) Давление (p) – Па, атм, мм.рт.ст.
1 атм = 101325 Па = 760 мм.рт.ст.
4) Объем (V) – м3, л, мл
1л=103мл=1дм3; 1дм3=103см3; 1мл=1см3.
5) Температура
Термодинамическая шкала температуры: T, К
Практическая шкала температуры: t, oC
1 К=![]()
T=273,15+t oC
DT=Dt
6) Уравнение состояния
f(p,V,T)=0
Уравнение Менделеева-Клапейрона:
PV=nRT, R-универсальная газовая постоянная
Уравнение состояния справедливо как для чистых газов, так и для смеси.
7) Закон Дальтона для смеси идеальных газов
|
|
|
|
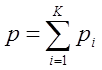
|
Молярная доля – это количество вещества компонента в одном моле смеси.
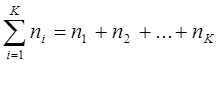
|
|
|
§7. Термодинамические уравнения.
Уравнение первого закона термодинамики:
dU=dQ-dW, dU – бесконечно малое изменение внутренней энергии или полный дифференциал внутренней энергии.
![]() dQ
– бесконечно малое количество тепла, поглощенного или отданного веществом при
процессе, эта величина не является полным дифференциалом, поэтому обозначается d.
dQ
– бесконечно малое количество тепла, поглощенного или отданного веществом при
процессе, эта величина не является полным дифференциалом, поэтому обозначается d.
dW – бесконечно малая работа вещества в процессе.
dW=dWмех+dWнемех
Wмех – работа по изменению объема вещества.
dWмех=pdV
dWнемех – это все виды работы, не попадающие под Wмех (электрическая, работа химической реакции).
Wх.р.=ZFE, Z- количество электронов, принимающих участие в электрохимическом процессе; F – число Фарадея; E – ЭДС гальванического элемента.
dU=dQ-pdV-dWнемех
|
|
DU – изменение внешней энергии системы при переходе из первого состояния во второе. |
DU=U2-U1
U1 - внешняя энергия системы в первом состоянии;
U2 - внешняя энергия системы во втором состоянии.
При переходе из первого состояния во второе внешняя энергия может изменяться:
а) DU>0, U1<U2
б) DU<0, U1>U2
в) DU=0, U1=U2
Энтальпия.
Энтальпия – функция состояния, равная сумме внутренней энергии и потенциальной энергии всестороннего сжатия системы.
H – энтальпия, H=U+pV
PV – потенциальная энергия всестороннего сжатия системы
dH=dU+pdV+Vdp
dH=dQ-pdV-dWнемех+pdV+Vdp
dH=dQ-dWнемех+Vdp – 2-ая форма 1-го закона термодинамики
DH=Qp-Wнемех, Qp – тепловой эффект химической реакции
Wнемех=0, DH=Qp, DH=H2-H1
1) H1<H2, DH>0, Qp>0 – эндотермическая реакция
2) H1>H2, DH<0, Qp<0 – экзотермическая реакция
3) H1=H2, DH=0, Qp=0 – атермическая реакция
U=U(T, V)
H=H(T, p)
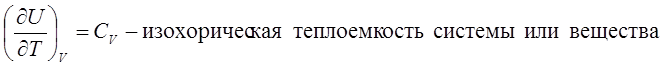
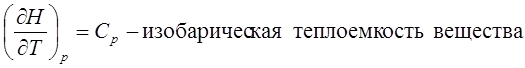
CV>0, Cp>0, при увеличении температуры обе функции только возрастают
Обратимые и необратимые процессы.
Термодинамический процесс называется обратимым, если при его протекании параметры состояния изменяются бесконечно малыми порциями.
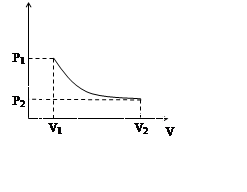
|
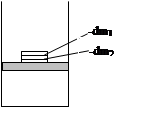
Процесс, при котором прямой и обратный пути перехода из одного состояния в другое совпадают, называется обратимым.
При необратимом процессе параметры изменяются конечными порциями.
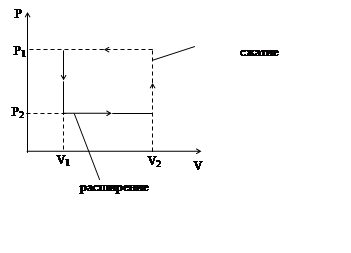
Все формы уравнения первого закона термодинамики одинаково применимы к обратимым и необратимым процессам.
Основные принципы термодинамики.
1) Принцип возрастания энтропии
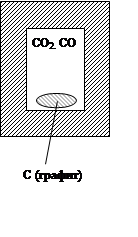
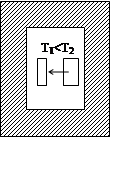

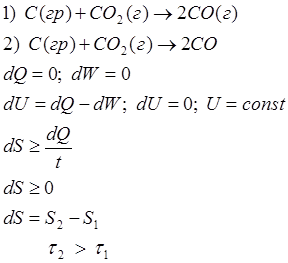
1) самопроизвольный процесс
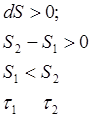
2) состояние устойчивого равновесия
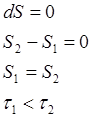
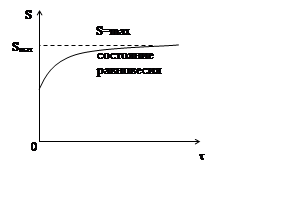
В изолированной системе из всех возможных процессов самопроизвольно протекает процесс, при котором энтропия системы только увеличивается. В состоянии устойчивого равновесия энтропия изолированной системы максимальна.
DrS – изменение энтропии при химической реакции
DrS>0, значит данная реакция в изолированной системе будет протекать самопроизвольно
DrS<0, самопроизвольно реакция в изолированной системе протекать не может
DrS=0, в изолированной системе реакция в состоянии равновесия
Признак уменьшения энергии Гельмгольца.
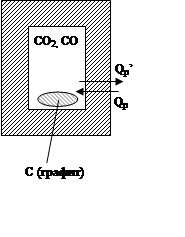
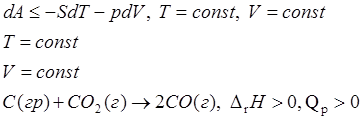
![]()
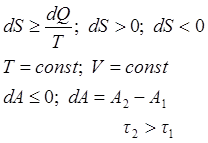
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.