Численное моделирование процесса формирования структуры отливки: Методические указания к выполнению лабораторной работы по курсу «Моделирование процессов и объектов в металлургии», страница 2

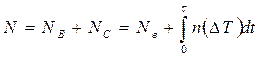
Для полиэдрической структуры средний размер зерна можно определить соотношением   

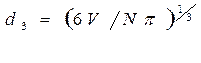
Математическая модель кристаллизации сплава

Совокупность формул (1) - (3) описывает процесс кристаллизации металла или сплава, затвердевающего при постоянной температуре t_кр , от которой отсчитывается текущее переохлаждение DТ (рисунок 2, а):

.

Для сплавов, кристаллизующихся в температурном интервале                                              (рисунок 2, б), переохлаждение необходимо отсчитывать от температуры ликвидуса t_л остаточной жидкой фазы, состав которой меняется по мере выделения твердой фазы:

         .                                                          (4)

Без значительной погрешности можно принять, что линия ликвидуса бинарной диаграммы состояния является прямой с угловым коэффициентом р , то  есть

.                                    (5)

где  С₀ - исходный состав сплава; С_ж -  текущей состав жидкой фазы.

С учетом (5) уравнение (4) приобретает вид:

                         (6)

Состав жидкой фазы С_ж(t) однозначно связан с количеством m и средним составом С_т(t) выделившейся твердой фазы . Если состав твердой и жидкой фазы связаны между собой постоянным коэффициентом распределения примеси , тогда можно записать соотношение

,                                                        (7)

справедливое при равномерном распределении примеси в объеме каждой из фаз.

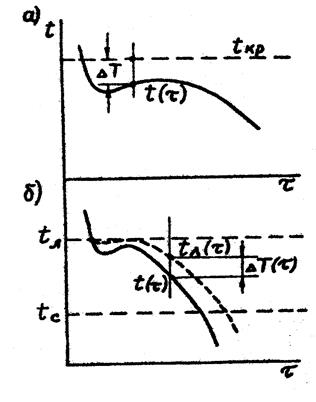
Рисунок 2 - Процесс кристаллизации сплавов: а – затвердевающих при постоянной температуре; б – затвердевающих в интервале температур.

Следует оговорить, что состав жидкой фазы С_ж изменяется не только во времени в связи с изменением количества твердой фазы, но и по сечению отливки, имеющей неравномерное распределение температуры, переохлаждения, количества твердой фазы и т.д. Строгое решение задачи возможно лишь с учетом не только тепловых, но также диффузионных и конвективных процессов, определяющих локальный состав жидкой фазы. Однако полное решение подобной задачи является делом будущего. Как показывают опыты, достаточно хорошее приближение можно получить, не рассматривая явления молекулярного и конвективного переноса примеси, т.е. на основе уравнения теплопроводности   

                                                                          (8)

где l - теплопроводность металла;  r - пространственная координата; b - коэффициент, определяющий конфигурацию  отливки (значения b^0,5 = 0,1,2 соответствуют плоской, цилиндрической или шаровой отливке); с(t) – объемная теплоемкость металла в жидком (С_ж), твердом (С_т) состоянии или в период кристаллизации:

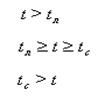
С(t) =                     

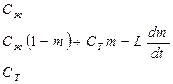
Начальное условие задается в виде исходного равномерного распределения температуры заливки металла t_зал  . Граничные условия на поверхности раздела металла – форма (t = t_n  при r = R, где t_n –температура поверхности формы) могут быть заданы в форме: 

             ,                                                 (9a)

отвечающей охлаждению металла в тонкостенном металлическом кокиле по закону Ньютона с коэффициентом теплоотдачи a в среде с температурой t_ср или в виде:

                        ,                                                (9б)

соответствующем теплоотводу в неметаллическую (песчаную) форму с тепловой активностью b_ф и начальной температурой t_н .

Уравнения (1) – (3) и (4) – (9) образуют замкнутую систему, описывающую тепловые и кристаллизационные явления (на макроуровне) в отливке, и составляют в совокупности математическую модель процесса затвердевания и формирования макроструктуры. Аналитическое решение этой системы получить невозможно, в связи с чем задача решается численным методом с использованием ЭВМ.