Моделирование систем массового обслуживания с отказами и ограниченной очередью, страница 3

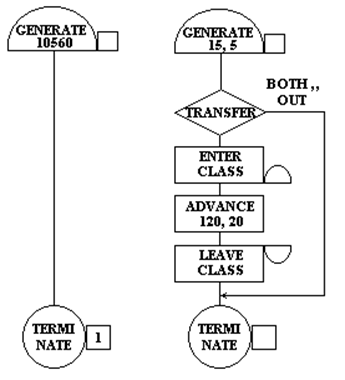
Рис. 6.1 – Блок – диаграмма GPSS-модели

Составление программы модели производится на основании исходных данных и определенной ранее последовательности блоков. Программа имитации системы приведена на рис. 6.2.

Рис. 6.2 – Программа имитации работы дисплейного класса

Выходные данные программы после выполнения программы документирования результатов работы модели можно просмотреть в файле REPORT.GPS. Для анализа результатов моделирования приведем статистическую информацию о многоканальном устройстве CLASS:

Анализ результатов моделирования. На основании данных, полученных в результате моделирования работы дисплейного класса, можно сделать следующие выводы:

§  в течение месяца дисплейный класс посетили 698 студентов;

§  среднее содержимое МКУ CLASS равно 7,83 – это говорит о том, что в среднем было занято 8 компьютеров из 10 имеющихся, коэффициент загрузки дисплейного класса – 0,783;

§  количество необслуженных заявок определим как разность между числом транзактов, вышедших из блока GENERATE и числом транзактов, вошедших в блок ADVANCE (либо как разность между значениями вхождений транзактов в блоки TERMINATE и LEAVE): 703 – 698 = 695 – 690 = 5, т.е. 5 студентов покинули класс, из-за того, что все компьютеры были заняты в момент их прихода;

§  вероятность того, что заявка останется необслуженной (процент необслуженных заявок), определим как отношение числа необслуженных заявок к общему числу поступивших заявок: 5 / 703 = 0,007 (0,7 % заявок не были обслужены).

6.5  Пример моделирования одноканальной СМО с ограниченной очередью

Постановка задачи. Вычислительный центр некоторого предприятия предназначен для решения задач, возникающих в различных цехах и отделах предприятия. Время поступления задач на вычислительный центр распределено равномерно; параметры распределения – m = 10 минут, r = 4 минуты; время решения задачи также распределено равномерно с параметрами m = 15 минут, r = 3 минуты. Размер очереди задач на вычислительном центре ограничен 16 единицами. Если при поступлении задачи очередь заполнена, то задача отправляется на альтернативный вычислительный центр, где расценки за решение задач значительно выше (такие задачи следует считать не решенными). Необходимо смоделировать работу вычислительного центра в течение месяца (22 восьмичасовых рабочих дня), собрать информацию о параметрах очереди, количестве решенных и не решенных задач.