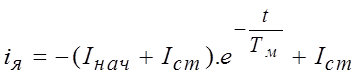Электромеханические свойства ЭМС на основе двигателей постоянного тока независимого возбуждения, страница 3

, а в случае отсутствия нагрузки имеем 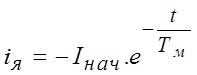  . Интегрирование приведенных выражений дает формулы для вычисления времени торможения. При торможении до любого значения скорости, например до ω₁ , время вычисляется по выражению

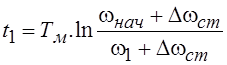, а в случае торможения до полной остановки, т. е. до ω₁=0, по выражению

.

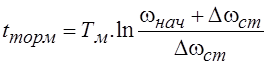Оценим эффективность динамического торможения, т. е. оценим изменение значения замедления (интенсивность замедления), анализом характеристик, приведенных на рис.     . Он показывает, что  в зависимости от сопротивления торможения R_торм  характеристики динамического торможения имеют различный наклон и это позволяет получать в момент перехода на режим торможения различное значение момента торможения. Чем больше сопротивление динамического торможения (R_торм.2 > R_торм.1), тем меньше момент динамического торможения (М_дин.1 > М_дин.2). По мере снижения скорости значение момента торможения уменьшается (М_i), а следовательно, уменьшается интенсивность торможения. При работе электропривода с активным моментом нагрузки процесс динамического торможении не оканчивается при скорости равной нулю. Активный момент заставляет якорь двигателя поменять направление вращения и разогнаться до скорости, при которой М_дв.т =М_ст. На рис.     это до скорости –ω_кон.1 при R_торм.1 и до скорости –ω_кон.2 при R_торм.2. Поэтому в такого типа электроприводах при использовании динамического торможения для окончательной остановки необходимо предусмотреть отключение электропривода при достижении скоростью нулевого значения.

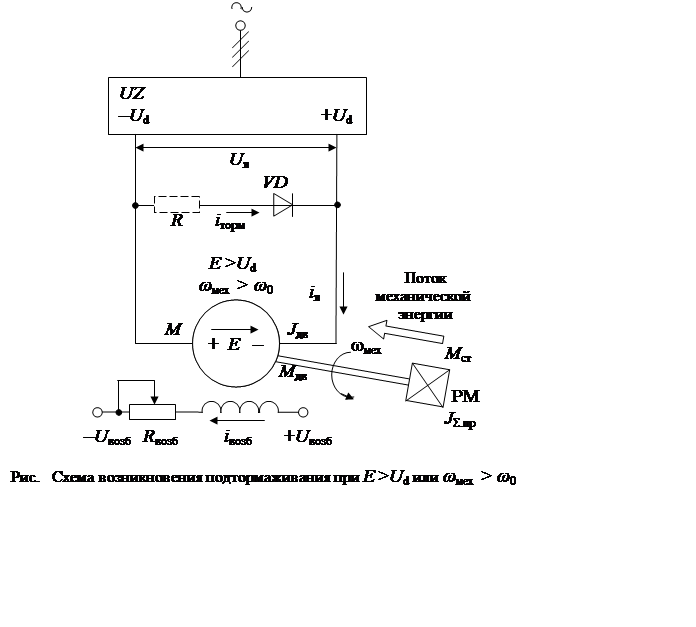
В электроприводах с управляемыми полупроводниковыми выпрямителями для создания подтормаживающего эффекта в процессе торможения за счет уменьшения питающего двигатель напряжения, когда ЭДС двигателя становится больше напряжения U_d на выходе выпрямителя, вводится в действие диод с возможно включенным последовательно ему сопротивлением, создающие контур для тока торможения, рис.       .

Искусственные механические характеристики другого свойства можно получить, использую второй канал управления двигателем постоянного тока, а именно, изменение  магнитного потока машины (тока возбуждения).  В связи с тем, что рабочая точка состояния магнитной цепи двигателя      выбирается    в     так     называемом     колене     его     кривой  

 

намагничивания, то увеличение потока будет связано с насыщением магнитной цепи, что является с энергетической точки зрения не желательным. Поэтому регулирование выполняется за счет уменьшения (ослабления) магнитного потока. Это приводит к увеличению скорости идеального холостого хода ω₀ и к уменьшению момента короткого замыкания М_к.з. соответственно и модуль жесткости статической механической характеристики уменьшится пропорционально квадрату потока   . 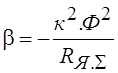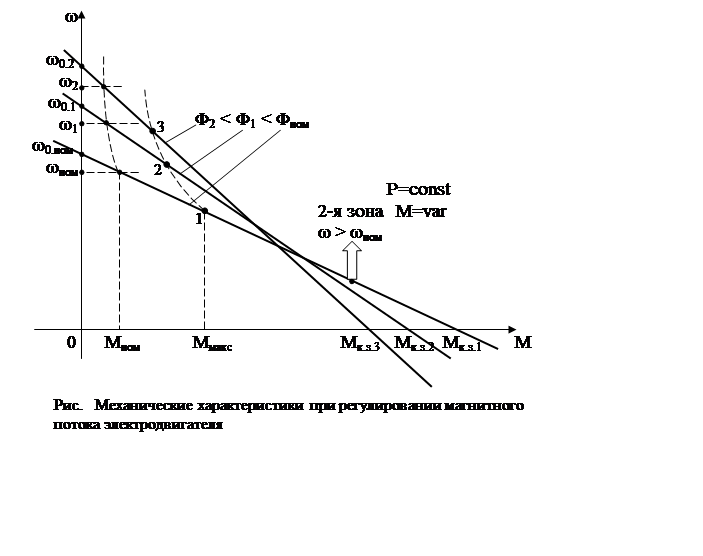Механические характеристики при таком управлении приведены на рис.      . Диапазон регулирования скорости рассматриваемым способом небольшой D ≤ 3…4. Это объясняется тем, что предел увеличения скорости ограничивается механической прочностью узлов двигателя. Для двигателя постоянного тока максимальная скорость не превышает 4000 об/мин. Рабочий участок характеристик (ω_0.ном – 1, ω_0.1– 2, ω_0.2 – 3) ограничивается перегрузочной способностью двигателя, которая уменьшается в силу уменьшения магнитного потока (М_дв = к · Ф · i_Я), рис.     . 

Способ регулирования за счет изменения добавочного сопротивления в якорной цепи двигателя в настоящее время мало используется из-за низкого качества регулировочных, пусковых и тормозных характеристик, больших технико-экономических затрат.

 

Вернемся к приведенным в начале уравнениям, описывающим работу двигателя, записав их в операторной форме

,

.

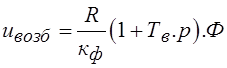где Т_в=L_в/R_в – электромагнитная постоянная времени обмотки возбуждения, Т_я=L_я/R_я – электромагнитная постоянная времени обмотки якоря, к_ф=Ф/i_в – коэффициент, соответствующий линейной части кривой намагничивания двигателя. На основании записанных уравнений можно составить структурную схему электропривода постоянного тока независимого возбуждения, рис.     . При работе двигателя с номинальным потоком (Ф = Ф_ном = const) структурная схема электропривода, поскольку имеем (1 + Т_я·р)·М=β·(ω₀ – ω), будет выглядеть как апериодическое звено первого порядка, рис.      .

 

                                                    

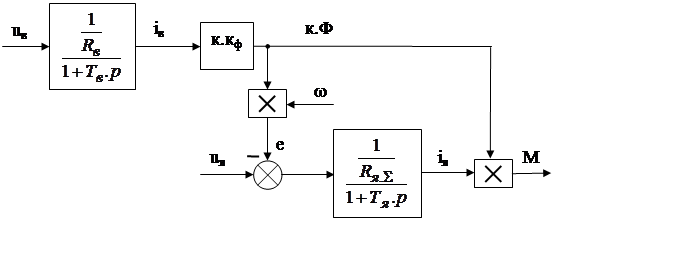
Рис.

    

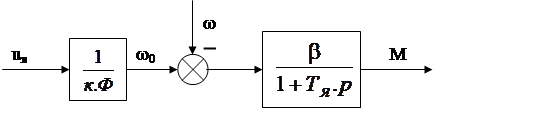
Рис.