








![]()
|
|
|
|
|

|
|
|
|
|
|

|
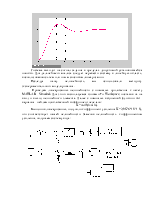
3.1.Расчет коэффициентов передаточной функции модели
Исследуемый технологический объект описывается системой уравнений:
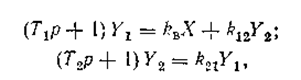
где коэффициенты определяются как:
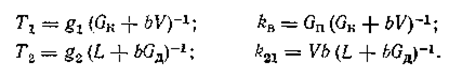
При этом передаточные функции получаются в виде:
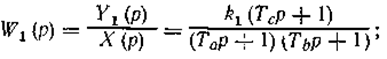
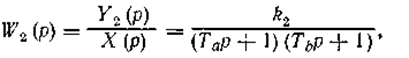
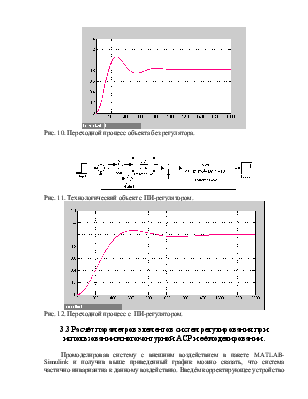
Пропорциональный регулятор с введением в закон регулирования интеграла (сокращенно ПИ- регуляторы).
Эти регуляторы перемещают регулирующий орган пропорционально сумме отклонения и интеграла от отклонения регулируемой величины:
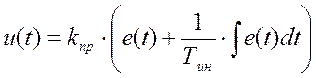
В динамике ПИ- регулятор соответствует системе из двух параллельно включенных звеньев: пропорционального с коэффициентом передачи k и интегрирующего с коэффициентом передачи T.
Передаточная функция ПИ- регулятора:
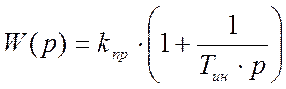
Порядок подбора ПИ-регулятора на основании желаемого показателя колебательности.
Согласно теории автоматического управления для замкнутой системы, которая имеет показатель колебательности М, можно в комплексной плоскости построить амплитудо-фазо-частотную характеристику разомкнутой системы, которая будет касаться окружности с центром на отрицательной действительной оси в точке
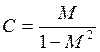
и радиусом
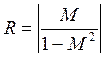 .
.
Исходя из этих условий, используется следующий алгоритм расчёта параметров регулятора на желаемую величину М:
1.
Из начала координат комплексной
плоскости проводится луч под углом ![]() относительно
отрицательной вещественной оси. Этот луч является касательной к ранее названной
окружности.
относительно
отрицательной вещественной оси. Этот луч является касательной к ранее названной
окружности.
2. Строится амплитудо-фазо-частотная характеристика объекта регулирования с условным регулятором, с коэффициентом передачи равным 1
3. Для ПИ-регулятора строим амплитудо-фазо-частотную характеристику объекта с учётом интегральной части регулятора
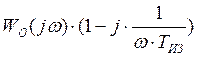
где Тиз выбирается из некоторого ряда характерного для промышленных регуляторов (1,5,10,50,100,300).
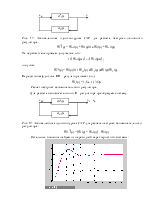
4. Далее строится окружность с центром на действительной оси, которая касается луча и амплитудо-фазо-частотной характеристики.
5. Находим значение L как расстояние от мнимой оси до точки касания окружности с лучом и рассчитываем коэффициент пропорциональной части регулятора
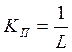
6.
Если амплитудо-фазо-частотная
характеристика плохо пересекает луч, то необходимо ввести масштабный
коэффициент ![]() , на который умножаем
амплитудо-фазо-частотную характеристику. В этом случае коэффициент пропорциональной
части регулятора рассчитывается по следующей формуле
, на который умножаем
амплитудо-фазо-частотную характеристику. В этом случае коэффициент пропорциональной
части регулятора рассчитывается по следующей формуле
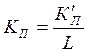
Рассчитаем коэффициенты усиления
|
T куба=137,2 °С; |
Vвч=116,87 м3/ч; |
Lнч=244,74 м3/ч; |
|
TL ЛВГ 0=242,6 °С; |
Vнч=221,52 м3/ч; |
Lвч=79,05 м3/ч; |
Sфл.ем.=7,11 м2
Sкуб.кол.= 270,3 м2
Найдем постоянные времени Ti и константы kj согласно действующим параметрам колонны.
Согласно базисным величинам постоянные времени Ti и константы kj имеют следующие значения:
Тс=0,061ч=219,6с. k1=0,147
Та=0,065ч=223,78с k2= 1,241
Тв=0,065°С=208,34с
Подставив постоянные времени Ti и константы kj в систему уравнений получаем систему дифференциальных уравнений в численной форме:
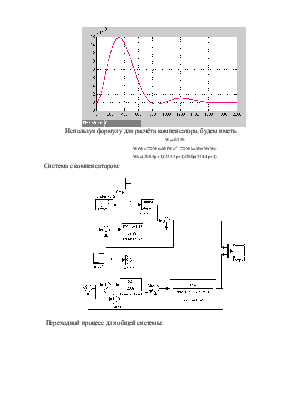
W1=0.147(219,6+1)/( 223,78p+1)( 208,34 p+1)
W2=1.241/(223,78+1)( 208,3+1)
Для расчета регулятора найдём эквивалентную передаточную функцию объекта:
![]()
![]()
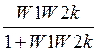
![]()
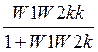
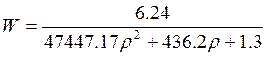
Получили эквивалентную передаточную функцию объекта относительно второго выхода.
3.2 Расчёт параметров элементов систем регулирования при использовании локальных АСР и её моделирование.
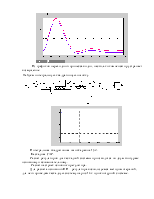
После моделирования получили Кп=0,3, а Ти=200
Передаточная функция регулятора
Wрег=0,3+0,3/200p
Промоделируем систему с регулятором и без него, используя приложение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.