Синтез системы автоматического управления технологическим процессом регулирования температуры материала в печи, страница 2

где K_p – коэффициент пропорциональности;

K_i – коэффициент интегрирования.

Пусть АФЧХ замкнутой системы имеет два комплексных корня характеристического уравнения Р₁ и Р₂, которые находятся в непосредственной близости от мнимой оси координат.

Эти корни и будут определять в основном всю динамику переходного процесса Р_1,2 = -a ± jb. При оценке качества систем управления на основе косвенных методов была получена зависимость степени затухания ψ от ближайшего к мнимой оси корня, связанного с параметром m:

,                                                          (3.3)

где m – колебательность системы, которая соответствует отношению, m=a/b .

При m = 0 имеем границу области устойчивости. При расчетах промышленных систем регулирования чаще всего выбирают значение m от 0,22 (ψ = 0,75) до 0,367 (ψ = 0,9). Зададимся ψ = 0,9, тогда m = 0,3665.

Пусть в комплексной плоскости корней характеристического уравнения мнимая ось сдвинута до совпадения с корнем, местоположение которого характеризуется параметром m. Такому смещению мнимой оси соответствует подстановка частотной области

p = -mω ± jω.                                                          (3.4)

Исходя из условия «попадания» одного из корней на мнимую ось можно в соответствии с критерием Найквиста записать

W_p(-mω ± jω)∙W_oб(-mω ± jω) = -1.                                            (3.5)

Из выражения (3.3) можно получить два уравнения:

Re_pRe_oб -Im_pIm_oб = -1;                                                              (3.6)

Re_pIm_oб + Im_pRe_oб = 0,                                                               (3.7)

где Re_p, Re_oб - соответственно действительные части, Im_p, Im_oб - мнимые части расширенных частотных характеристик регулятора и объекта.

Выделим мнимую и действительную часть W_р:

W_р = - K_p - K_i/((j - m) ω) = mK_i/((m²+1) ω) – K_p+jK_i/((m²+1) ω).              (3.8)

Выделим мнимую и действительную часть W_о:

W_о((j-m)ω)) = Re(W_о((j-m)ω)))+ jIm(W_о((j-m)ω))) = Re_о +jIm_о                   (3.9)

Подставим в уравнения (3.6), (3.7)  выражения из (3.8) и (3.9), получим:

(mK_i/((m²+1) ω) – K_p)·Re_о – K_i/((m²+1) ω)·Im_о= –1                           (3.10)

(mK_i/((m²+1) ω) – K_p)·Im_о + K_i/((m²+1) ω)·Re_о = 0                           (3.11)

Из полученной системы уравнений можно выразить коэффициенты K_p и K_i:

K_p = – (Im_о ·m + Re_о)/( Re_о² + Im_о²);                               (3.12)

K_i = – (Im_о ·ω·(m²+1))/( Re_о² + Im_о²).                                       (3.13)

Далее для произвольно заданных значений ω можно найти множество значений K_p и K_i, которые будут обеспечивать желаемую степень затухания переходного процесса. Имея массив коэффициентов, можно ввести дополнительные критерии качества регулирования для нахождения лучшей пары K_p и K_i. Ориентировочно можно выбирать значения из области параметров, когда произведение K_p·K_i стремится к максимуму.

Для расчета регулятора воспользуемся пакетом MATLAB.

В результате выполнения программы получим множество пар настроек, которые обеспечивают желаемую степень затухания переходного процесса ψ = 0,9. Это множество можно представить графически в виде зависимости  K_i = f (K_p), представленной на рисунке 3.4, которая называется линией равной степени затухания.

В результате выполнения программы определяется пара значений K_p и K_i, для которых произведение Kp·Ki максимально. Получили K_p = 14,84; K_i = 0,261(точка помечена на графике знаком «+»).

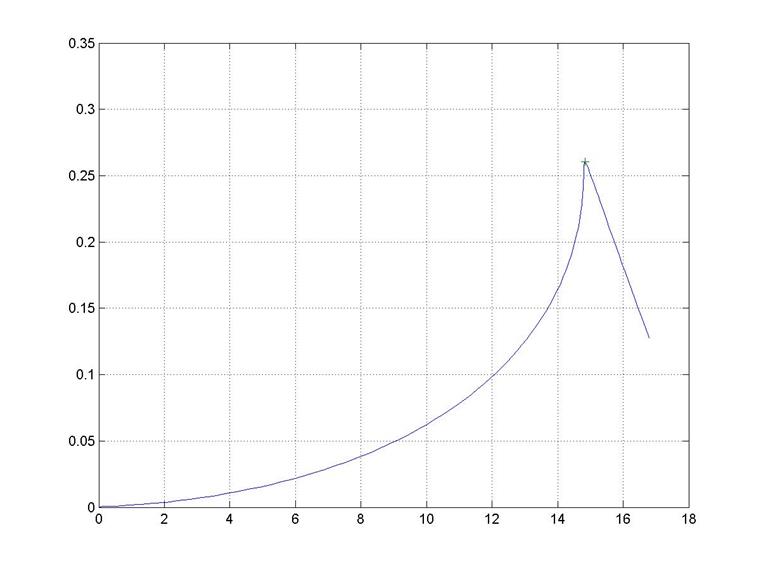
Рисунок 3.4 − Линия равной степени затухания ψ = 0,9 (K_i = f (K_p))

Для моделирования процесса регулирования воспользуемся приложением пакета MATLAB – Simulink. Схема системы регулирования представлена ранее на рисунке 3.3. Первоначально промоделируем систему без учета нелинейностей, для чего исключим из схемы нелинейные элементы. В результате моделирования получим переходную характеристику представленную на рисунке 3.5.  и для регулируемой величины – на рисунке 3.6.

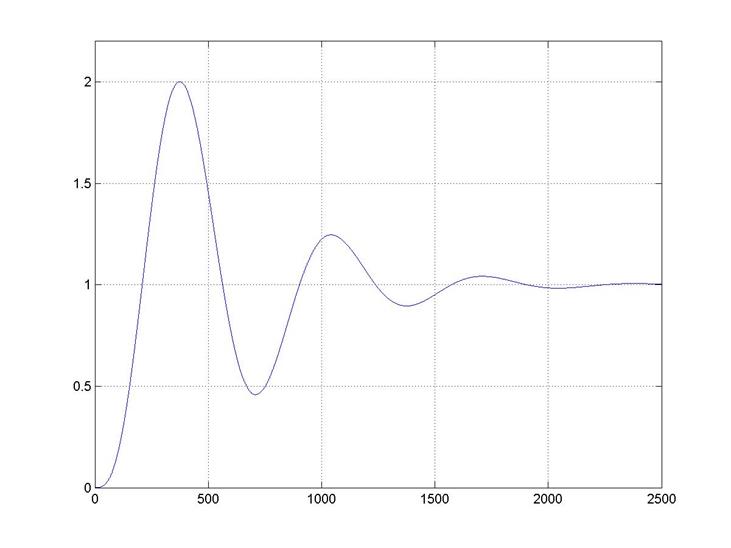
Рисунок 3.5 – Переходная характеристика каскадной системы регулирования (без учета нелинейностей)

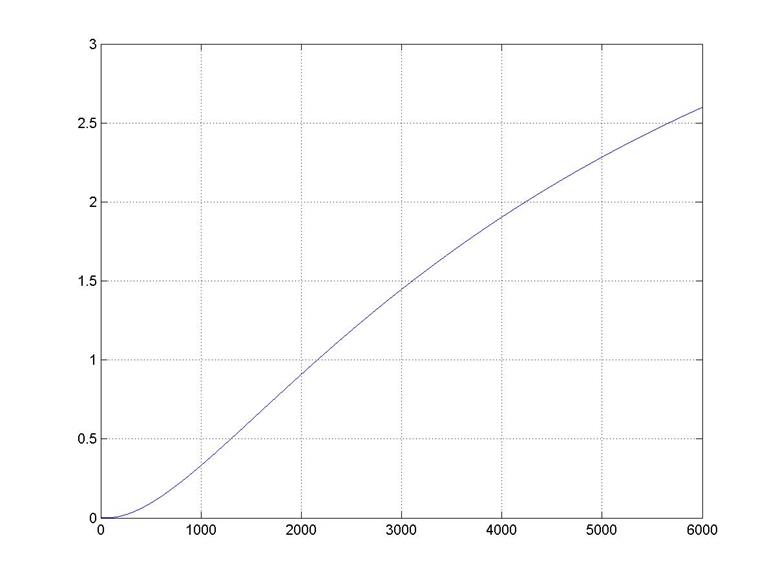
Рисунок 3.6 – Переходная характеристика каскадной системы регулирования (с учетом нелинейностей)

По рисункам 3.5 и 3.6 очевидно, что введение в систему реальных нелинейных элементов, а так же наличие динамической обратной связи (датчика) существенно изменяет качество регулирования. Для получения приемлемой переходной характеристики замкнутой системы введем поправку: будем снижать значения Кп и Ки.

Приемлемый переходный процесс представлен на рисунке 3.7, получен при настройках K_p = 4,5; K_i = 0,0009.

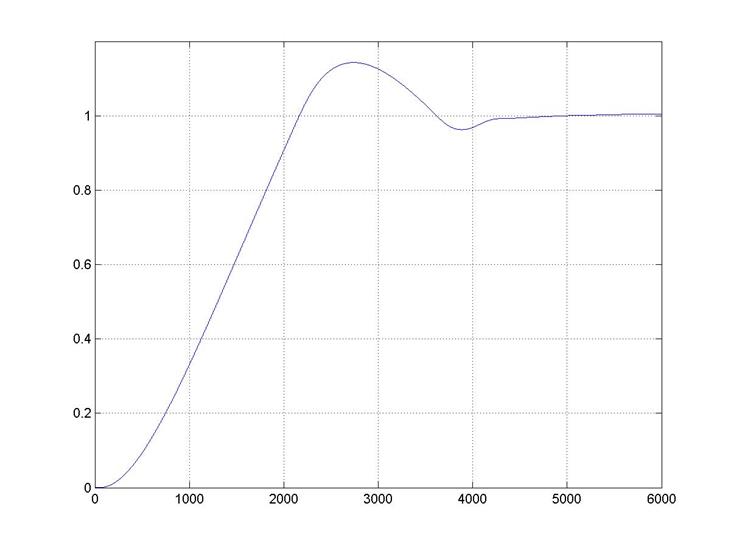
Рисунок 3.7 – Переходная характеристика скорректированной каскадной системы регулирования (с учетом нелинейностей)

Степень затухания переходного процесса:

ψ = (А1 – А2)/А1 = 1.

Перерегулирование:

δ = (h_max/h_уст)·100% = (1,143/1)·100% = 14,3%

Время быстродействия (первое достижение желаемого значения):

t_быстр = 2164 с.

Время регулирования (достижение желаемого значения с допустимой ошибкой 3%):

t_рег = 4018 с.

Измерим сигнал на выходе трехпозиционного релейного элемента (сигнал на закрытие/открытие клапана), представленный на рисунке 3.8; построим график изменения степени открытия клапана от времени, представленный на рисунке 3.9.

В результате моделирования убедились, что каскадная система имеет удовлетворительные показатели качества переходного процесса.

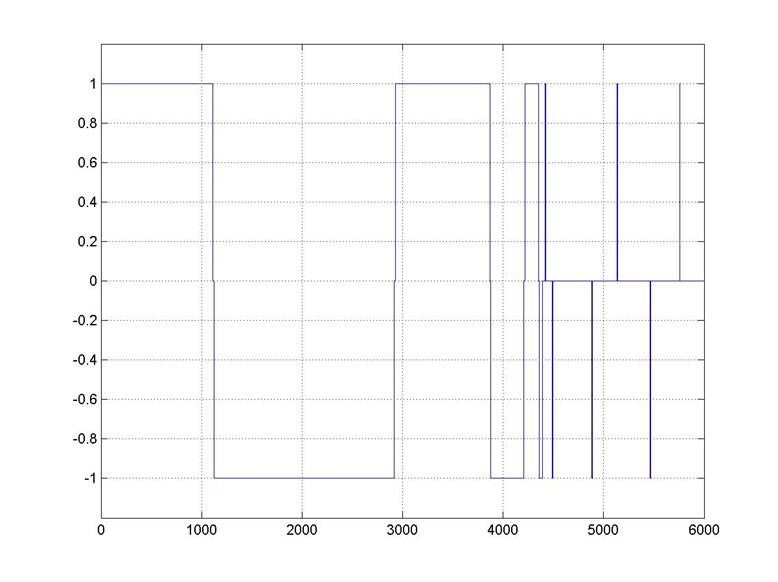
Рисунок 3.8 – Сигнал на выходе трехпозиционного релейного элемента скорректированной каскадной системы регулирования (с учетом нелинейностей)

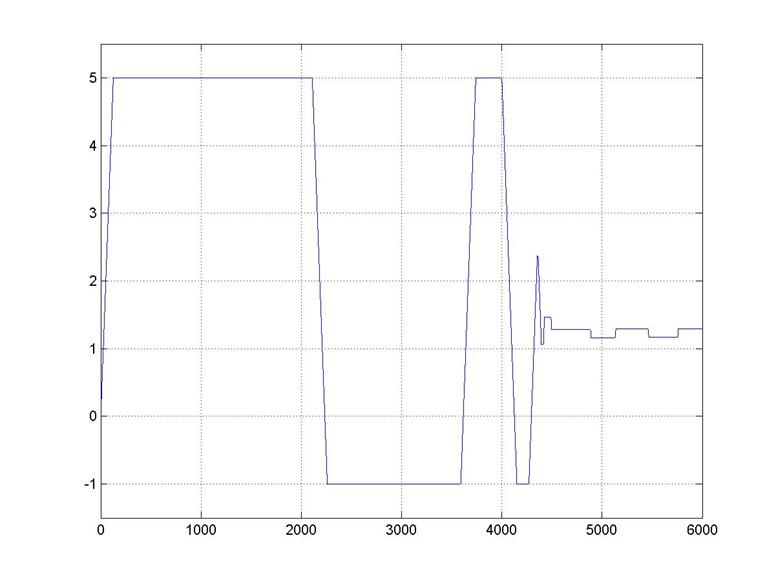
Рисунок 3.9 – Сигнал на выходе исполнительного механизма скорректированной каскадной системы регулирования (с учетом нелинейностей)