






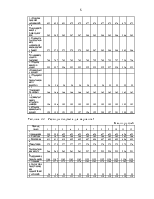
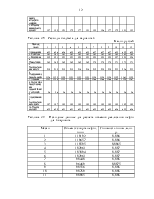

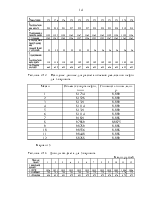

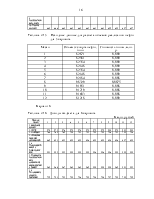
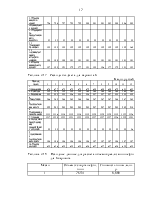



формул, промежуточные вычисление удобно произвести в таблице А.1.
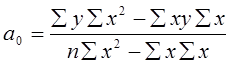 , (1.4)
, (1.4)
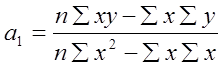 .
(1.5)
.
(1.5)
После составления уравнения для использования полученной модели в последующем анализе, вначале необходимо проверить ее параметры на типичность, что осуществляется по формулам t – критерия Стьюдента (формулы 6 и 7), промежуточные вычисления производятся в таблице А.2.
 , (1.6)
, (1.6)
где ta0 – расчетное значение t - критерия Стьюдента для параметра а0;
n – объем изучаемой совокупности;
se - среднеквадратическое отклонение результативного признака yi от выровненных значений yxi.
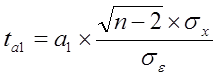 ,
(1.7)
,
(1.7)
где ta1 – расчетное значение t – критерия Стьюдента для параметра а1;
sx – среднеквадратическое отклонение факторного признака xi от среднего x.
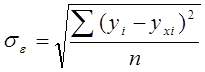 ,
(1.8)
,
(1.8)
где yi – фактическое значение результатирующего признака;
yxi – выровненное значение результатирующего признака (то есть полученное в результате подставки фактического xi в уравнение регрессии).
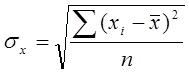 , (1.9)
, (1.9)
где xi – фактическое значение факторного признака (в данном случае объемы реализации нефти в денежном выражении);
![]() - среднее значение факторного
признака.
- среднее значение факторного
признака.
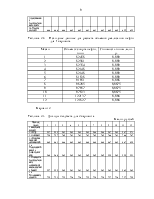
Полученные по формулам 6 и 7 фактические значения ta0, ta1 сравниваются с критическим tk, который определяют по таблице Стьюдента с учетом принятого уровня значимости a (0,05) и числе степеней свободы k (число степеней свободы равно n-2).
Таблица 1.2 – Критические значения t – критерия Стьюдента (для a = 0,05)
|
k |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
|
Значение |
4,303 |
2,776 |
2,447 |
2,306 |
2,228 |
2,179 |
2,145 |
Параметры уравнения признаются значимыми, если ta0 > tk < ta1.
Проверка практической значимости полученной модели осуществляется расчетом индекса корреляции, показывающим тесноту связи между явлениями.
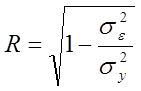 ,
(1.10)
,
(1.10)
где R – индекс корреляции;
s2y – общая дисперсия результативного признака.
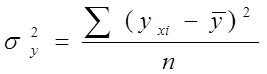 . (1.11)
. (1.11)
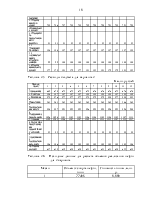
Интерпретация индекса корреляции производится на основе шкалы Чеддока.
Таблица 1.3 – Шкала Чеддока
|
Показания тесноты связи |
0,3 < |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
> 0,9 |
|
Характеристика силы связи |
Слабая |
Умеренная |
Заметная |
Высокая |
Очень высокая |
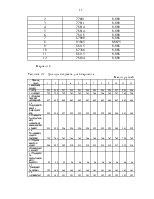
После создания модели характеризующей взаимосвязь между доходами бюджета и объемами реализации нефти, определения ее характеристик, делается прогноз объемов реализации нефти в будущем периоде.
1.6 Произвести прогноз объемов реализации нефти можно лишь в том случае если в пункте 4 было определено присутствие тенденции в реализации нефти.
Для прогнозирования можно использовать кривые роста. Воспользуемся полиномом первой степени yt =b0 + b1x, который на графике выглядит прямой и используется для описания процессов, развивающихся во времени равномерно. Параметры кривой роста можно определить по следующим формулам:
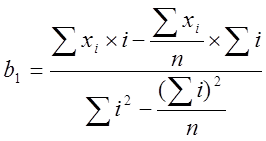 ,
(1.12)
,
(1.12)
где xi – ежемесячный объем реализации нефти в денежном выражении в месяц i;
i – номер месяца.
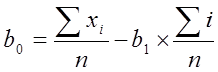 .
(1.13)
.
(1.13)
Точечный прогноз объемов реализации нефти на 1 месяц вперед, с помощью полученной модели, осуществляется подстановкой в нее такого значения i, которое бы соответствовало бы данному сроку прогноза, то есть i = 13 (12 месяцев прошлого года + 1 «прогнозный» месяц).
1.7 Сделайте прогноз доходов бюджета на 1 месяц следующего периода, путем подстановки прогнозных объемов реализации нефти в денежном выражении в регрессионную модель, характеризующую
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.