Определение системных характеристик цепи

МИСТЕРСТВО  РФ ПО СВЯЗИ И ИНФОРМАТИЗАЦИИ

Сибирский государственный университет

телекоммуникаций и информатики

Кафедра ТЭЦ                      

ДОМАШНЯЯ РАБОТА ПО КУРСУ ЦОС

Выполнил:

Студент 3 курса факультета МЭС

Гр. М-84    Горбачев В. А.

Проверил:

Оценка   ___                                             

г.Новосибирск   2000 г.

Определение системных характеристик цепи

Исходные данные:

 а 0 = 0,2;              b1 = -0,6;

а 1 = 0,8;               b 2 = 0,07;

а 2 = - 0,3

 x(nT)={0,4; 0,3; 0,1};

                                                      а0

∑∑

 

                                      T

                       b1                                                       a1

 

                                      T

                      b2                                                         a2

 

Y(z) = X(z)*H(z);

  Часть 1:

а.) Определить передаточную функцию (проверить устойчивость цепи) рассчитать АЧХ,    ФЧХ цепи (с шагом  f 1 = f g /10), построить графики АЧХ, ФЧХ, вычислить h(0Т) по  отcчетам  АЧХ, ФЧХ.

Определение передаточной функции:

                 а 0 +  а 1 z¯¹ + а 2 z¯²          0,2 + 0,8 z¯¹ – 0,3 z¯²

   H(z) =                                      = 

1 -  b1 z¯¹ -  b 2 z¯²          1 + 0,6 z¯¹ - 0,07 z¯²

Найдем нули знаменателя:

 1 + 0,6 z¯¹ - 0,07 z¯² = 0;  =>   z² + 0,6 z¹ - 0,07 = 0 ,

 найдем нули полученной функции:

 z² + 0,6 z¹ - 0,07 = 0;

Д = b²  – 4ac =  0,36 + 0,28 =  0.64;

z12  = -0,6 ±  0.8;

 Определим, попадают  ли корни знаменателя в единичную окружность ( если попадают то, схема устойчива ).

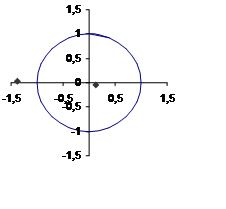Схема устойчива.

а.1) Рассчитаем  АЧХ и ФЧХ цепи, вычислим h(0Т).

- jwT               -  j2πwn

Для этого произведем замену:  z = e     =  e

- j2πwn                 - j4πwn

                  0,2  + 0,8е    – 0,3е

H(jΏ ) =

                                                                        - j2πwn                   - j4πwn

                  1 + 0,6e    - 0,07e

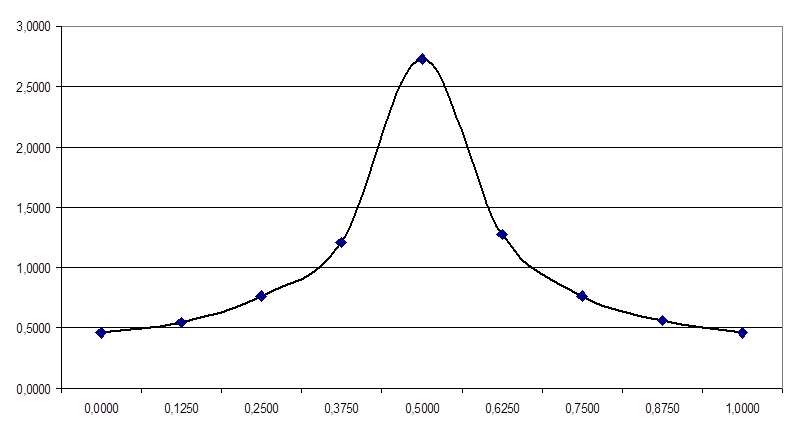
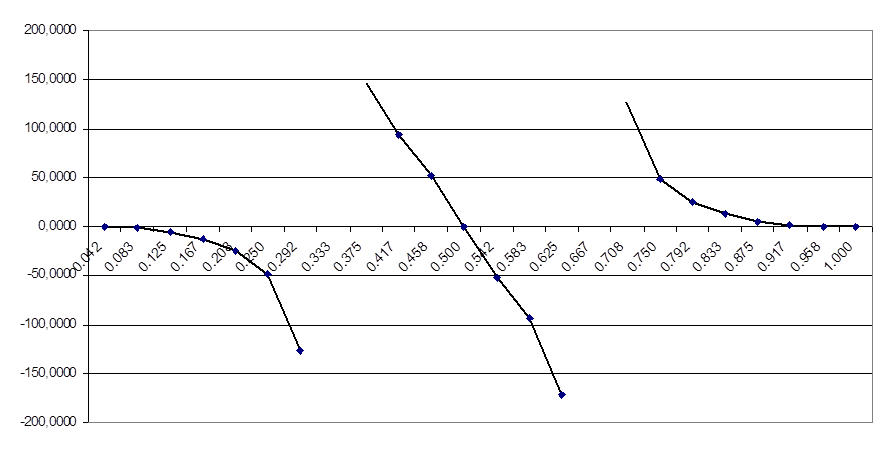
АЧХ и ФЧХ цепи рассчитано програмно (листинг программы предоставлен в приложении ‘А’).

Ώ	|H(Ώ )|	φ
0	0.45752	0
0,125	0.54559	-6.40911
0,25	0.76903	-48.38153
0,375	1.20616	146.14393
0,5	2.72727	0
0,625	1.27288	-171.31171
0,75	0.76903	48.38153
0,875	0.55901	5.10380
1	0,45752	0

                                                              АЧХ

ФЧХ

а.2)

  Расчет h(0T) (по формуле обратного дискретного преобразования Фурье (ОДПФ)):

                    1    8                                       j2πkT/N

h(nT) =        ∑ H(jkw1) e

                   N  k=0

h(0T) = 0.457516+0.554588-0.236911-0.076160+2.727273-0.114305-0.236911+0.208139 +0,45752 = 0.364803

б.) Расчет импульсной характеристики.

б.1)

Расчет импульсной характеристики по передаточной функции.

Передаточная функция имеет вид:

                                                                               - 1                          - 2

                  0,2  + 0,8z– 0,3z

H(z ) =

                                                                        - 1                   - 2

                  1 + 0,6z    - 0,07z

Определим передаточную функцию помощью программы в приложении B:

(для удобства деления вынесем z  в числителе и знаменателе)

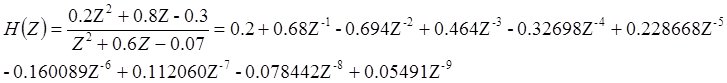
 в результате импульсная характеристика:

 h(nt) ={0.2;0.68;-0.694;0.464;-0.32698;0.228668;-0.160089;0.11206;-0.078442;0.05491};

б.2)

       Расчет импульсной характеристики по разностному уравнению.

                Y(z)

 H(z) =            ;

               X(z)

Y(z)(1 + 0,6z^-1 - 0,07z^-2 ) = X(z)(0,2 + 0,8z^-1  - 0,3z^-2 );

Y(z) = -0,6∙Y(z)∙z^-1 + 0,07∙Y(z)∙z^-2 +0,2∙X(z)+0,8∙X(z)∙z^-1 – 0,3∙X(z)∙z^-2;

Y(z) => Y(nt);

Y(nt) = -0,6∙Y(nt - T) + 0,07∙Y(nt – 2T) +0,2∙X(nt)+0,8∙X(nt - T) – 0,3∙X(nt – 2T) ;

Y(nt) = h(nt);

На вход схемы подаем Δ – функцию ( Δ = {1,0,0,0,0,…}):

Y(nt) =  -0,6∙Y(nt - T) + 0,07∙Y(nt – 2T) + 0,2∙Δ(nt) + 0,8∙Δ(nt - T) – 0,3∙Δ(nt – 2T);

(так как на входе Δ – функция, то только Δ(0Т) = 1, а Δ(-Т), Δ(-2Т),… = 0)

n = 0;

Y(0t) = -0,6 Y(0t – T) + 0,07 Y(0t – 2T) + 0,2∙Δ(0t) + 0,8∙Δ(0t – T) – 0,3∙Δ(0t – 2T) =

       -0,6 Y( – T) + 0,07 Y(– 2T) + 0,2∙Δ(0) + 0,8∙Δ( – T) – 0,3∙Δ( – 2T) = 0,2;

0,2 – получили соответствие;

n = 1;

Y(1t) = -0,6 Y(1t – T) + 0,07 Y(1t – 2T) + 0,2∙Δ(1t) + 0,8∙Δ(1t – T) – 0,3∙Δ(1t – 2T) =

       -0,6 Y( 0 T) + 0,07 Y(– 1T) + 0,2∙Δ(1t) + 0,8∙Δ( 0T) – 0,3∙Δ( – 1T) = 0,68;

получили соответствие;

n = 2;

Y(2t) = -0.6Y(2t – T) + 0,07 Y(2t – 2T) + 0,2∙Δ(2t) + 0,8∙Δ(2t – T) – 0,3∙Δ(2t – 2T) = -0.694

получили соответствие;

n = 3;

Y(3t) = -0.6Y(3t – T) + 0,07 Y(3t – 2T) + 0,2∙Δ(3t) + 0,8∙Δ(3t – T) – 0,3∙Δ(3t – 2T) = 0.464

получили соответствие;

n = 4;

Y(4t) = -0.6Y(4t – T) + 0,07 Y(4t – 2T) + 0,2∙Δ(4t) + 0,8∙Δ(4t – T) – 0,3∙Δ(4t – 2T) = 0,32698

получили соответствие;

n = 5;

Y(5t) = -0.6Y(5t – T) +0,07 Y(5t – 2T) + 0,2∙Δ(5t) + 0,8∙Δ(5t – T) – 0,3∙Δ(5t – 2T) =0.22868

получили соответствие;

n = 6;

Y(6t) = -0.6Y(6t – T) +0,07 Y(6t – 2T) + 0,2∙Δ(6t) + 0,8∙Δ(6t – T) – 0,3∙Δ(6t – 2T) = ;-0.160089

получили соответствие;

n = 7;

Y(7t) = 0,05 Y(7t – T) – 0,2 Y(7t – 2T) + 0,8∙Δ(7t) + 0,6∙Δ(7t – T) – 0,4∙Δ(7t – 2T) = 0.11206;

получили соответствие;

На основании проверки делаем вывод о правильности расчета импульсной характеристики.

Часть 2:

а.) Определить сигнал на выходе цепи.

Исходные данные:

Сигнал на входе:

  x(nt) = {0,4;0,3;0,1};

Импульсная характеристика:

 h(nt) ={0.2;0.68;-0.694;0.464;-0.32698;0.228668;-0.160089;0.11206;-0.078442;0.05491};

Передаточная функция:

                                                                             - 1                          - 2

                  0,2  + 0,8z– 0,3z

H(z ) =

                                                                        - 1                            - 2

                  1 +   0.6z    - 0,07z

а.1)

       По разностному уравнению.

Сигнал на входе:

x(nt) = {0,4;0,3;0,1};

Y(nt) = -0,6∙Y(nt - T) + 0,07∙Y(nt – 2T) +0,2∙X(nt)+0,8∙X(nt - T) – 0,3∙X(nt – 2T) ;

n = 0:

n = 0;

Y(0t) = -0,6 Y(0t – T) + 0,07 Y(0t – 2T) + 0,2∙X(0t) + 0,8∙X(0t – T) – 0,3∙X(0t – 2T) =

       -0,6 Y( – T) + 0,07 Y(– 2T) + 0,2∙X(0) + 0,8∙X( – T) – 0,3∙X( – 2T) = 0.08;

n = 1;

Y(1t) = -0,6 Y(1t – T) + 0,07 Y(1t – 2T) + 0,2∙X(1t) + 0,8∙X(1t – T) – 0,3∙X(1t – 2T) =

       -0,6 Y( 0 T) + 0,07 Y(– 1T) + 0,2∙X(1t) + 0,8∙X( 0T) – 0,3∙X( – 1T) = 0.332;

n = 2;

Y(2t) = -0.6Y(2t – T) + 0,07 Y(2t – 2T) + 0,2∙X(2t) + 0,8∙X(2t – T) – 0,3∙X(2t – 2T) = -0.0536

получили соответствие;

n = 3;

Y(3t) = -0.6Y(3t – T) + 0,07 Y(3t – 2T) + 0,2∙X(3t) + 0,8∙X(3t – T) – 0,3∙X(3t – 2T) = 0.154

получили соответствие;

n = 4;

Y(4t) = -0.6Y(4t – T) + 0,07 Y(4t – 2T) + 0,2∙X(4t) + 0,8∙X(4t – T) – 0,3∙X(4t – 2T) = 0,32698

n = 5;

Y(5t) = -0.6Y(5t – T) +0,07 Y(5t – 2T) + 0,2∙X(5t) + 0,8∙X(5t – T) – 0,3∙X(5t – 2T) =-0.06699

n = 6;

Y(6t) = -0.6Y(6t – T) +0,07 Y(6t – 2T) + 0,2∙X(6t) + 0,8∙X(6t – T) – 0,3∙X(6t – 2T) = 0.063

n = 7;

Y(7t) = -0.6Y(7t – T) + 0,07 Y(7t – 2T) + 0,2∙X(7t) + 0,8∙X(7t – T) – 0,3∙X(7t – 2T) = -0.04254

а.2)

       По формуле свертки (линейной и круговой).

 Импульсная характеристика:

h(nt) ={0.2;0.68;-0.694;0.464;-0.32698;0.228668;-0.160089;0.11206;-0.078442;0.05491};

     а.2.1)

       Линейная свертка:

n

      Y(nt) =  ∑ X(kt)h(nt - kT);  (ф-ла линейной свертки)

                                           k=0

n = 0:

Y(0t) = X(0T)·h(0t-0T) = 0.4*0.2 = 0,08;

n = 1:

Y(1t) = X(0T)·h(1t-0T) + X(1T)·h(1t-1T) = 0,4*0.68+ 0,3*0,2= 0.332;

n = 2:

Y(2t) = X(0T)·h(2t-0T) + X(1T)·h(2t-1T) + X(2T)·h(2t-2T) = -0.4*0.694+0.3*0.68+0.1*0.2=-0.0536;;

n = 3:

Y(3t) = X(0T)·h(3t-0T) + X(1T)·h(3t-1T) + X(2T)·h(3t-2T) +  X(3T)·h(3t-3T) =

   = 0.4*0.464-0.3*0.694+0.1*0.68=0.0454;

n = 4:

Y(4t) = X(0T)·h(4t-0T) + X(1T)·h(4t-1T) + X(2T)·h(4t-2T)  = -0.4*0.32698+0.3*0.464-0.1*0.694=-0.060992

Так как входной сигнал состоит из 3-х значений то (X(3T) = X(4T) = X(4T) = … =  0 и далее, эти значения при расчете по ф-ле линейной свертки я буду опускать).

n = 5:

Y(5t) = X(0T)·h(5t-0T) + X(1T)·h(5t-1T) + X(2T)·h(5t-2T)  = 0.4*0.228668-0.3*0.32698+0.1*0.464=0.03977;

n = 6:

Y(6t) = X(0T)·h(6t-0T) + X(1T)·h(6t-1T) + X(2T)·h(6t-2T)  = -0.4*0.160089+0.3*0.228668-0.1*0.32698=0. 00281332;

n = 7:

Y(7t) = X(0T)·h(7t-0T) + X(1T)·h(7t-1T) + X(2T)·h(7t-2T)  = 0.4*0.11206-0.3*0.160089+0.1*0.228668=0.0036573;

Сигнал на выходе: {0,08;0.332; -0.0536; 0.0454; -0.060992; 0.03977; 0.00281332; 0.0036573}

а.2.2)

Круговая свертка:

N1 = 10; N2 = 3; N = N1 + N2 – 1 = 12;

h(nt) ={0.2;0.68;-0.694;0.464;-0.32698;0.228668;-0.160089;0.11206;-0.078442;0.05491};

Где N1 – число отчетов импульсной характеристики, N2 – число отчетов входного воздействия.

N-1

      Y(nt) =  ∑ X(kt)h(nt - kT);  (ф-ла круговой свертки)

                                           k=0

n = 0:

Y(0t) = X(0T)h(0t – 0T) + X(1T)h(0t – 1T) + X(2T)h(0t – 2T) = 0.4*0.2=0.08;

n = 1:

Y(1t) = X(0T)h(1t – 0T) + X(1T)h(1t – 1T) + X(2T)h(1t – 2T) = 0.4*0.68+0.3*0.2=0.332;

n = 2:

Y(2t) = X(0T)h(2t – 0T) + X(1T)h(2t – 1T) + X(2T)h(2t – 2T)= -0.4*0.694+0.3*0.68+0.1*0.2=-0.0536;

n = 3:

Y(3t) = X(0T)h(3t – 0T) + X(1T)h(3t – 1T) + X(2T)h(3t – 2T) =0.4*0.464-0.3*0.694+0.1*0.68=0.0454;

n = 4:

Y(4t) = X(0T)h(4t – 0T) + X(1T)h(4t – 1T) + X(2T)h(4t – 2T) = = -0.4*0.32698+0.3*0.464-0.1*0.694=-0.060992;

n = 5:

Y(5t) = X(0T)h(5t – 0T) + X(1T)h(5t – 1T) + X(2T)h(5t – 2T) = = 0.4*0.228668-0.3*0.32698+0.1*0.464=0.03977;

n = 6:

Y(6t) = X(0T)h(6t – 0T) + X(1T)h(6t – 1T) + X(2T)h(6t – 2T) = -0.4*0.160089 + 0.3*0.228668 - 0.1*0.32698=0.0028133;

n = 7:

Y(7t) = X(0T)h(7t – 0T) + X(1T)h(7t – 1T) + X(2T)h(7t – 2T) =0.4*0.11206-0.3*0.160089+0.1*0.228668=0.0036573;

Сигнал на выходе: {0,08;0.332; -0.0536; 0.0454; -0.060992; 0.03977; 0.00281332; 0.0036573}

а.3)

       По Z – изображению сигнала на выходе цепи.

                               ∞                         -n                                          -1                  -2

 X(z) =  ∑ X(nt)z = 0,4 + 0,3z +0,1z ;

                             n=0

Y(z) = H(z)X(z);

                                                                                - 1                        - 2                                           - 1                     - 2

                  (0,2  + 0,8z– 0,3z  )( 0,4 + 0,3z + 0,1z )

   Y(z ) =

                                                                                                                       - 1                         - 2

                                       1 + 0.6  z   - 0,07z

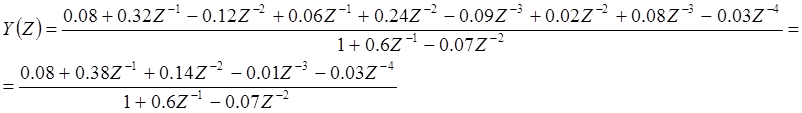
Далее делим помощью программы Полином числитель на знаменатель:

Получаем: 0.08+0.332Z^-1-0.0536 Z^-2+0.0454 Z^-3-0.060992 Z^-4+0.039773 Z^-5-

-0.028133Z^-6+0.00365 Z^-7-0.013768 Z^-8+0.009637 Z^-9

Сигнал на выходе: {0,08;0.332; -0.0536; 0.0454; -0.060992; 0.03977; 0.00281332; 0.0036573}

Часть 3:

 Определить разрядность коэффициентов аi , bi , если допуск на отклонение системы характеристик составляет 1%;

Разрядность = 9;

Перевод в двоичную систему производим с помощью программы в приложении C

а0 = 0,2;

а0 = 0 0 1 1 0 0 1 1 0 0  +  1 =0 0 1 1 0 0 1 1 0

а0 =0.19921875;

а1 = 0,8;

а1 = 1 1 0 0 1 1 0 0 1 1  + 1 = 1 1 0 0 1 1 0 1 0

а1 =0.79980469;

а2 = -0,3;

а2 =  0 1 0 0 1 1 0 0 1 1  +  1  =  0 1 0 0 1 1 0 1 0

а2 = -0.29980469

b1 = -0,6;

b1 = 1 0 0 1 1 0 0 1 1 0   +  1  = 1 0 0 1 1 0 0 1 1

b1 = -0.59960938;

b2 = 0,07;

b2 = 0 0 0 1 0 0 0 1 1 1   +  1 = 0 0 0 1 0 0 1 0 0

b2 = 0.06933594

Записываем импульсную характеристику с новыми аi, bi. Получаем новую

Импульсную характкристику.

                                                hi’ - hi

Далее рассчитываем δi =               ·100% , для каждого hi (где hi’ и hi  соответственно

            hi’

   значения “новой” импульсной характеристики и “ старой ” ).

∞             δi²

Далее, если  δ = ∑                       > 1 , то увеличиваем разрядность на 1 и делаем все

i=0              i

   сначала.

Часть 4:

 Рассчитать энергию шума квантования на выходе цепи, полагая АЦП = 9;

а.) Определяем шаг квантования:

    ΔАЦП = 1/512 = 0,001953125;

    Δумножителя = 1/1024 = 0.00097656;

b.) Строим шумовую модель: источники шума 4-ре умножителя и АЦП.

λ 0,2

∑∑

 

                                                 T

                                -0,6 0,8

 

                                                  T

                                0,07-0,3

 

с.) Чтобы вычислить дисперсию шума необходимо знать дисперсию источника.

Расчет ведем методом округления:

Δ²АЦП

σ0 =              =  0,001953125²/12 = 3.17·10^-7  – энергия шума от АЦП;

          12

                         Δ²умножителя

σ1 = σ2 = σ3 =                 = 7.9·10^-9  энергия шума от 1-го умножителя;

                            12

 Строим импульсную характеристику от выходов источников шума