Изучение методов определения весовых функций разомкнутой системы автоматического управления

Балтийский Государственный Технический Университет

им    Д.Ф.Устинова

                                                «Военмех»

                                                 Кафедра А5

                              Лабораторная работа №1

   Определение весовых функций разомкнутой САУ.

                               Вариант №23

                                                                                 Выполнил: Щербаков

                                                                                             Алексей, А482

                                                                                  Проверил: Санников

                                                                         Виталий Андреевич

                                       Санкт-Петербург, 2012

Цель работы: изучение методов определения весовых функций разомкнутой системы автоматического управления (САУ)

Основными характеристиками линейных стационарных динамических систем  являются весовые функции и частотные характеристики. С помощью этих показателей могут решаться задачи анализа устойчивости и точности САУ при неслучайных и случайных воздействиях, а также задачи синтеза САУ.

Весовой функцией, или импульсной переходной функцией динамической системы, имеющей один вход и один выход, называется реакция системы в момент t  на единичный импульс, действующей на систему в момент τ.

                                 δ(t-τ)                                             q(t,τ)

 

                                                   q(t,τ)=A_tδ(t,τ)

                        где

  q(t,τ) – весовая функция,

  A_t – оператор динамической системы, преобразующий функцию времени  t   на входе системы в реакцию системы,

δ(t-τ) -  импульсная δ-функцией называется функция, равная нулю всюду, кроме начала координат, принимающая бесконечное значение в начале координат, такая, что интеграл от нее по любому интервалу интегрирования, содержащему начало координат, равен единице:

                                                                δ(t)=0, если t≠0                                      1.1

                                                                δ(0)=∞

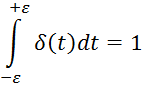
Весовая функция может быть получена моделированием, если на вход системы подать δ-функцию.  Импульсное воздействие и весовая функция, рассматриваемые  как функции текущего времени t при фиксированном значении τ=τ₁, представлены на рис.1.2. Весовая функция отвечает условию физической  возможности: q(t,τ)=0 при t<τ. Это условие отражает тот факт, что любая физическая система может реагировать в момент t только на воздействия, приложенные к системе до этого момента времени, т.е. при t >τ. Для стационарных систем весовая функция зависит только от разности аргументов t – τ:

q(t,τ)= q(t-τ). Выбирая момент τ=0, схему моделирования для определения весовой функции стационарной системы можно  представить в виде рис.1.3. многомерная динамическая система, имеющая несколько входов и выходов, характеризуется матрицей весовых функций:

G(t,τ)=[q_ij(t,τ)]

Весовой функцией q_ij(t,τ), соответствующей i-му выходу и j-му входу, называется реакция системы в момент t  на i-м выходе при действии в момент τ импульсного возмущения на j-м входе. 

Весовые функции являются важными характеристиками динамических систем и позволяют определить реакцию системы на произвольные воздействия:

                              X_i(t)=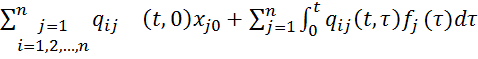

Где x_i – фазовые координаты

X_jo – начальные условия

f_j(0) –входные воздействия.

δ(t-τ )                                                            q(t,τ)

                      δ(t-τ₁)

 

                                                        t                         

               t=τ-τ₁                                                                     t=τ-τ₁

рис.1.2

                                       δ(t)                                                     q(t)

 

                                     (τ=0)

                                                        Рис.1.3.

                                Описание работы и исходные данные

Рассмотрим систему стабилизации углового движения ЛА относительно ц.м. в продольной плоскости. В качестве программного движения принимается полет ЛА на заданной высоте с постоянной скоростью. Принимается, что динамика системы стабилизации описывается линейными дифференциальными уравнениями в отклонениях относительно программного движения.

1) 

2) 

3)  =

4) 

где  – угол атаки, - угол тангажа, - угловая скорость тангажа, -угол отклонения руля высоты,  – известные динамические коэффициенты, i₁,i₂ – передаточные числа, -известная функция, задающая программу угла тангажа.

в системе уравнений индекс  отклонений от программных значений опущен. Уравнения 1)-3) описывают динамику ЛА, уравнение 4) – уравнение системы управления. При этои рулевая машина считается безынерционной.

Системе уравнений соответствует структурная схема системы стабилизации угла тангажа.

                                                                                                                            

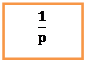
                    Передаточная функция ЛА, характеризующая передачу воздействия от входа

до выхода  , имеет вид

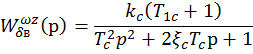
Где

 – коэффициент усиления ЛА

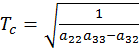 – постоянная времени ЛА

 – коэффициент демпфирования

 – постоянная времени форсирующего звена.

Для получения передаточной функции необходимо применить преобразования Лапласа к системе и решить полученную систему алгебраических уравнений.

Численные значения коэффициентов.

Исходные данные:

вариант
23	-1.7	-3.8	-1.4	3.6	1.8	0.35

Задача 1.1

Определение весовых функций разомкнутой САУ.

Динамика углового движения неуправляемого ЛА описывается следующими уравнениями:

=

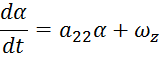
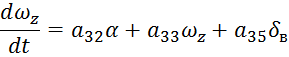
Входным воздействием является отклонение руля высоты

Выходными величинами -

Система характеризуется весовыми функциями

                                                                

                                                                 

Которые определяются моделированием, если на вход системы вместо  подать  – функцию.

На основании свойства   – функции, определяемого соотношением 1.1, можно заменить воздействие в виде  – функции начальными условиями. Тогда весовые функции определяются моделированием однородной системы:

                   

=

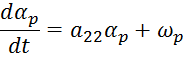
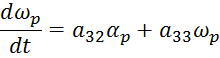
C начальными условиями

                                                                

                                                                 

Таким образом для определения весовых функций

           

                                                                

                                                                  (t)

Соответствующих разомкнутой системе, необходимо выполнить моделирование системы с начальными условиям. Моделирование осуществляется с помощью пакета Matlab, система дифференциальных уравнений решается методом Рунге-Кутта с постоянным шагом.

Интегрирование от t=0 до t=ТК=10 секунд

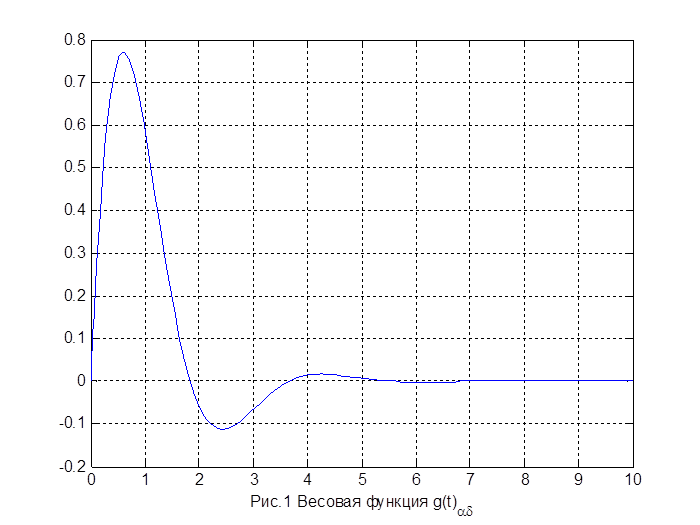
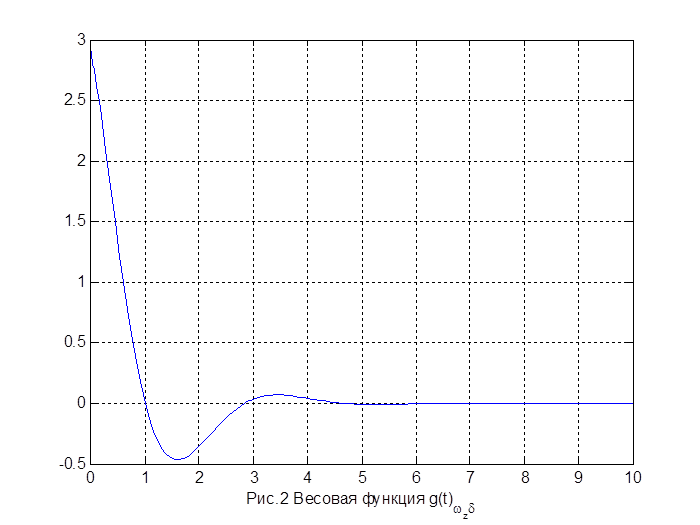
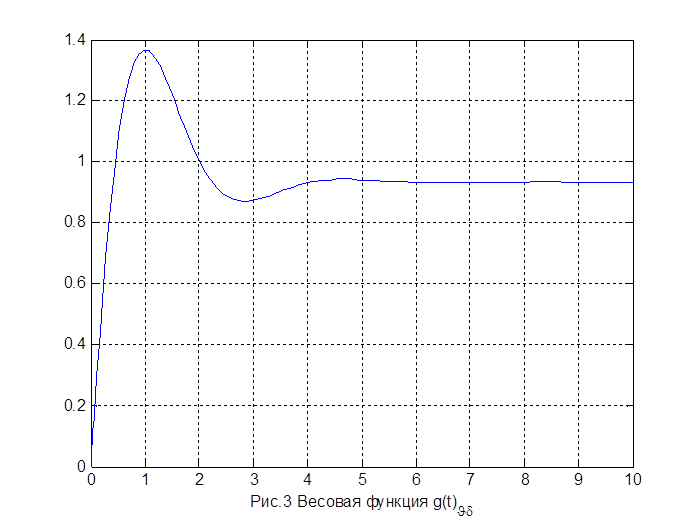
Таблица 1.2

t	alpha	wz	teta
0.00000	0.00000	2.90000	0.00000
0.43989	0.72966	1.51441	0.98768
1.07405	0.52796	-0.11828	1.36328
1.54740	0.15678	-0.46487	1.19917
2.09253	-0.08088	-0.31124	0.97326
2.52314	-0.11075	-0.10535	0.88483
3.09391	-0.05462	0.04900	0.87685
3.54252	-0.00864	0.06661	0.90532
4.08074	0.01521	0.03411	0.93348
4.52270	0.01459	0.00624	0.94199
5.09481	0.00514	-0.00932	0.93998
5.54030	-0.00035	-0.00870	0.93571
6.05941	-0.00239	-0.00347	0.93251
6.52017	-0.00177	0.00010	0.93182
7.07274	-0.00043	0.00145	0.93238
7.43479	0.00012	0.00119	0.93287
8.49646	0.00021	-0.00011	0.93336
8.61724	0.00016	-0.00016	0.93334
9.10287	0.00001	-0.00020	0.93324
9.60664	-0.00005	-0.00010	0.93316
10.00000	-0.00005	-0.00002	0.93314

Листинг программы

Файл lab1_1.m

function dy = lab1_1(t,y)

dy = zeros(3,1);

a22 = -1.7;

a32 = -3.8;

a33 = -1.4;

a35 = 3.6;

dy(1) = a22* y(1) + y(2);

dy(2) = a32* y(1) + a33 * y(2);

dy(3) = y(2);

Файл lab1.m

[T Y] = ode45(@lab1_1, [0 10], [0 2.9 0]);

dlmwrite('myfile1.txt', [T Y], 'delimiter', '\t', 'precision', '%10.5f', 'newline', 'pc');

plot(T, Y(:,1));

xlabel('Рис.1 Весовая функция {g(t)_{\alpha\delta}}');

grid on;

figure;

plot(T, Y(:,2));

xlabel('Рис.2 Весовая функция {g(t)_{{\omega_z}\delta}}');

grid on;

figure;

plot(T, Y(:,3));

xlabel('Рис.3 Весовая функция {g(t)_{\vartheta\delta}}');

grid on;