Проектирование стального каркаса пятиэтажного здания в г. Березники, имеющего размеры в плане 27*42 м, страница 2

где k – поправочный коэффициент для стен с проемами; ; A_n – площадь нетто по горизонтальному сечению стены; A_b – площадь стены брутто; k_р – поправочный коэффициент для столбов, который принимается равным в зависимости от величины h_red

Значение величины h_red определяется по формуле:

, где i – радиус инерции сечения стены в осях.

Определим радиус инерции сечения стены. Для этого вначале определим положение центра тяжести сечения стены.

Рисунок 4 – Схема простенка

- определим статический момент и площадь сечения (рис. 4): мм2 Откуда положение центра тяжести сечения будет равно:

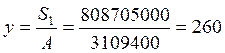мм

Определим момент инерции сечения относительно центральной оси:

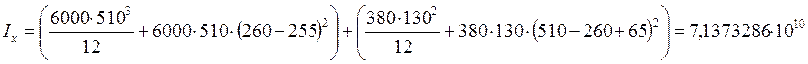Откуда радиус инерции будет равен:

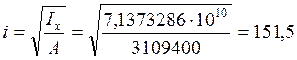мм

Следовательно: мм. Откуда отношение высоты стены к ее толщине будет равно:

Определим значение поправочного коэффициента k для этого необходимо определить площадь сечения нетто  мм²,откуда 

, следовательно

Толщина стены удовлетворяет условию предельной гибкости.

3.2 Проверка прочности простенка

При расчете прочности простенка будем учитывать, что нагрузки от карниза, покрытия и верхних этажей прилаживаются в центре тяжести сечения стены, а нагрузку от перекрытия, опирающегося на стены рассматриваемого этажа, учитывают приложенной с фактическим эксцентриситетом.

С учетом ранее определенных нагрузок вычислим продольную силу в рассматриваемом сечении:

кН

Определим положение центра тяжести сечения простенка (рис 5): м3 -площадь простенка будет равна:  м2 получим: м

Рисунок 5 – Сечение простенка

Рисунок 6 – Схема приложения вертикальной нагрузки

Определим изгибающий момент, который определяется по формуле: кН∙м. определим момент в рассматриваемом сечении, который вычислим через подобие треугольников: кН∙м Определим эксцентриситет e0: м Определим момент инерции относительно главной центральной оси:

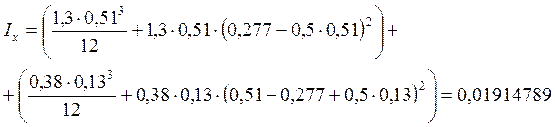
Определим радиус инерции: 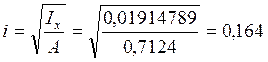   м так как i=0,164>0,087, то m_g=1

При жестких опорах и сборных железобетонных перекрытиях расчетная длинна сжатого элемента определяется по формуле:

м

Гибкость всего элемента определим по формуле:

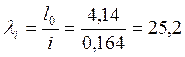
По таблицам 15 и 18 СНиПа II-22-81 определяем: упругая характеристика кладки α=1000, откуда интерполяцией определяем коэффициент продольного изгиба φ

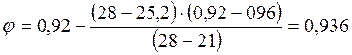
Определим площадь сжатой части сечения:

м

Вычислим расстояние от точки приложения силы до края полки сжатой части сечения

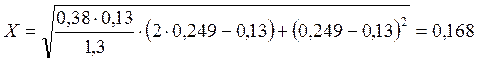, высота сжатой части сечения будет равна: м

Площадь сжатой части сечения равна:

м

Определим центр тяжести сжатой части сечения:

м³, откуда

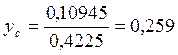м

Определим радиус инерции сжатой части сечения:

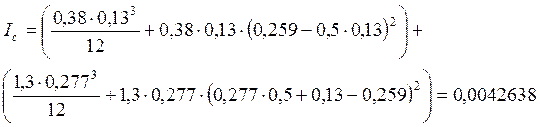
получим: м

Определим гибкость 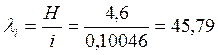, откуда

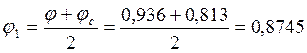
Определим коэффициент ω:

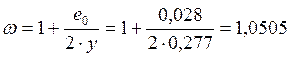
Расчетная несущая способность простенка N_cc будет равна:

кН

прочность простенка не обеспечена.

Проверим необходимость расчета по раскрытию трещин: 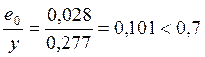, поэтому расчет по раскрытию трещин не производим.

Так как прочность простенка не обеспечена, поэтому увеличим марку раствора до 50 и произведем перерасчет несущей способности простенка:

кН, прочность кладки не обеспечена, поэтому необходимо выполнить армирование данного простенки для обеспечения его прочности.

3.3 Расчет сетчатого армирования простенка

В соответствии со СНиП II-22-81 «Каменные и армокаменные конструкции» расчет внецентренно сжатых элементов с сетчатым армированием при малых эксцентриситетах, не выходящих за пределы ядра сечения следует производить по формуле:

, где

 - расчетное сопротивление армированной кладки при внецентренном сжатии, определяемое при марке раствора 50 и выше по формуле:

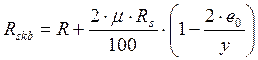, здесь

μ – процент армирования кладки сетчатой арматурой, который определяем по таблицам в зависимости от диаметра арматурных стержней и размера ячейки сетки.

R_s(f_cd) – расчетное сопротивление арматурной стали, принимаем арматуру S 240 с R_s=218МПа