Строительство и архитектура \ Железобетонные конструкции

Проектирование трехэтажного промышленного здания (высота этажа – 5 м, район строительства – г. Вологда)

Страницы работы

34 страницы (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

Скрытые стыки можно осуществить с подрезкой торца ригеля и опиранием его на железобетонную или металлическую консоль колонны высотой, не превышающей высоту подрезки. Такие стыки применяют для общественных зданий. Стыки с подрезкой ригеля проектируются для восприятия небольших нагрузок. Они также обладают меньшей жесткостью по сравнению со стыками без подрезки ригеля.

2. Плита перекрытия

Плиты опираются свободно одним концом на ригель, другим – на ригель или стену. Расчетный пролет принимаем равным расстоянию между центрами опорных площадок – 6м. Нагрузки, складывающиеся из постоянных и временных, в том числе из кратковременно и длительно действующих, сведем в таблицу 1.

Таблица 1 Нагрузки на плиту перекрытия

№	Нагрузки, кПа	Нормат.	γf	Расчёт.
	Постоянные
1	Пол	0,50	1,2	0,60
2	Плита перекрытия	3,00	1,1	3,30
	Итого	3,50		3,90
	Временные
3	Стационарное оборудование	2,00	1,2	2,40
4	Вес людей и материалов	5,00	1,2	6,00
	Итого	7,00		8,40
	Суммарные
5	Полные	10,50		12,30
6	В т.ч. длительные	5,50		6,30

3. Расчет ригеля

3.1. Нагрузки

Таблица 2 Подбор сечения ригеля

№	Наименование	Формула	Расчёт
1	Расчетная призменная прочность бетона для В20, МПа	R_b=	11,5
2	Полная суммарная нагрузка, кПа	g_п=	12,30
3	Длина ригеля, м	L_р=	5,8
4	Полная нагрузка на ригель, кПа	g=L_рg_п	71,34
5	Расчетный изгибающий момент для свободно опертой балки наибольшего из пролетов без учета нагрузки от ее собственного веса, кНм²	М=(L_р²g)/8	299,98
6	Рабочая высота, м	h_o=1,85(M/R_b)^1/2	0,549
7	Высота сечения, м	h=h_o+0,05	0,599
8	Ширина сечения, м	b=h_o/2,4	0,229
9	Принимаем, м	h_o	0,60
10	Принимаем, м	b	0,25

Таблица 3 Нагрузки, действующие на ригель

№	Нагрузки	Нормат.	γf	Расчёт.
	Постоянные
1	Пол	2,90	1,2	3,48
2	Плита перекрытия	17,40	1,1	19,14
3	Ригель 25х60 см	3,75	1,1	4,13
	Итого	24,05		26,75
	Временные
3	Стационарное оборудование	11,60	1,2	13,92
4	Вес людей и материалов	29,00	1,2	34,80
	Итого	40,60		48,72
	Суммарные
5	Полные	64,65		75,47
6	В т.ч. длительные	35,65		40,67

Таблица 4 Подбор коэффициента φ_b₂

№	Наименование	Формула	Расчёт
1	Отношение, суммарной длительной нагрузки к суммарной полной	q_l/q	0,539
2	Коэффициент	φ_b2=0,9/(q_l/q)	1,67
3	Допустимое значение коэффициента	φ_b2	1,1
4	Принято	φ_b2	1,1

3.2. Подбор продольной арматуры и расчет несущей способности ригеля.

Арматура подбирается для всех пролетов и опор по максимальным пролетным и опорным изгибающим моментам с учетом их перераспределения и симметрии конструкции. Опорная арматура в связи с выравниванием моментов может быть одинаковой для всех опор.

h=	0,60	м
b=	0,25	м
Класс бетона	В25
φ_b2=	1,1
R_b=1,1*11,5	12,65	МПа
Арматура класса	А-II
R_sc=R_s=	280	МПа

Таблица 5

№	Формулы и обозначения		Пролеты			Опоры
			1	2		В	С
			+	+	-	-	-
	Подбор арматуры
1.1.	М, кНм		197	145	59	197	172
1.2.	h_o,м		0,55	0,55		0,55	0,55
1.3.	В_о=М/R_bbh_o²		0,206	0,152		0,206	0,180
1.4.	ξ=1-(1-2В_о)^1/2		0,233	0,165		0,233	0,200
1.5.	А_s=R_bbξh_o/R_s,см		14,48	10,26		14,48	12,41
	Сечение
	Состав	количество	2	2	2	2	2
		диаметр, мм	22	18	22	22	20
		количество	2	2		2	2
		диаметр, мм	22	18		22	20
		площадь	7,60	5,09	7,60	7,60	6,28
		площадь	7,60	5,09		7,60	6,28
	Площадь		15,20	10,17	7,60	15,20	12,56
	Расчет несущей способности при необорванных стержнях
2.1.	А_s,см2		15,20	10,17	7,60	15,20	12,56
2.2.	А_s',см2			7,60
2.3.	а=ΣА_isa_i/A_s, см		5,65	5,05	3,30	3,30	3,00
2.4.	h_o=h-a,м		0,544	0,550	0,567	0,567	0,570
2.5.	a' ,м			0,0033
2.6.	ξ=(R_sA_s-R_scA_s')/R_bbh_o		0,248	0,041	0,119	0,237	0,195
2.7.	2а'/h_o			0,012
2.8.	В_о=ξ(1 - 2ξ)		0,217		0,112	0,209	0,176
2.9.1.	М=B_oR_bbh_o²+ R_scA_s'(h_o-a'),кНм		202,6		113,5	212,6	180,9
2.9.1.	М=RsAs'(ho-a'),кНм			155,6
	Выполняется М<М_расчет		ДА	ДА	ДА	ДА	ДА
	При двух оборваных стержнях
2.10.	А_s,см2		7,60	5,09		7,60	6,28
2.11.	А_s',см2
2.12.	а, см		3,30	2,90		3,30	3,00
2.13.	h_o=h-a,м		0,567	0,571		0,567	0,570
2.14.	ξ=(R_sA_s-R_scA_s')/R_bbh_o		0,119	0,079		0,119	0,098
2.15.	Во=ξ(1-2ξ)		0,112	0,076		0,112	0,093
2.16.1.	М=B_oR_bbh_o²+ R_scA_s'(h_o-a'),кНм		113,5	78,1		113,5	95,3
2.16.2.	М=R_sA_s'(h_o-a'),кНм

3.3. Подбор поперечной арматуры

При расчете поперечной арматуры обычно задаются диаметром поперечных стержней, который из условия сварки связан с диаметром продольных стержней (при одностороннем расположении стержней – 0,25 диаметра продольного стержня, при двустороннем расположении – 0,5).

При назначенном диаметре поперечных стержней отыскивается их шаг в для крайних и средних четвертей каждого пролета ригеля

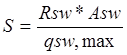
qsw,max – максимальное значение поперечной силы, воспринимаемой поперечными стержнями на единицу длинны элемента.

Исходными данными для расчета служат значения поперечных сил в опорных сечениях и максимальные в средних четвертях пролета.

Принимаем шаг хомутов, который должен быть не более максимального Smax = φ_b4R_btbh_o²/Q.

Соблюдение этого условия предотвращает разрушение по наклонному сечению, проходящему между соседними плоскостями хомутов, по которому вся поперечная сила воспринимается только бетоном.

Прочность поперечного сечения по наклонной полосе между наклонными трещинами зависит от интенсивности поперечного армирования, размеров сечения и прочности бетона на сжатие.

1 пролета h_o=	0,54	м	2 пролета h_o=		0,55	м
2h_o=	1,09	м		2h_o=	1,10	м
b=	0,25	м
Класс бетона	В25		E_s=	2,10E+05
R_b=1,1*11,5=	12,65	МПа	E_b=	2,40E+04
R_bt=1,1*1,05=	1,155	МПа	φ_b2=	2
Арматура класса	А-I		φ_b3=	0,6
R_sw=	225	МПа	φ_b4=	1,5
Число ветвей	2
φ_n=φ_f=	0

Таблица 6 Подбор поперечной арматуры вригеле и расчет его несущей способности по поперечной силе

№	Формула или обозначение	Четверти I пролета			Четверти II пролета
№	Формула или обозначение	Левая	Правая	Средние	Левая	Правая	Средние
	Обоснование необходимости расчета
1.1.	Q,кН	189	253		224	219
1.2.	Q(3L/4)=(3Q_пр-Q_л)/4			142,5			108,25
1.3.	φ_b3R_btbh_o, кН	94,2	94,2	94,2	94,2	94,2	94,2
1.4.	Q<>φ_b3R_btbh_o	>	>	>	>	>	>
	Подбор поперечной арматуры
2.1.	φ_b2R_btbh_o², кН		170,6			174,7
2.2.	g_sw=Q²/(4φ_b2R_btbh_o²), кН/м	52,35	93,81	29,76	71,81	68,64	16,77
2.3.	Со=(φ_b2R_btbh_o²/q_sw)^1/2	1,81	1,35	2,39	1,56	1,60	3,23
2.4.	C_o<>2h_o	<	<	>	<	<	>
2.5.	q_sw=0,5Q/2h_o ,кН/м	86,94	116,38	65,55	101,82	99,55	49,20
2.6.	qsw=φ_b3R_btb/2 ,кН/м	86,6	86,6	86,6	86,6	86,6	86,6
2.7.	d_sw ,мм	12	12	12	10	10	10
2.8.	A_sw=2πd_sw2 /4 ,см²	2,26	2,26	2,26	1,57	1,57	1,57
2.9.	S=R_swA_sw/q_sw,_max ,м	0,585	0,437	0,587	0,347	0,355	0,408
2.10.	S_max=φ_b4R_btbh_o/Q , м	0,677	0,506	0,898	0,585	0,598	1,210
2.11.	S<h/3 и S<500 мм	0,200	0,200		0,200	0,200
	S<0,75h			0,450			0,450
2.12.	Принято S, мм	200	200	450	200	200	450
	Проверка прочности
3.1.	q_sw=R_swA_sw/S,кН/м	254,3	254,3	113,0	176,6	176,6	78,5
3.2.	С_о=φ_b2R_btbh_o²/q_sw	0,819	0,819	1,228	0,995	0,995	1,492
3.3.	C_o<>2h_o
3.4.1.	Q_wb = 2(φ_b2R_btbh_oq_sw)^1/2 ,кН	417	417		351	351
3.4.2.	Q_wb= 2h_oq_sw+φ_b2R_btbh_o²/C_o ,кН			262			203
3.5.	Q<>Qwb	<	<	<	<	<	<
	Проверка достаточности бетонного сечения
4.1.	φ_b1=1-0,01R_b		0,874			0,874
4.2.	μ_sw100=(A_sw/bs)*100	0,45	0,45	0,20	0,31	0,31	0,14
4.3.	α= E_s/E_b		8,75			8,75
4.4.	φ_w1=1+ 5αμ_sw	1,20	1,20	1,09	1,14	1,14	1,06
4.5.	Q_c=0,3R_bbh_oφ_b1φ_w1	540	540	490	518	518	484
4.6.	Q<>Qc	<	<	<	<	<	<

3.4.Обрыв продольных стержней

Различают теоретическое и практическое места обрыва стержней. Теоретическое находиться в сечении где обрываемый стержень не нужен по эпюре моментов. Для этого используют результаты расчетов несущей способности при двух оборванных стержнях. Расстояние от теоретического обрыва до практического определяется по формуле

Таблица 7 Расчет обрыва продольных стержней

№	Формула или обозначение	Арматура первого пролета				Арматура второго пролета
		Пролетная		Опорная		Пролетная		Опорная
		Слева	Справа	I гр	II гр	Слева	Справа	Слева	Справа
1	М, кНм	113,5	113,5	-113,5	0	78,1	78,1	-113,5	-95,3
2	Загружение	1	1	2	2	2	3	1	1
3	q=g, кН/м			26,75	26,75			26,75	26,75
4	M_sup,l, кНм			1,0	0,0			172,0	172,0
5	M_sup,r, кНм			172,0	172,0			172,0	172,0
6	q=g+p ,кН/м	75,47	75,47			75,47	75,47
7	M_sup,l, кНм	0	0			172,0	197,0
8	M_sup,r, кНм	172,0	172,0			172,0	165,0
9	b=0,5l+(M_sup,l - M_sup,r)/ql ,м	2,51	2,51	1,80	1,79	2,90	2,97	2,90	2,90
10	C=2(M+M_sup,l)/q ,м2	3,01	3,01	-8,41	0,00	6,63	7,29	4,38	5,73
11	X_1:2=b+(b²-C)^1/2,м	0,70	4,32	5,21	3,58	1,57	4,22	4,91	4,54
12	Q_1:2=0,5q(1-2X_1:2)+(M_sup,l - M_sup,r)/l,кН	136,62	-136,62	-91,26	-47,91	100,72	-93,89	-53,72	-43,76
12	Q_1:2=0,5q(1-2X_1:2)+(M_sup,l - M_sup,r)/l,кН	136,62	-136,62	-91,26	-47,91	100,72	-93,89	-53,72	-43,76
13	Сечение A_sw : состав
	арматура класса	А-I	А-I	А-I	А-I	А-I	А-I	А-I	А-I
	диаметр, мм	12	12	12	12	10	10	10	10
	площадь, см²	2,26	2,26	2,26	2,26	2,26	2,26	2,26	2,26
14	S, м	0,45	0,45	0,2	0,2	0,45	0,45	0,2	0,2
15	q_sw = R_sA_sw/S ,кН/м	140,7	140,7	316,5	316,5	140,7	140,7	316,5	316,5
16	d, мм	22	22	22	20	18	18	20	20
17	W >Q_1:2/2q_sw + 5d ,м	0,596	0,596	0,254	0,176	0,448	0,424	0,185	0,169
18	W>20d ,м	0,44	0,44	0,44	0,4	0,36	0,36	0,4	0,4
19	>	440	440	250	170	360	360	180	160

3.5. Расчет деформаций

Прогиб определяем в первом пролете при невыгодном загружении. Поэтому прежде всего вычисляются изгибающие моменты от нормативных нагрузок для оплрного и пролетного сечений.Для расчета необходимо вычисление величины Wpl – момента сопротивления сечения с учетом пластических деформаций. Эта величина подсчитывается для пролетного и опорного сечений.

Таблица 8 Пролетный и опорный моменты в первом пролете от полных и длительных нагрузок при невыгодном для пролета загружении

№	Загружение			Сечение
индекс	схема			Пролетное		Опорное
индекс	схема				М, кН		М, кН
1	Полные нагрузки
310		q_n=	24,1	0,080	202,67	0,100	149,19
320		p_n=	40,6	0,101	202,67	0,050	149,19
2	Длительные
310		q_nl=	24,1	0,080	104,14	0,100	100,42
320		p_nl=	11,6	0,101	104,14	0,050	100,42

b=	0,25	м
В пролете h_о=	0,544	м	E_s=	2,10E+05		МПа
На опоре h_o=	0,567	м	E_b=	2,40E+04		МПа
R_b,ser=	18,5	Мпа
R_bt,ser=	1,6	Мпа	α=	E_s/E_b	8,75
Арматура опорная A_s=	15,20	см2	b=	0,9
Пролетная A_s=	15,20	см2

Таблица 9 Расчет кривизн в опорном и пролетном сечениях ригеля

Информация о работе

ВУЗ:

Белорусский государственный университет транспорта (БелГУТ)

Предмет:

Железобетонные конструкции

Тип:

Курсовые работы

Категория:

Строительство и архитектура (Технические предметы)

Размер файла:

2 Mb

Скачали:

Скачать файл

Проектирование трехэтажного промышленного здания (высота этажа – 5 м, район строительства – г. Вологда)

Страницы работы

Фрагмент текста работы

Похожие материалы

Информация о работе