Сдвиг
Если на гранях элемента действуют только касательные напряжение то такой вид напряженного состояния называется чистым сдвигом. Примером тела во всех точках которого имеет место чистый сдвиг является скручиваемый стержень круглого поперечного сечения. На практике деформацию чистого сдвига можно осущистьвить при кручении тонкостенной трубы.Перемещение какого либо сечения в его плоскости относительно другого параллельного ему сечения называется сдвигом. На сдвиг работают сварные и заклепочные соединения
Закон Гука при чистом сдвиге.
γ-относительная угловая деформация или угол сдвига (ввиду её малой величины tgγ=Δ/a=γ
Для многих материалов при нагружении до пределов пропорциональности пи сдвиге между напряжениями и деформациями сохраняется линейная зависимость - з. Гука при сдвиге.
γ = τ /G (G-модуль упругости 2го рода (модуль сдвига) τ = γ* G. Он характеризует способность материалов сопротивляться деформации сдвига. По анологии з. Гука при растяжении величина линейного перемещения при сдвиге определяется по формуле.
Δ= (Q*a)/(GA)
GA-жесткость при сдвиге.
Линейная зависимость между касательными напряжениями и деформациями сохраняются до тех пор пока τ не преобретут величины предела пропорциональности. Между модулем упругости Е и модулем сдвига G и коэффициентом Пуассона μ существует зависимость
G=E/2(1+ μ)
Сложное сопротивление
Это такой вид деформации, при котором в поперечном сечении стержня возникает не менее 2х внутренних усилий. Исключение плоский изгиб так как в расчетах на прочность при изгибе учитываются только изгибающий момент.
Порядок расчета задач на сложное сопротивление.
В начале используя метод сечений определим внутренние усилия
возникающие в поперечном сечении стержней (при сложной нагрузке рекомендуется
строить эпюры внутренних усилий и определить опасные точки сечения. Затем на
основании принципа суперпозиции определяем напряжения возникшие от каждого
внутреннего усилия отдельно. Для этого используем ранее выведенные формулы σ=
; σ=M*y/I; σmax=Mmax/W) Исследуя
распркделение напряжений по высоте сечения для этого строим эпюры напряжения
устанавливаем опасную или предположительно опасную точкусечения для которой и
составляем условие прочности. Если напряженное состояние в опасной точке
является двуостным то в расчетах используем 3 и 4 теории прочности.
Косой изгиб
Определение напряжений
Косым изгибом называется такой изгиб груза когдаплоскость действия изгибающего момента в данном сечении не совпадает ни с одной из главных осей инерции. В этом случае возникающий изгибающий момент можно разложить на 2а изгибающих момента действующих в плоскостях проходящие через главные оси инерции. То есть диф-ю косого изгиба можно првести к изибу в двух плоскостях.
На балку действует сила перпендикулярная продольной оси и составляющая сосью у некоторый угол φ.
Разложим силы на составляющие Fy=F*cos φ; Fz=F*sin φ.На расстоянии х от свободного конца балки рассмотрим сечение 1234. Mz=Fy*x; My=Fz*x. Используя принцип независимости действия сил определим в указанном сечении в произвольной точке А напряжение, возникшее действием силы F.
σ= σz+ σy=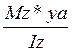
+ 
=
+
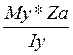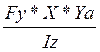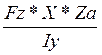(Ya и Za координаты точки А)
Используем верхние формулы. =F*X(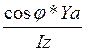
+
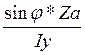). Эта формула для определения
нормальных напряжений при косом изгибе в сечении где возникает изгибающий
моментдля точки А.В общем виде формула имеет вид.
σ=+/-М(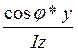
+
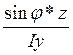) (1). Знак «-» «+» принимается
исходя из физического смысла + растягивание, - сжимание.
Рассмотрим выделенное сечение 1234 и используя ф-лу 1 определим напряжение в условных точках.
σ=Mz*Ymax/Iz+ My*Zmax/Iy = Mz/Wz+My/Wy (2)
σ1= Mz/Wz-My/Wy; σ2= Mz/Wz+My/Wy= σmax; σ3= -Mz/Wz+My/Wy;
σ4= -Mz/Wz-My/Wy= σmin.
Определение положение нейтральной оси при косом изгибе.
Нейтральная линия образуется пересечением нейрального слоя с
плоскостью поперечного сечения σно=0 так как M=F*l не равно 0
то выражение в скобках (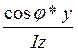+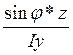)=0
YHO=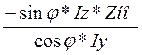
=-tgφ*Iz*Zно/Iy
tgα=-Уно/ Zно; -Zно* tgα= Уно; tgα=tgφ*Iz/Iy
В случае косого изгиба нейтральная линия не перпендикулярна линии действия силы. Положение нейтральной оси определяется углом φ и отношением Iz/Iy. Если Iz=Iy
Уно= -Zно* tgα. => в сечениях типа круг квадрат и крольцо диф-я косого изгиба не возникает.
Условие прочности при косом изгибе.
Для проверки прочности при косом изгибе необходимо
установить опасное сечение, тоесть сечение где М=Мmax
и для точек наиболее удаленных от нейтральной оси используя формулу определения
напряжения σmax=Мmax(+)≤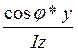
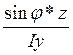[σ] (3)
В случае если материал одинаково работает на растяжение и сжатие.
Для этого составляют два уравнения прочности.Для того чтобы установить опасные точки сечения необходимо провести касательные к сечению параллельно нейтральной оси точки касания и есть опасные точки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.