Математика \ Дискретная математика

Множества и операции над ними. Соответствия и функции, отношения, страница 2

Тема №2  Соответствия  и  функции, отношения.

Любое подмножество rÍА´В декартового произведения множеств называется соответствием из множества А в множество В. Другими словами: если данному ХÎА сопоставлены несколько YÎB (образов Х при соотношении), то говорят, что задано соответствие из множества А в множество В. Обозначим его r.

Пример №1:          Обратные тригонометрические функции сопоставляющие  х ÎR множество таких у, что  х=sin(у).

Для упорядоченных пар, связанных соответствием r будем писать (х;у)Îr.

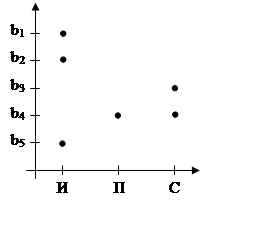
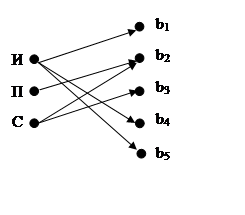
Пример №2: рассмотрим множество программистов А={И;П;С}и множество программ В={b1,b2,b3,b4,b5}. Зададим соответствие r из А в В, связывающее программиста и разрабатываемую им программу.

r={(И;b1);(И;b4);(И;b5);(П;b2);(С;b2);(С;b3)}

Графиком соответствияr из множества А в В назовем Сr множество пар (х,у), где х и у связаны соответствием r , т.е  у Îr(х) ( r (х) не элемент В, а его подмножество!). Указанное множество Сr упорядоченных пар есть подмножество А´В.                     СrÍ А´В.

 


Рисунок     График и и граф отношения для примера №2.

При r совпадающим со всем А´В его называют универсальным соответствием.

Область определения соответствияrÍ А´В  -  это множество первых компонент упорядоченных пар.       D(r)={х:ú$ уÎB  (х;у)Îr }.

Область значения соответствия rÍ А´В. - это множество вторых компонент упорядоченных пар.       R(r) = {у: ú$ х ÎA, (х;у) Îr}.

Из определения следует, что         D(r) ÍA,            R(r) ÍB.

Соотношение называется всюду определённым, если         D(r) = А.

Сечением соответствияrÍ А´В              для фиксированного элемента Х Î А называется такое множество r(х)={у ½(х;у) Îr} или иными словами  r(х) – множество всех “образов ” элемента х  при данном соответствии.

Сечением соответствия r по множеству С Í А будем называть множество:  r(C) = {у ê(х;у) Îr , х ÎC}.

Пример: (про программистов):    

 область определения - rÍ А´В   D(r) = А

 область значения - rÍ А´В равна В;

сечения по элементам:     r(П)={b2}r(И)={b1,b4,b5}r(C)={b2;b3}.

Сечение по множеству:  Х={И;П}r(Х) = {b1,b2,b4,b5}.

Соответствие rÍ А´А из множества А в себя , т.е. подмножество множества А2 называют бинарным отношением на  А  и обозначается:

аr b := (a,b) ÎrÌA´A .

Соответствие rÍ А´В называется бинарным  отношением на А и В.

n-арным или n-местным отношением  на множествах А1,…,An  называется произвольное подмножество r декартового произведения A1´A2´ ….´An  (множество всех упорядоченных кортежей).

Пример №3: Простейший пример бинарного отношения на R´Rэто X<Y,или и т.п. отношения сравнения.

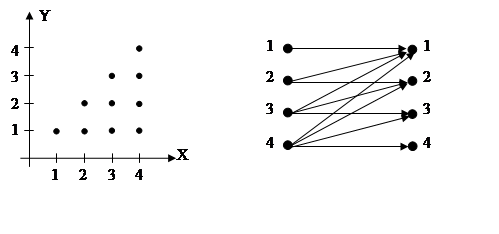
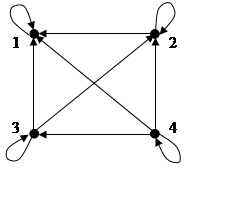
Пример №4:.Пусть А = {1,2,3,4}XrY : = X³YÌA´A.  Тогда

r = {(1;1);(2;2);(2;1);(3;3);(3;2);(3;1);(4;4);(4;3);(4;2);(4;1)}

область определения  .D(r) = {1,2,3,4}.

область значения.R(r) = {1,2,3,4}.

 


Рисунок  График и и граф отношения для примера №4.

Пример №5: Множество точек окружности  - есть график бинарного отношения .

Пример №6: Пусть задано универсальное множество U. Тогда отношение Î есть отношение из U  в булеан 2U. А отношения Ì и = есть отношения на булеане 2U.

Пусть r - бинарное отношение на А. Введём следующие понятия:

-  Обратное отношение

-  Дополнение отношения

-  Тождественное отношение

-  Универсальное отношение (универсальное соответствие)

Композицией отношений (слово бинарные далее будем подразумевать)  и  называется отношение  определяемое следующим образом: .

Композиция отношений на множестве А, есть отношение на множестве А.

n
 
Степенью отношения  называется его композиция с самим собой.

Ядром отношения r из А в В называется композиция .

Ядро отношения r из А в В является отношением на А.

Примеры:

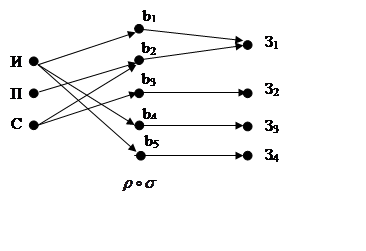
  1. Пусть задано М и |M|=n. Рассмотрим отношение r из 2М в множество целых неотрицательных чисел {0,…,n}. . , тогда ядром отношения r будет отношение равномощности.
  2. Рассмотрим в условиях примера про программистов. Þ отношение s из {b1…b5} в множество заказчиков {З1, З2, З3, З4}.

Композицию этих отношений рассмотрим на примере графа.

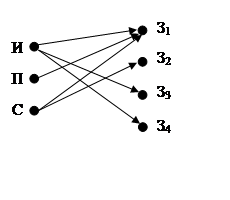
Тогда можно изобразить на одном графе

 


Сечением композиции отношений по элементу И.

              и

Свойства отношений

Пусть  тогда отношение ρ называется:

- рефлексивным если для  ;

- антирефлексивным если для  ;

- симметричным если для  ;

- антисимметричным если для  если из ;

- транзитивным если для  если из ;

- полным или линейным если для  из .

Теорема А: Пусть  есть отношение не А, тогда оно:

1)  рефлексивно,

2)  симметрично,

3)  транзитивно,

4)  антисимметрично,

5)  антирефлексивно,

6)  полно,

Доказательство:

1)рефлексивно значит для  

  .

2)симметрично если для ( из )  ()() ()  

 (&)

( для ) из определения обратного отношения. И т.д.

Отношения эквивалентности

 - это отношение обладающие свойствами рефлексивности, симметричности и транзитивности. Обозначается º:

               Пример:

  1. Отношение равенства чисел или множеств
  2. Отношение равномощности множеств
  3. Отношение параллельности двух прямых или плоскостей в Евклидовой геометрии.

Подмножество элементов множества М, эквивалентных х, называется классом эквивалентности [x]º :={y | y э М & у ºх}

ЛЕММА № 1             Для любого a э М [a]º ¹ 0           

Доказательство: т. к. a º a следовательно a є[a]º . Лемма доказана.

ЕММА №2    а º b следовательно [a]º = [b]º

               Доказательство: Если а º b, то для любого х є [a]º  выполняется условие x º a и а º b следовательно  x º b и  x є [b]º  или если любой      х є [b]º  следовательно x º b, а т. к. b º a, то х º а и значит x є [a]º . Т. е. [a]º = [b]º .

               ЛЕММА № 3   a º b => [a] Ç [b] = Æ

               Доказательство: (от противного ) Пусть [a] Ç [b] ¹ 0 следовательно существует x є [a] Ç [b], т. е. х є [a] и  х є [b]значит x º a и х º b, значит а º b, получили противоречие.   Итак a º b

               ТЕОРЕМА.  Всякое отношение эквивалентности на множестве М определяет разбиение множества М, не содержащие пустых элементов; и наоборот. Разбиение множества М, не содержащее Æ, определяет отношение эквивалентности на М.

               Если R – отношение эквивалентности на М, то множество классов эквивалентности называется фактормножеством множества М по эквивалентности R.:                M/R: = {[x]R}xєм

Фактормножество является подмножеством Булеана. 2м

               Пример № 1. Пусть R – отношение эквивалентности на С.  Z1 R Z2 , тогда если |Z1| = |Z2|, то С/R-множество концентрических окружностей, включая вырожденные.

Отношения порядка

Антисимметричное, транзитивное отношение называется отношение порядка. Позволяет сравнивать между собой различные элементы одного множества.

Рефлексивное отношение порядка - нестрогого порядка ;

антирефлексмивное отношение порядка  - строгого порядка ;

полное отношение порядка - полного порядка<;

не обладает полнотой - отношение частичного порядка.

Множество М, на котором введено отношение порядка, называется упорядоченным.

Пример1.    Отношение< на множестве чисел является отношением строгого порядка и следовательно, множество чисел упорядочено линейно.

Пример2.    Отношение  на булеане 2М - есть отношение нестрогого частичного порядка следовательно булеан – это частично упорядоченное множество.

Элемент х множества М с отношением порядка < называется минимальным, если не существует меньших элементов.              Ø$ yM  y<x & y¹x.

Пример3     .Пустое множество есть минимальный элемент булеана по включению.

ТЕОРЕМА Во всяком конечном, непустом, частично упорядоченном множестве существует минимальный элемент.

ТЕОРЕМА  Всякий частичный порядок можно на конечном множестве дополнить до полного порядка.

Скачать файл