Анализ параметров электропотребления. Статистический анализ вариационных рядов. Корреляционный анализ: двухмерная модель

Совокупность является однородной, если коэффициент вариации не превышает 33%.

Для исследования распределения случайной величины достаточно ограничится вычислением моментов наблюденного ряда распределения не выше четвертого порядка включительно.

Для удобства вычисления произведений составляется таблица:

Таблица2.1

Первый начальный момент

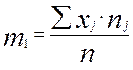            (2.10)

Второй начальный момент

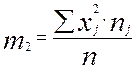           (2.11)

Третий начальный момент

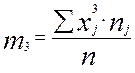            (2.12)

Четвертый начальный момент

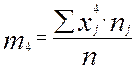           (2.13)

Центральные моменты вычисляются по формулам

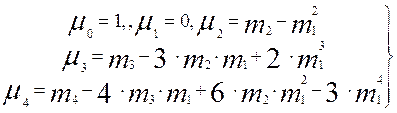        (2.14)

Где второй центральный момент – дисперсия ряда, а квадратный корень из дисперсии – основное отклонение:

 ;             (2.15)

Основные моменты определяются по формулам

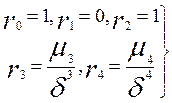              (2.16)

Третий основной момент служит для определения показателя асимметрии – А_с, а разность между четвертым основным моментом и числом 3 служит для определения показателя эксцесса – Е_к кривой распределения.

            (2.17)

 (2.18)

Величина асимметрии может быть положительной и отрицательной. Положительная величина показателя асимметрии указывает на наличие правосторонней асимметрии, а отрицательная – левосторонней асимметрии.

Оценка степени существенности этого показателя дается с помощью средней квадратической ошибки, которая рассчитывается [124] по формуле 2.19.

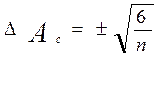             (2.19)

Если отношение 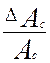< 3, то асимметрия несущественна.

Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. В нормальном распределении эксцесс равен нулю.

Если эксцесс положительный, то распределение островершинное при отрицательном – плосковершинное.

Оценка степени существенности этого показателя дается с помощью средней квадратической ошибки, которая рассчитывается по формуле 2.20:

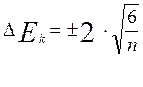              (2.20)

Если отношение 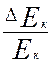 < 3, то эксцесс несущественен.

Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли данное распределение отнести к типу кривых нормального распределения [ 124].

Если непрерывная случайная величина имеет плотность распределения

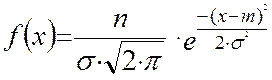               (2.21), то она подчиняется закону нормального распределения. Для построения кривой нормального распределения достаточно знать два параметра: s, х_ср.

Нормальное распределение имеет место в том случае, когда на величину признака влияет большое число случайных причин. Действие этих причин независимо, и ни одна из причин не имеет преобладающего влияния над другими.

Основные свойства кривых оцениваемых нормальным законов распределения изложены ниже [127].

1)  Кривая симметрична относительно максимальной ординаты. Максимальная ордината соответствует значению .

2)  Кривая асимптотически приближается к оси абсцисс, продолжаясь до бесконечности. Следовательно, чем больше значения отклоняются от ,тем реже они встречаются. Одинаковые по абсолютному значению, но противоположные по знаку отклонения значений переменной  от равновероятны.

3)  Кривая имеет две точки перегиба, находящиеся на расстоянии  от .

4)  При с увеличением  кривая становится более пологой. При с изменением кривая не меняет свою форму, а лишь сдвигается вправо и влево по оси абсцисс.

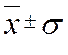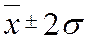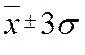5)  В промежутке  находится 68,3% всех значений признака. В промежутке  находится 95,4% всех значений признака. В промежутке  находится 99,7% всех значений признака.

Степень расхождения теоретических и эмпирических частот оценивается на основе особых показателей – критериев согласия, с помощью которых проверяется гипотеза о законе распределения.

Одним из часто употребляемых критериев согласия является критерий “хи-квадрат” (c²), рассчитываемый по формуле 2.22:

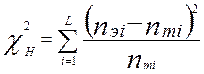              (2.22)

где n_тi – теоретическая частота i-го интервала,

n_эi – эмпирическая частота i-го интервала,

L – число интервалов.

Чем больше разность между наблюдаемыми и теоретическими  частотами, тем больше величина критерия Пирсона. Чтобы отличить существенные значения c² от значений, которые могут возникнуть в результате случайностей выборки, рассчитанное значения критерия сравнивается