Работа выполняется на универсальной
машине УММ-10 или разрывной машине Р-5 (описание машины см. в лаб. раб. №1).
Для измерений деформаций образца применяются рычажные тензометры: ![]() и
и ![]() -
тензометры для измерения продольной деформации;
-
тензометры для измерения продольной деформации; ![]() и
и
![]() - тензометры для измерения
поперечной деформации (рис.4.2).
- тензометры для измерения
поперечной деформации (рис.4.2).
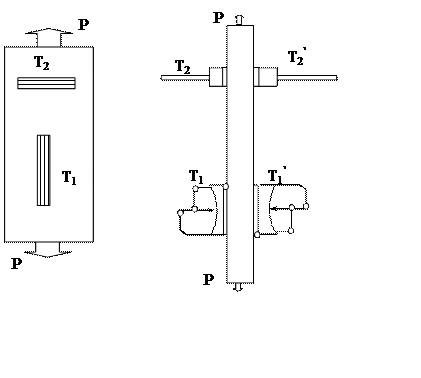
Рис. 4.2. Схема расстановки тензометров на образце.
Указанные деформации определяются как средние из показаний двух тензометров ввиду возможного внецентреннего приложения растягивающей силы и, следовательно, неравномерного распределения напряжений в образце.
1. Нагрузить образец начальной нагрузкой и записать показания тензометров.
2. Давая одинаковые приращения
растягивающего усилия ![]() , произвести четыре – пять
нагружений образца в пределах упругости, записывая каждый раз показания
тензометров.
, произвести четыре – пять
нагружений образца в пределах упругости, записывая каждый раз показания
тензометров.
3. Разгрузить образец.
4. Произвести обработку результатов
опыта: вычислить средние арифметические приращения продольных и поперечных
деформаций (соответственно ![]() и
и ![]() ) при увеличении нагрузки на
) при увеличении нагрузки на ![]() ; рассчитать коэффициент Пуассона.
; рассчитать коэффициент Пуассона.
Коэффициент Пуассона может быть
рассчитан по зависимости 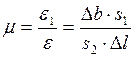 ,
,
где ![]() и
и ![]() базы
тензометров Т1 и Т2 . Если учесть, что базы тензометров
равны между собой (
базы
тензометров Т1 и Т2 . Если учесть, что базы тензометров
равны между собой (![]() ), то величины продольных и
поперечных деформаций будут пропорциональны некоторому постоянный
), то величины продольных и
поперечных деформаций будут пропорциональны некоторому постоянный
коэффициенту ![]() :
:
![]()
где ![]() и
и ![]() -
соответствующие значения сигналов от тензометров. Тогда:
-
соответствующие значения сигналов от тензометров. Тогда:
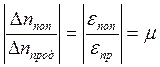 .
.
Результаты измерений и их обработки
представим таблицей 4.1., куда поместим отклонения результатов от среднестатистического
значения ![]() . На основании 19 измерений получим
. На основании 19 измерений получим 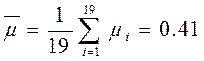
Таблица 4.1.
Результаты эксперимента
|
№ |
Показания тензометров |
Результаты вычислений |
|||
|
|
|
|
|
|
|
|
1 |
0,22 |
0,48 |
0,45 |
0,0361 |
|
|
2 |
0,14 |
0,36 |
0,38 |
0,27 |
0,0729 |
|
3 |
0,15 |
0,34 |
0,44 |
0,26 |
0,0676 |
|
4 |
0,17 |
0,4 |
0,425 |
0,24 |
0,0576 |
|
5 |
0,19 |
0,42 |
0,45 |
0,22 |
0,0484 |
|
6 |
0,2 |
0,5 |
0,4 |
0,21 |
0,0441 |
|
7 |
0,21 |
0,47 |
0,45 |
0,2 |
0,04 |
|
8 |
0,2 |
0,52 |
0,385 |
0,21 |
0,0441 |
|
9 |
0,3 |
0,62 |
0,48 |
0,11 |
0,0121 |
|
10 |
0,23 |
0,54 |
0,426 |
0,18 |
0,0324 |
|
11 |
0,2 |
0,59 |
0,339 |
0,21 |
0,0441 |
|
12 |
0,18 |
0,43 |
0,419 |
0,23 |
0,0529 |
|
13 |
0,17 |
0,44 |
0,386 |
0,24 |
0,0576 |
|
14 |
0,2 |
0,49 |
0,408 |
0,21 |
0,0441 |
|
15 |
0,13 |
0,36 |
0,36 |
0,28 |
0,0784 |
|
16 |
0,28 |
0,72 |
0,88 |
0,13 |
0,0169 |
|
17 |
0,27 |
0,7 |
0,386 |
0,14 |
0,0196 |
|
18 |
0,44 |
1,1 |
0,4 |
-0,03 |
0,0009 |
|
19 |
0,4 |
0,89 |
0,449 |
0,01 |
0,0001 |
Вычислим стандарт отклонения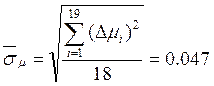 . Задаваясь доверительной
вероятностью
. Задаваясь доверительной
вероятностью ![]() определим коэффициент Стьюдента
определим коэффициент Стьюдента ![]() . При этом граница доверительного
интервала будет
. При этом граница доверительного
интервала будет ![]() .
.
Окончательное значение коэффициента
Пуассона с вероятностью 95% запишем в виде ![]()
Согласно данным [1] коэффициент
Пуассона для латуни изменяется в пределах ![]() .
.
Цель работы – экспериментальное определение величины нормальных напряжений в балке трубчатого сечения при изгибе и проверка результатов опыта теоретическим расчетом.
Работа выполняется на установке
СМ-18А. Напряжения измеряются электротензометрическим способом с помощью
прибора
ИД-70.

Рис. 5.1. Схема установки СМ-18А.
Установка позволяет определить
напряжения в балке 1 трубчатого сечения, защемленной одним концом в станине 2 и
загруженной на другом конце поперечной силой ![]() ,
которая может иметь любое, наперед заданное значение не свыше 10 кгc. Усилие
,
которая может иметь любое, наперед заданное значение не свыше 10 кгc. Усилие ![]() создается посредством
установки грузов 3 на подвес 4. Возникающие при этом напряжения измеряются с
помощью датчиков Т1 и Т 2. Материал образца
(балки) – сплав Д16Т.
создается посредством
установки грузов 3 на подвес 4. Возникающие при этом напряжения измеряются с
помощью датчиков Т1 и Т 2. Материал образца
(балки) – сплав Д16Т.
1. Измерить наружный диаметр трубы ![]() и расстояние
и расстояние ![]() от
сечения приложения нагрузки до сечения, в котором измеряется напряжение.
Внутренний диаметр трубы
от
сечения приложения нагрузки до сечения, в котором измеряется напряжение.
Внутренний диаметр трубы ![]() .
.
2. Подключить измеритель деформаций к датчику Т 1.
3. Приложить к балке начальную
нагрузку ![]() и взять отсчет по реохорду измерительного
прибора
и взять отсчет по реохорду измерительного
прибора ![]() .
.
4. Давая одинаковые приращения
поперечной силы ![]() , произвести три-четыре
нагружения балки, записывая каждый раз отсчеты
, произвести три-четыре
нагружения балки, записывая каждый раз отсчеты ![]() по
реохорду.
по
реохорду.
5. Разгрузить балку до начальной нагрузки и проверить отсчет по реохорду.
6. Подключить измеритель деформаций к датчику Т 2 и повторить пункты 3-5.
При обработке результатов
эксперимента определим среднюю разность отсчетов при увеличении нагрузки на ![]() (в отдельности для датчиков Т
1 и Т 2):
(в отдельности для датчиков Т
1 и Т 2):
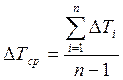 ,
,
где: ![]() ;
; ![]() -
количество отсчетов.
-
количество отсчетов.
Далее вычислим среднюю величину приращения деформаций:
![]() ;
;
![]() ;
;
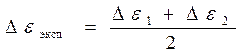 ,
,
где: ![]() и
и ![]() -
тарировочные коэффициенты (указываются преподавателем).
-
тарировочные коэффициенты (указываются преподавателем).
Используя закон Гука, рассчитаем
среднюю величину приращения напряжений при изменении нагрузки на ![]() :
:
![]() ,
,
где ![]() - модуль продольной упругости
материала.
- модуль продольной упругости
материала.
Выполнить теоретический расчет
напряжений в балке от силы ![]() :
:
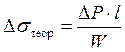 ,
,
где ![]() - момент сопротивления сечений
балки, для круглого сечения:
- момент сопротивления сечений
балки, для круглого сечения:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.