Определение перемещений при косом изгибе. Одновременное действие изгиба и кручения. Ядро сечения

Определение перемещений при косом изгибе.

Полное перемещение при косом изгибе определяется как сумма перемещений в горизонтальном и вертикальном направлении, то есть вертикальная составляющая силы определяет вертикальное перемещение, а горизонтальная составляющая силы - горизонтальное.

   Fy=F*cosφ

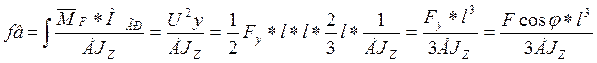
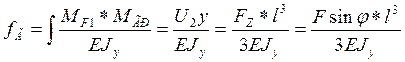
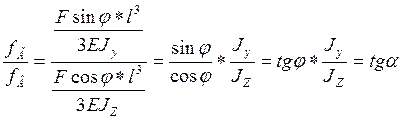
Одновременное действие изгиба и кручения.

Пользуясь принципом жесткости для сил определим отдельно напряжение от изгиба и от кручения.

         

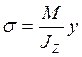
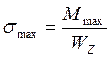
Касательными напряжениями при изгибе пренебрегаем, т.к. они малы посравнению с касательными напряжениями при кручении.

        

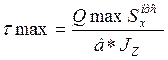
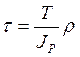
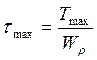
Анализ эпюр внутренних усилий установил, что опасным является сечение в заделке, так как там максимальные M и T.

На площади поперечного сечения проходящего через точку С создается наибольшее касательное напряжение от кручения и нормальное напряжение от игиба.

Из условия прочности подобрать размеры стержня, и допускаемое сечение.

Детали работающие на изгиб с кручением часто встречаются в машиностроении.

Даже прямой вал изгибается собственным весом, и весом шкивов.

Крутящий момент определяется по мощности вала.

Внецентренное д-е нагрузки.

 Внецентренное растяжение(сжатие)-действует параллельно продольной оси, но не совпадает с ней.

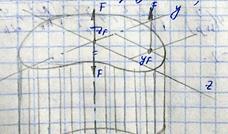
Y_F , Z_F - координаты точки приложения силы

O_Y, O_Z-  главные оси инерции.

Проведем силу в точке тяжести сечения.

σ =N/A= F/A

F- деформация изгиба, так как изгиб не лежит ни в одной плоскости инерции.

σ =M_y/I_y*z+M_z/I_z*y

Y_F >0; Z_F>0.

Определим напряжение в любой точке сечения:

F-Внешняя сила

А-площадь поперечного сечения

Y_F  Z_F-координаты точки приложения силы.

Y,Z-координаты точки, где определяем напряжение.

Условия прочности при внецентренном  действии нагрузки для случая, если  материал одинаково работает на растяжение9сжатие0 имеет вид:

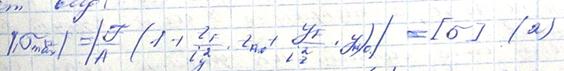
В формуле (2) Z, Y- координаты точек наиболее удаленных от оси.

- (3)-уравнение нейтральной линии при внецентренном действии нагрузки.

Используя формулу (3) можно получить отрезки, j отсекающие нейтральную ось по координатным осям.

Если Z_но=0, то 1+Y_f/i²_z*Y_но=0 ; Y_но= - i²_z / Y_f.

Если Y_но=0, то 1+Z_f/i²_z*Z_но=0 ; Z_но= - i²_z / Z_f/

Для того чтобы найти опасные точки сечения, необходимо провести касательную к сечению, параллельную нейтральной оси. Точки касания и будут опасными точками сечения.

Используя уравнения отрезков, можно построить ядро сечения.

Ядро сечения

Ядро сечения - Область расположенная вокруг центра тяжести сечения.

 Если внешняя нагрузка лежит в области ядра сечения, то напряжения в сечении будут одного знака, а нейтральная линия проходит за сечение.

Если сила лежит вне ядра сечения, то нейтральная линия проходит по сечению, а напряжения в сечениях будут разных знаков.

Если сила лежит на границе сечения, то нейтральная линия является касательной к сечению, и напряжения в сечениях будут одинакового знака.

Используя это свойство, и уравнение (4) , можно построить ядро сечения. Для этого необходимо задавать положение нейтральной оси, таким образом, чтобы она являлась касательной к сечению. Обойдя сечение по контуру, мы получим границы ядра сечения.

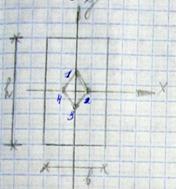
I_y=B³H/12

I_Z=H³B/12

I²_y=B²/12

I²_Z=H²/12

A=H*B

1)  Y_но= - H/2

Z_но=∞

a_y= - I²_Z/ Y_но

a_z= - I²_y/ Z_но

      a_y= - I²_Z/ Y_но= - H²/(12(-H/2))= H/6

 Z=∞  a_z= I²_y/ Z_но=0

2)  Z_но= - B/2

Y_но=∞

      a_Z2= - I²_y/ Z_но= - B²/(12(-B/2))= B/6

 Y=∞  a_y2= I²_Z/ Y_но=0

3)  Y_но= H/2

Z_но=∞  a_y= -H/6 a_z= 0

4)  Z_но= B/2

Y_но=∞

      a_Z= - B/6

a_y= 0