
Этот алгоритм за O(n) операций "выправляет" впуклости многоугольника (замкнутой непересекающейся ломаной из n+1 отрезков), строя таким образом его выпуклую оболочку.
Точки могут поступать по мере выполнения алгоритма, и их количество заранее неизвестно. Главное, чтобы ломаная не пересекалась. Для начала объявим вспомогательную функцию f, которая для любой тройки точек (x, y, z) будет положительна, равна нулю или отрицательна (f > 0, f = 0 или f < 0) в зависимости от того, находится ли z справа, на одной линии или слева от линии (x, y).
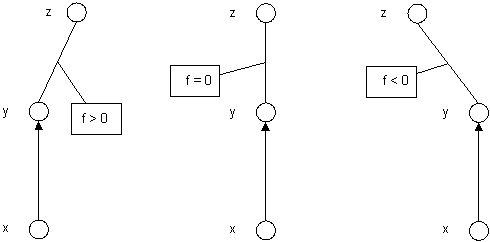
Пусть ломаная задана точками:
v1, ..., vm
Алгоритм начинает с пустого дека D. (Дек - это список с операциями). Рассмотрим следущее множество операций:
· push v - положить элемент на верх дека,
· insert v - положить элемент вниз дека,
· pop - убрать верхний элемент дека,
· remove - удалить нижний элемент дека.
Псевдокод алгоритма может быть записан следующим образом.
Алгоритм
Ввод v1, v2, v3;
if f(v1, v2, v3) > 0
{
push v1; push v2;
}
else
{
push v2; push v1;
}
push v3;
insert v3;
Ввод v;
while (f(v, db, db+1) < 0 or f(dt-1, dt, c) < 0)
Ввод v;
while (f(dt-1, dt, v) > 0)
pop;
push v;
while (f(v, db, db+1) > 0)
remove;
insert v;
Идти на Блок 2;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.